
- •Связь линейных и угловых характеристик движения:
- •2) Инерциальные системы отсчета. Понятия силы и инертной массы. Законы динамики. Силы в природе. Фундаментальные взаимодействия. Свойства сил упругости и тяготения. Свойства сил трения.
- •3) Центр инерции. Закон сохранения импульса системы материальных точек.
- •4) Работа переменной силы. Кинетическая энергия и ее связь с работой внешних и внутренних сил.
- •6) Закон сохранения механической энергии. Диссипация энергии.
- •Работа при вращении твердого тела ()
- •8)Колебания математического и физического маятников.
- •9) Преобразования Галилея. Механический принцип относительности. Нарушение классического закона сложения скоростей. Опыты по определению скорости света. Опыт Майкельсона.
- •11) Статистический и термодинамический методы исследования. Термодинамические параметры. Идеальный газ. Термодинамическая система. Равновесные и неравновесные состояния и процессы.
- •Термодинамические параметры: объём , температура , давление и масса , концентрации составляющих систему веществ , химические потенциалы составляющих веществ , внутренняя энергия , энтропия .
- •12. Среднеквадратичная скорость молекул. Молекулярно-кинетическое толкование абсолютной температуры.
- •13. Основное уравнение молекулярно-кинетической теории (вывод). Число степеней свободы молекулы. Закон распределения энергии по степеням свободы. Внутренняя энергия идеального газа.
- •14. Работа газа при расширении. Количество теплоты. Первое начало термодинамики.
- •15. Классическая молекулярно-кинетическая теория теплоемкости. Удельная и молярная теплоемкости. Формула Майера. Границы применимости теории.
- •Формула Майера ()
- •16. Изопроцессы идеального газа. Зависимость теплоемкости от вида процесса. Адиабатический процесс.
- •17. Тепловые двигатели и холодильные машины. Кпд. Обратимые и необратимые процессы. Круговой процесс. Цикл Карно для идеального газа и его кпд.
- •19. Закон Максвелла для распределения молекул идеального газа по скоростям теплового движения. Вероятностное толкование закона распределения Максвелла.
- •20. Барометрическая формула. Закон Больцмана для распределения частиц идеального газа во внешнем потенциальном поле.
- •Одной молекулы газа
- •Потенцирование:
- •21. Среднее число столкновений и средняя длина свободного пробега молекул идеального газа. Эффективный диаметр молекулы.
- •22. Явления переноса. Теплопроводность, диффузия, вязкость.
- •23. Реальные газы. Силы и потенциальная энергия межмолекулярного взаимодействия. Уравнение Ван-дер-Ваальса. Изотермы реального газа. Критическое состояние. (Внутренняя энергия реального газа.)
- •Уравнение Ван-дер-Ваальса – уравнение, связывающее основные термодинамические величины в модели газа Ван-дер-Ваальса.
19. Закон Максвелла для распределения молекул идеального газа по скоростям теплового движения. Вероятностное толкование закона распределения Максвелла.
Распределение Максвелла – общее наименование нескольких распределений вероятности, которые описывают статистическое поведение параметров частиц идеального газа. Вид соответствующей функции плотности вероятности диктуется тем, какая величина выступает в качестве непрерывной случайной величины.
Закон для распределения молекул
идеального газа по скоростям:

Наиболее вероятная скорость:

Средняя квадратичная скорость:
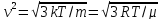
Средняя арифметическая скорость:

Вероятностное толкование закона
Максвелла. Выражение
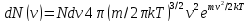 даёт число молекул, величина скоростей
которых лежит в интервале от
даёт число молекул, величина скоростей
которых лежит в интервале от
 до
до
 .
Разделив его на
.
Разделив его на
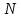 получим вероятность того, что скорость
молекулы окажется между
получим вероятность того, что скорость
молекулы окажется между
 и
и
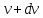 ,
то есть
,
то есть

20. Барометрическая формула. Закон Больцмана для распределения частиц идеального газа во внешнем потенциальном поле.


Если
 ,
то
,
то

Одной молекулы газа
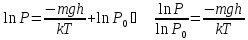
Потенцирование:
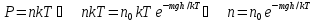
21. Среднее число столкновений и средняя длина свободного пробега молекул идеального газа. Эффективный диаметр молекулы.
Столкновение между одинаковыми молекулами
может произойти только в том случае,
если их центры сблизятся на расстояние,
меньшее или равное диаметру
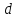 – эффективному диаметру молекулы.
– эффективному диаметру молекулы.
Концентрация

Среднее число столкновений

Учитывая, что все молекулы движутся,

Среднее время между 2 столкновениями
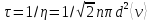
Средняя длина свободного пробега

Эффективный диаметр молекулы ( )
– минимальное расстояние, на которое
сближаются центры двух молекул при
столкновении.
)
– минимальное расстояние, на которое
сближаются центры двух молекул при
столкновении.
22. Явления переноса. Теплопроводность, диффузия, вязкость.
Явления переноса – необратимые процессы в неравновесных системах, в результате которых происходит пространственный перенос массы, энергии или импульса.
Теплопроводность [Вт/м*К] – способность материальных тел проводить энергию (теплоту) от более нагретых частей тела к менее нагретым частям тела путём хаотического движения частиц тела. Эта характеристика равна количеству теплоты, проходящему через однородный образец материала единичной длины и единичной площади за единицу времени при единичной разнице температур.
Количественно теплопроводность
подчиняется закону Фурье:
 ,
где
,
где
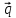 – вектор плотности теплового потока
– количество энергии, проходящей в
единицу времени через единицу площади,
перпендикулярной оси
– вектор плотности теплового потока
– количество энергии, проходящей в
единицу времени через единицу площади,
перпендикулярной оси
 ,
,
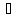 – коэффициент теплопроводности,
– коэффициент теплопроводности,
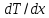 – градиент температуры в направлении
– градиент температуры в направлении
 .
.
Диффузия ( )
– процесс взаимного проникновения
молекул одного вещества между молекулами
другого вещества, приводящий к
самопроизвольному выравниванию их
концентраций по всему занимаемому
объёму. Диффузия происходит в направлении
падения концентрации вещества.
)
– процесс взаимного проникновения
молекул одного вещества между молекулами
другого вещества, приводящий к
самопроизвольному выравниванию их
концентраций по всему занимаемому
объёму. Диффузия происходит в направлении
падения концентрации вещества.
Явление диффузии для химически однородного
газа подчиняется закону Фика:
 ,
где
,
где
 – плотность потока массы – величина,
определяемая массой вещества,
диффундирующего в единицу времени через
единичную площадку, перпендикулярную
оси
– плотность потока массы – величина,
определяемая массой вещества,
диффундирующего в единицу времени через
единичную площадку, перпендикулярную
оси
 ,
,
 – коэффициент диффузии,
– коэффициент диффузии,
 – градиент плотности газа в направлении
– градиент плотности газа в направлении
 .
.
Вязкость ( )
[Па*с] – свойство текучих и твёрдых тел
оказывать сопротивление перемещению
одной их части относительно другой.
Механизм внутреннего трения в жидкостях
и газах заключается в том, что хаотически
движущиеся молекулы переносят импульс
из одного слоя в другой, что приводит к
выравниванию скоростей. Вязкость
характеризуют интенсивностью работы,
затрачиваемой на осуществление течения
газа или жидкости с определенной
скоростью.
)
[Па*с] – свойство текучих и твёрдых тел
оказывать сопротивление перемещению
одной их части относительно другой.
Механизм внутреннего трения в жидкостях
и газах заключается в том, что хаотически
движущиеся молекулы переносят импульс
из одного слоя в другой, что приводит к
выравниванию скоростей. Вязкость
характеризуют интенсивностью работы,
затрачиваемой на осуществление течения
газа или жидкости с определенной
скоростью.
Закон Ньютона для внутреннего трения
можно представить в виде:
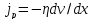 ,
где
,
где
 – плотность потока импульса – величина,
определяемая импульсом, переносимым в
единицу времени через единичную площадку
соприкосновения слоев жидкости или
газа в направлении оси
– плотность потока импульса – величина,
определяемая импульсом, переносимым в
единицу времени через единичную площадку
соприкосновения слоев жидкости или
газа в направлении оси
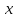 ,
перпендикулярном направлению движения
слоев жидкости или газа,
,
перпендикулярном направлению движения
слоев жидкости или газа,
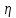 – коэффициент динамической вязкости
газа,
– коэффициент динамической вязкости
газа,
 – градиент температуры в направлении
– градиент температуры в направлении
 .
.
