9.3. Построение профиля
При построении профиля с плана следует перенести расстояния между горизонталями на прямую линию, принятую за нулевую, отметив их точками (рис. 53). Затем от этих точек вверх по перпендикулярам отсчитать высотные отметки горизонталей. Соединив эти точки, получим профиль.
При построении профиля необходимо указывать линейный масштаб горизонтальной и вертикальной шкалой. Указать стрелками местонахождение реки, озера и исследуемого объекта.
10. Глазомерная съемка местности
Глазомерной называется такая съемка, при которой план местности можно получить с помощью самых простых измерений при наименьших затратах времени. Такая съемка применяется в тех случаях, когда не требуется большой точности, при предварительных изысканиях и разведках.
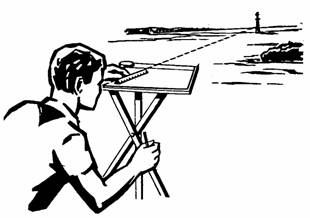
Рис. 54. Визирование линейкой
Главные требования, предъявляемые к глазомерной съемке – быстрота, ясность и наглядность.
Быстрота достигается применением простейших способов измерения длин и углов (рис. 54). Ясность и наглядность достигаются применением отчетливых и стандартных условных знаков, выделением основных ориентиров и особенностей местности.
Глазомерную съемку хорошо может выполнить только съемщик, у которого имеется навык достаточно верно оценивать на глаз расстояния и углы, т.е. достаточный опыт во всех видах съемочных работ.
Навык глазомерной оценки расстояния вырабатывается со временем, в течение которого съемщик занимается измерением длин мерной рулеткой.
10.1. Измерение длин
При глазомерной съемке расстояния можно определять также шагами и на особо дальних расстояниях (например, в пешем маршруте) по времени. Кроме того, можно пользоваться стандартными расстояниями, принятыми при строительстве линий электропередач между столбами и опорами ЛЭП. Так между столбами ЛЭП-220-250 высотой 6 м расстояние соблюдается равным 50 м. Между опорами высоковольтных ЛЭП соблюдается расстояние в 150 м. Следует помнить, что между столбами ЛЭП-220 высотой 8-10 м иногда соблюдается расстояние больше 50 м.
При съемке обычно считают пары шагов. На небольших расстояниях, однако, можно считать каждый шаг. Для определения расстояний шагами необходимо знать среднюю длину своего шага, для чего промеривают несколько раз какие-либо замеренные расстояния, например 100 м. Допустим, в 100 м в среднем получается 120 шагов. Значит, длина шага будет 100 : 120 = 0,83 м. Нужно иметь в виду, что при подъемах и спусках средняя длина шага уменьшается.
Крутизна подъема или спуска |
% уменьшения длины |
|
100 200 300 |
20 35 50 |
5 15 35 |
Длина шага зависит также от грунта. Например, при ходьбе по сухому сыпучему песку длина шага уменьшается примерно на 10 %, по траве – на 3-7 %.
11. Определение высот и неприступных расстояний
Иногда возникает необходимость определения неприступного расстояния, например, ширину оврага, лощины, ручья, речки и т.д. В этом случае измерения можно провести простейшими инструментами и приемами. Для этого необходимы компас и два шеста или колышка. Наиболее простой способ при нешироких расстояниях заключен в использовании теоремы равенств катетов прямоугольного равнобедренного треугольника.
Для получения расстояния от точки А до точки В необходимо найти положение точки С (рис. 55). Для чего от точки А, перпендикулярно к линии АВ, намечают линию АС, где в точке С образован угол в 450 к точке В (угол АСВ).
П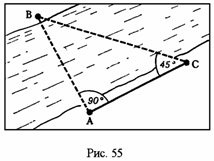
олученный
таким образом отрезок АС явится стороной
(катетом) равнобедренного треугольника
АВС и будет равен искомой стороне АВ,
которую теперь будет легко измерить.
Другой способ измерения заключается в использовании теоремы тангенсов прямоугольного треугольника b=c tgB (рис. 56). Для этого, кроме компаса необходимо иметь под рукой таблицу Брадиса, если изображение плана решено сделать в поле. В противном случае можно ограничиться схематической зарисовкой и записанными углами и расстоянием короткой стороны треугольника.
Д
ля
упрощения этой задачи делается выписка
тангенсов некоторых заданных углов,
например tg 600, 650, 700,
750. Тогда по линии АВ от точки А
надо пройти до тех пор, пока не образуется
какой-либо из выбранных углов (например
650) при визировании на точку С.
Для определения высот террас, скальных уступов и пр. также можно прибегнуть к теореме синусов или косинусов прямоугольного треугольника b=a sinB, b=a cosC (рис. 57), либо b=c tgB.
Углы В и С измеряются транспортиром с отвесом или горным компасом. Решение задачи здесь осложняется измерением линии а (ВС) (длинной стороны треугольника – гипотенузы). Измерение линии ВС можно произвести рулеткой при пологих склонах или невысоких обрывистых террасах, или нивелиром с помощью дальномерных нитей. Нивелир при этом придется держать в руках, облокотив его на шест или на что-нибудь неподвижное, т.к., держа его просто на руках, невозможно будет сделать отсчет из-за колебаний изображения. Рейкой можно попытаться подловить угол визирования, приложив к ней прямоугольный треугольник или транспортир (горный компас) и свизировав их на съемщика. Можно рейку держать строго вертикально. Тогда при вычислениях необходимо сделать поправку на искажение отсчета расстояния через косинус угла В: а=n cosB, где n= искаженный отсчет расстояния ВС.
Расстояние ВС можно получить способом засечки точки С с точек А и В, как это описано для рисунка 56, здесь ВС (рис. 57) = АС (рис. 56). Следующим действием будет решение уравнения по теореме синусов или косинусов, описанное выше для рисунка 57.
Высоту террасы можно определить и сравнительным способом, сравнивая ее с высотой деревьев, столбов ЛЭП и т.д. Высоту дерева, растущего у подножия террасы, можно определить с помощью транспортира с отвесом или горным компасом, используя свойства равнобедренного треугольника, где стороны катетов равны друг другу (рис. 58).
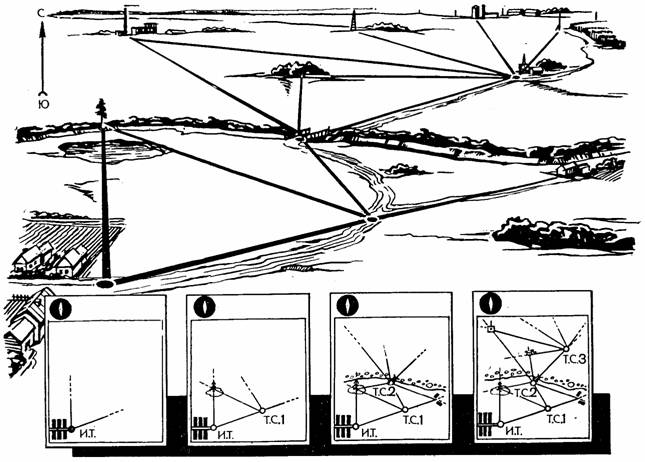
Рис. 59. Схема составления плана глазомерной съемки