6.2 Определение оптимальных значений параметров настройки регуляторов каскадной системы управления

Аналогично как для одноконтурной системы воспользуемся системой [2] для определения настроечных параметров:

(54)

где - обратная передаточная функция эквивалентного объекта (24),

(55)

-действительная и мнимая части передаточной функции эквивалентного объекта.

Для получения расширенных частотных характеристик сделаем подстановку

s= - m + j в выражение (55):

Воспользуемся формулой Эйлера, преобразуем уравнение:

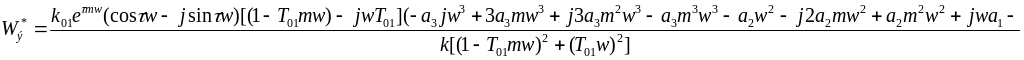
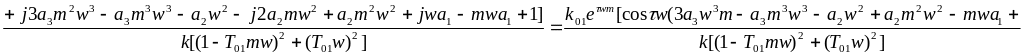
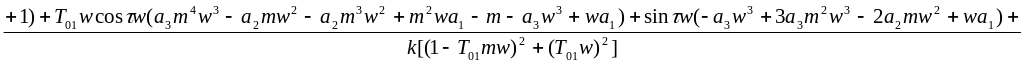
Из полученного выражения выделим мнимую и действительную часть:

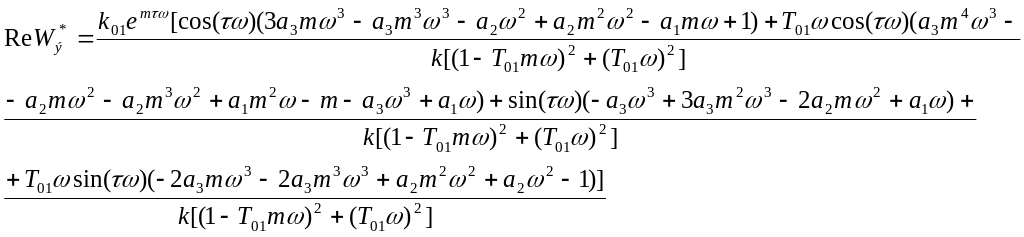
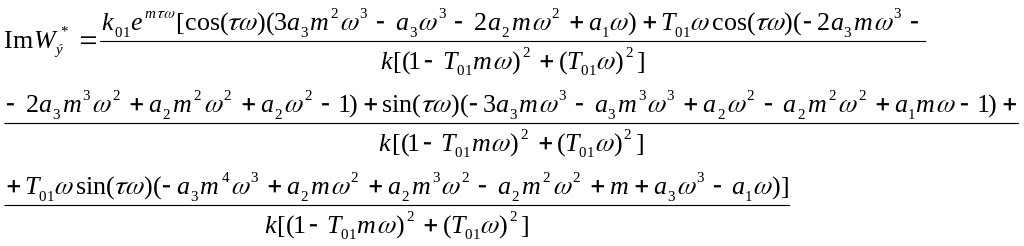
Подставляя числовые значения в выражения мнимой и действительной части эквивалентного объекта, получим:

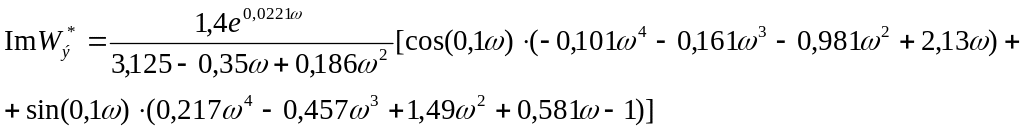
Подставим найденные выражения и m=0,221 в систему (52).

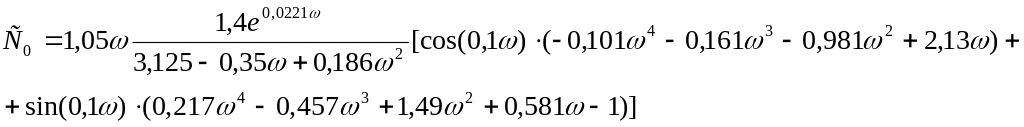(56)

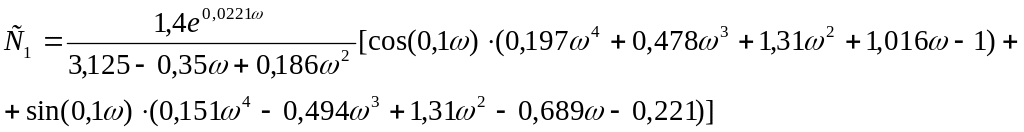(57)

Используя (56) и (57) построим зависимость С₀(С₁):

Таблица 7.

w	C0	C1
0	0	-0,448
0,1	0,009182	-0,4032
0,2	0,035209	-0,3462
0,3	0,075664	-0,27752
0,4	0,127877	-0,19762
0,5	0,188857	-0,10685
0,6	0,255223	-0,00548
0,7	0,323145	0,10636
0,8	0,388285	0,228655
0,9	0,44575	0,361553
1	0,490053	0,505358
1,1	0,515071	0,660539
1,2	0,514025	0,827735
1,3	0,479462	1,007753
1,32	0,467822	1,045378
1,4	0,403238	1,201567
1,5	0,276527	1,41031
1,6	0,089828	1,635264
1,65	-0,02917	1,754259

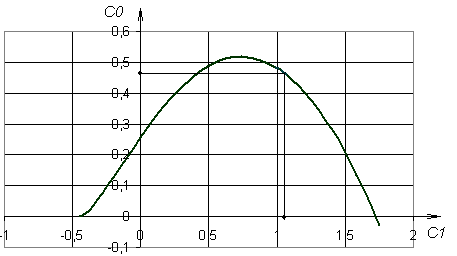
Рис. 18. Кривая оптимальных настроек ПИ-регулятора каскадной системы

Выбираем параметры настройки регулятора на частоте , .

, ;

.

. (58)

Настройки П-регулятора будут определяться выражением:

(59)

Воспользуемся выражением (26):

(60)

Подставим s = -m + j в выражение (60) и получим:

Выделим вещественную часть

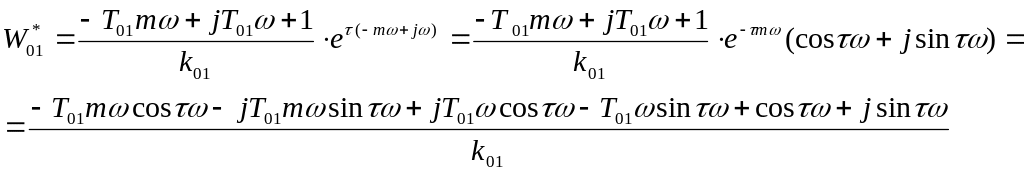
(61)

При m=0,221

(62)

При m=0

(63)

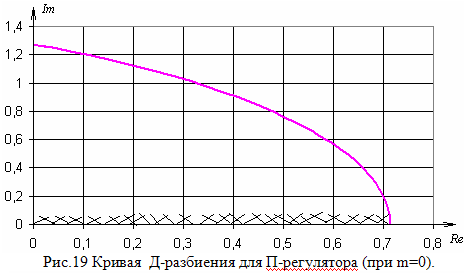
По найденным выражениям строим кривую Д-разбиения и кривую оптимальной настройки П-регулятора.

Таблица 8.

Значения П-регулятора могут изменяться в пределах

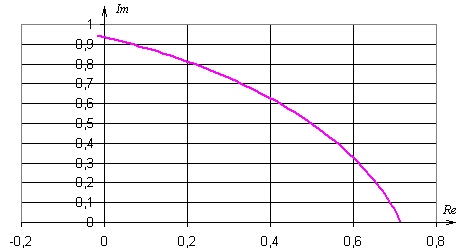
Рис.20. Кривая настройки П-регулятора (при m=0,221).

Выбираем параметр настройки П-регулятора:

(64)