5. Определение условий устойчивости системы

При исследовании системы важно определить пределы, в которых могут быть изменены те или иные параметры для сохранения устойчивости ее работы. Наиболее удобно производить выделение областей устойчивости на основе понятия о Д-разбиении [2].

5.1. Расчет устойчивости одноконтурной системы

Для определения устойчивости системы нам необходимо характеристическое уравнение одноконтурной системы (14), для этого выпишем его:

(29)

Параметры и входят в уравнение (29) линейно, тогда приведем его к виду:

, т.е. (30)

(31)

Подставляя в уравнение (30) s=jω, получим выражение для границы Д – разбиения

, т.е. (32)

(33)

где

Выделим из уравнения (32) вещественную и мнимую части, приравняв их отдельно к нулю.

(34)

Решение системы (34) имеет вид:

; , (35)

где

С учетом сделанных расчетов параметры С₀ и С₁ будут определяться следующим образом:

(36)

(37)

Задаваясь значениями ω от 0 до ∞ строим границу Д – разбиения в плоскости параметров С₀ и С₁ (Рис.14). Расчетные данные приведены в Таблице 3.

Построим особые прямые при частоте ω=0 , тогда С₀= 0, С₁=-0,32.

Граница Д – разбиения штрихуется слева, если при изменении ω от -∞ до +∞ главный определитель >0, и справа, если <0. В данном случае >0, так как частота ω изменяется в пределах от 0 до +∞. При изменении ω от -∞ до +∞ мы обходим кривую Д – разбиения два раза и поэтому она штрихуется всегда двойной штриховкой.

Штриховка особых прямых производится так, чтобы вблизи точки сопряжения особой прямой и кривой Д – разбиения, заштрихованные и не заштрихованные стороны прямой и кривой были направлены друг к другу.

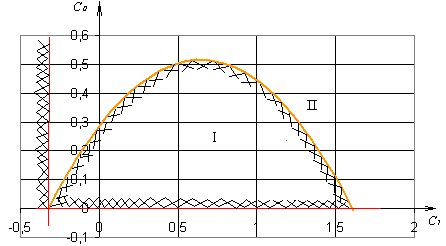
Рис.14. Кривая Д-разбиения для одноконтурной системы

Таблица 3.

0	0	-0,32
0,1	0,007572	-0,3129
0,2	0,029952	-0,2916
0,3	0,066132	-0,2561
0,4	0,114432	-0,2064
0,5	0,1725	-0,1425
0,6	0,237312	-0,0644
0,7	0,305172	0,0279
0,8	0,371712	0,1344
0,9	0,431892	0,2551
1	0,48	0,39
1,1	0,509652	0,5391
1,2	0,513792	0,7024
1,3	0,484692	0,8799
1,4	0,413952	1,0716
1,5	0,2925	1,2775
1,6	0,110592	1,4976
1,65	-0,00626	1,612975

Пусть в области I будет r левых корней, тогда при переходе из во область происходит потеря одного корня (При переходе слева на право мы теряем корень, а с право налево приобретаем.). Следовательно, область I c наибольшим числом левых корней. Проверим найденную область на устойчивость с помощью критерия Рауса-Гурвица. Чтобы проверить действительно эта область является областью устойчивости, зададимся ранее найденными значениями , лежащими в этой области.

Подставим значения в характеристическое уравнение (27) и преобразуем его.

После преобразования получаем

Введем обозначения:

По коэффициентам характеристического уравнения составим определитель

Согласно критерию Рауса – Гурвица для того, чтобы система автоматического управления была устойчива, необходимо и достаточно, чтобы все определители были положительны.

Найденная область устойчива, так как все диагональные миноры положительны. Следовательно, пределы, в которых параметры ПИ-регулятора могут быть изменены для сохранения устойчивости системы, лежат в интервале:

,