4. Выбор регуляторов и математическое описание системы управления

Задача настройки регулятора состоит в том, чтобы, располагая динамическими характеристиками объекта и регулятора, так выбрать и установить настроечные параметры регулятора, чтобы обеспечить оптимальный переходный процесс в автоматической системе.

Под оптимальными настройками регулятора будем понимать настройки, обеспечивающие для заданного объекта процесс регулирования, удовлетворяющий выбранным критериям качества.

Для коррекции динамических свойств системы применяются: пропорциональный (П), интегрирующий (И), пропорционально-интегрирующий (ПИ), пропорционально - интегрально-дифференциальный (ПИД) и пропорционально-дифференциальный (ПД) регуляторы.

Для регулирования температуры низы колонны, с помощью одноконтурной системы управления, будем использовать ПИ – регулятор.

Статическая ошибка у ПИ-регуляторов практически равна нулю, т.е. повышается точность регулирования. Также ПИ-регуляторы обладают достаточным быстродействием и дают возможность вывода параметра на заданный уровень.

У ПИ-регуляторов воздействие входной величины на выход тем больше, чем больше коэффициент пропорциональности и меньше постоянная интегрирования .

Уравнение динамики ПИ-регулятора:

.

Передаточная функция:

, где . (10)

Схема одноконтурной системы управления представлена на рисунке 11.

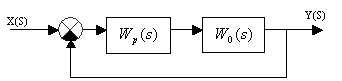
Рис. 11. Одноконтурная система управления

Где - передаточная функция объекта управления

(11)

- передаточная функция ПИ- регулятора (10)

Тогда передаточная функция разомкнутой системы будет иметь вид:

(12)

Передаточная функция замкнутой системы имеет вид:

(13)

Выпишем характеристическое уравнение системы:

(14)

Для каскадной системы управления выбираем регуляторы П-ПИ – первый регулятор является стабилизирующим, а второй корректирующим. Эти регуляторы были выбраны благодаря ряду преимуществ. Колонна ректификации является инерционным объектом, поэтому необходимы регуляторы, которые отличаются быстродействием и работоспособностью на таких объектах, таким свойствами обладают П-регуляторы. Однако использование П-регуляторов возможно при допущении остаточного отклонения параметра от заданного. Автоматические регуляторы с пропорционально-интегральным законом регулирования объединили преимущества П- и И-регуляторов.

У регуляторов с пропорциональным законом регулирования выходная величина в пределах зоны регулирования изменяется пропорционально изменению входа.

Уравнение динамики П-регулятора:

,

где коэффициент пропорциональности.

Передаточная функция П-регулятора, равная отношению выходной величины к входной имеет вид:

.

Передаточная функция ПИ- регулятора (10):

, где .

Схема каскадной системы управления представлена на рисунке 12.

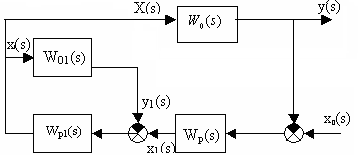
Рис. 12. Каскадная система управления

W₀ (s) - передаточная функция объекта в основном контуре

W₀₁(s) - передаточная функция объекта в вспомогательном контуре

W_p1(s) - передаточная функция стабилизирующего регулятора

W_p(s) – передаточная функция корректирующего регулятора.

Регуляторы по стабилизирующему и по корректирующему контуру имеют разный вид и разные значения параметров настройки.

Корректирующий регулятор:

(15)

Стабилизирующий регулятор:

(16)

Составим следующую систему уравнений:

(17)

Из системы уравнений (17) исключаем промежуточные координаты Y₁(s) и X(s), получим:

(18)

В результате преобразований получаем передаточную функцию эквивалентного объекта включающего стабилизирующий контур:

(19)

Предполагая, что стабилизирующий регулятор практически успевает отслеживать вспомогательную величину y₁ в соответствии с поступающим на него заданием x, т.е., что , тогда передаточная функция эквивалентного объекта управления будет иметь вид:

(20)

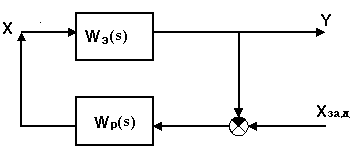
Рис.13. Одноконтурная система регулирования.

Передаточная функция разомкнутой системы, представленной на рис.13, равна:

(21)

Передаточная функция замкнутой системы:

(22)

Следовательно, характеристическое уравнение будет иметь вид:

(23)

(24)

Используя передаточную функцию разомкнутой системы, рассчитаем параметры настройки корректирующего регулятора, т.е. определим передаточную функцию W_р(s). Из уравнения (21) определяем:

(25)

С учетом уравнения (20) получаем:

(26)

Для определения настроек П - регулятора передаточная функция эквивалентного объекта имеет вид:

(27)

Величина не оказывает значительного влияния и его можно не принимать во внимание, тогда:

Воспользовавшись выражением (25) можно записать:

(28)