3.Математическое описание объекта управления.

Математическое описание объекта управления заключается в нахождении передаточной функции объекта управления.

Для определения математического описания объекта воспользуемся методом площадей, предложенным М.П. Симою[2]. Определение математической модели, возможно, произвести с использованием кривой разгона. В основе метода лежит предположение, что исследуемый объект может быть описан линейным дифференциальным уравнением с постоянными коэффициентами:

(1)

где,

– постоянные коэффициенты;

- приведенное к единице отклонение

- приведенное к единице возмущающее воздействие в безразмерном виде.

Рассмотрим заданную кривую разгона.

Рис.6. Исходная кривая разгона с приведенными значениями по оси ординат.

Так как значение регулируемой величины и ее первая производная при t = 0 равны нулю, то в передаточной функции порядок числителя, по крайней мере меньше порядка знаменателя на две единицы. С учетом этого передаточная функция объекта будит иметь вид:

(2)

где

Задача состоит в том, чтобы определить неизвестные коэффициенты.

Перед тем как преступить к определению коэффициентов передаточной функции, необходимо выполнить следующие предварительные преобразования:

1. ось времени разбить на n равных интервалов по ∆t (в нашем случае ось времени разбита на 26 интервалов по ∆t = 14с);

2. по оси ординат откладываются приведенные значения ординат соответствующих точек, т.е. по оси ординат откладывается величина

;

Таблица 1.

3. график кривой разгона перестраивается таким образом, чтобы он умещался в квадрат образованный линиями сетки графика.

Коэффициенты определяются из следующей системы уравнений:

(3)

С учетом выражения (2) система уравнений (3) преобразуется к виду:

(4)

(5)

Входящие в эту систему уравнений коэффициенты _{F1 , F2 , F3 определяются по следующим формулам:}

(6)

(7)

_{В формулах (5) – (7):}

3.1. Математическое описание объекта управления с помощью программы rkpf.

Для нахождения математического описания объекта управления по заданной кривой разгона воспользуемся программой RKPF , которая значительно облегчает задачу. Алгоритм этой программы основан на определении коэффициентов передаточной функции с помощью метода площадей, описанного выше.

Для этого:

1. При запуске программы необходимо указать входные значения в появившемся диалоговом окне:

Выбираем процесс с самовыравниванием.

Рис.7.

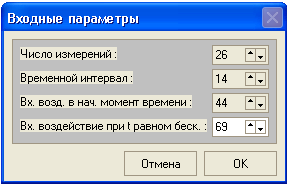
Рис.8.

В данном опыте показания снимались 26 раз с интервалом времени в 14 сек. Ступенчатое входное воздействие, вызвавшее переходный процесс, подавалось изменением температуры от 44 до 69 .

После ввода входных параметров нажмем кнопку «ОК».

Ось времени разбита на равные интервалы с шагом 14 сек, введем в таблицу значения входного сигнала соответствующего каждому интервалу времени.

Рис.9.

После ввода последнего снятого значения загорится кнопка "Вычислить" (зелёный треугольник на панели инструментов) на который необходимо нажать для получения результата.

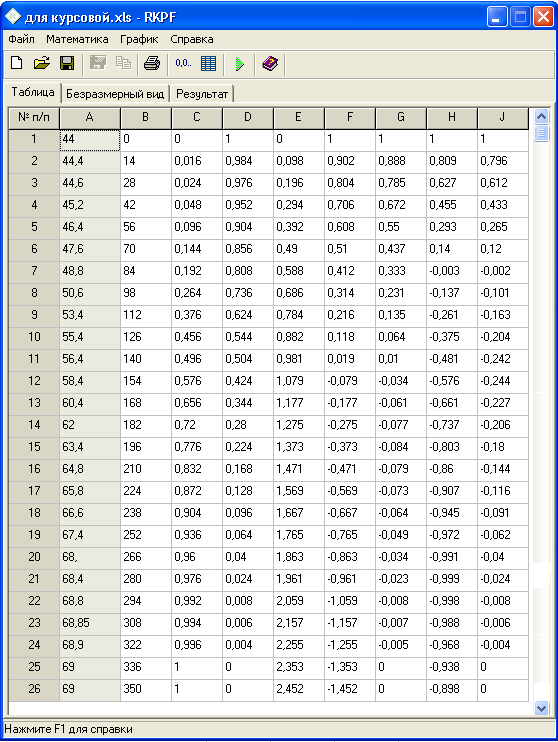
Результат будет Вам представлен в следующем виде:

– таблица вычислений (таблица 2.);

Где:

A – x_вых , значения снятой экспериментальной кривой;

B – t , временной интервал (шаг квантования по времени);

С –  , приведённое к единице отклонение регулируемой величины в

безразмерном виде;

D – (1 – );

E –  = t /F₁;

F – (1 – );

G – (1 – )(1 – );

H – 1 – 2 +  ²/2;

J – (1 – )(1 – 2 +  ²/2).

Таблица 2.

– график кривой разгона в безразмерном виде (синяя - построена по введённым в таблицу значениям, коричневая - построена по найденной передаточной функции);

_Рис.10.

_{Тогда передаточная функция объекта в корректирующем контуре запишется в виде}

(8)

где

_{Коэффициенты передаточной функции:}

Так же как и при любой аппроксимации необходимо определить ошибку:

Согласно техническому заданию передаточная функция объекта в стабилизирующем контуре равна:

(9)

где

• 1,4 мин^-1

• 15 с =0,25 мин

• 6 с =0,1 мин