2.3. Определение сил трения и количества теплоты, выделяющейся при трении

При контактно-гидродинамическом расчете подшипника, зубчатой передачи и т.п. необходимо вычислять коэффициент трения и количество теплоты в смазочном слое. Без этих данных невозможно определить среднеинтегральное значение вязкости масла.

Определим коэффициент трения. Как известно, касательное напряже­ние в смазочном слое

Согласно [1]

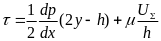(2.15)

Примем, что касательное напряжение, возникающее в какой-либо по­верхности трения, является положительным, если оно направлено в сторону роста координаты х. Тогда касательное напряжение, возникающее в ведушей поверхности, где у = О,

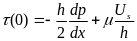
Для определения касательного напряжения, возникающего в ведомой поверхности, обратим внимание на то, что при по формуле (15) опре­деляется напряжение в данном элементе смазочного слоя лежащими вы­ше слоями или верхней поверхностью трения. Касательное же напряжение в верхней поверхности имеет противоположный знак. Отсюда

Перейдя от размерных величин к безразмерным и подставив вместо 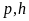и соответствующие значения, получим

(2.16)

Общие силы трения, действующие на единицу длины соответствующей поверхности,

Cледовательно,

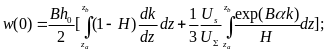
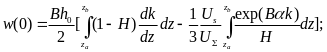(2.17)

Рис 2.4. Зависимости F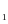 от параметра при различных

значениях С

Следует заметить, что вместо введено . Такая замена допустима, так как она приводит после интегрирования к появлению дополнительных членов и 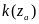, которые равны нулю.

Вместе с тем подынтегральное выражение имеет различные знаки при изменении аргумента вдоль области трения. При вычислении такого интеграла теряется точность расчета. При интегрировании же подынтегральное выражение всегда положительно, что резко повышает точность расчетов.

Введя обозначения:

F = ; (2.18)

получим

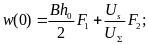
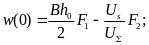(2.19)

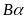Значения при разных С и приведены на рис. 2.4. Приближенное F 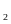может быть вычислено следующим образом. Учтем, что почти во всей области трения 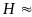1 и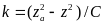 . При этом значительные давления распределяются по почти симметричной площадке протяжённостью от - z до z . Тогда

При 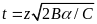получим

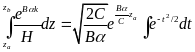
Приняв 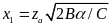и обозначив интеграл вероятности через 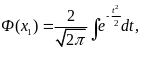получим

Почти во всех случаях реальных комбинаций параметров С и B интеграл вероятности отличается от единицы столь мало, что можно принять с погрешностью 1….2%.

Тогда

(2.20)

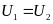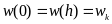Напомним, что при чистом качении и , а , следовательно,

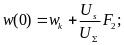
(2.21)

Коэффициент трения на поверхности

(2.22)

При чистом качении 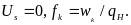Таким образом,

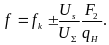(2.23)

Если заданы скорости движения 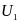и 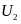, то по формулам (2.27) и (2.28) можно вычислить коэффициент трения и общие силы трения, приложенные поверхностям трения.

Если же одна поверхность приводится в движение, а другая движется только вследствие действия на нее сил трения, т.е. имеет место фрикционное качение, и к ведомой поверхности не приложено никаких сил сопротивления, то окружная сила трения w(h) равна нулю.

Следовательно,

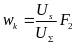
Таким образом, коэффициент трения при фрикционном качении равен удвоенному , т.е.

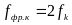(2.24)

Коэффициент проскальзывания при фрикционном качении

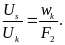(2.25)

При наличии сил сопротивления, приложенных к ведомой поверхности, значительно возрастает коэффициент трения, который зависит от степени проскальзывания поверхностей трения, и трение в смазочном слое уже нельзя считать изотермическим процессом.

Определим количество теплоты, выделяющейся в смазочном слое при трении. Согласно [1] количество теплоты в элементарном объеме ньютоновского смазочного материала можно представить в виде

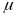- вязкость масла в данной точке при средней температуре области трения и местном давлении р.

После интегрирования получим выражение для определения количества теплоты, выделяющейся в области трения в единицу времени:

Подставив сюда 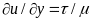и в соответствии с формулой (2.15), получим

Откуда

Перейдем от размерных параметров к безразмерным:

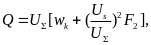(2.26)

Последнее выражение можно получить и через силы трения, действующие на поверхностях трения:

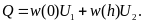(2.27)