4.2. Определение вероятности проявления последствий

проскальзывания

Как установлено в результате теоретических и экспериментальных исследований, последствия проскальзывания быстроходного роликового подшипника проявляются при одновременном выполнении следующих условий:

С помощью номограммы (рис. 4.2) можно рассчитать число тел качения в зоне нагружения подшип­ника без учета центробежных сил и определить вероятность проявления последствий проскальзывания.

Для пояснения на рис. 4.2 пунк­тирными линиями показано, как определять минимальное число тел качения.

На нижней вертикальной оси ординат откладывается отношение g/ , где g – рабочий или (что значительно хуже) монтажный радиальный зазор, , мкм; — нагрузка на единицу длины ролика; ,где - радиальная нагрузка на подшипник Н; , - рабочая длина ролика, мм.

На левой оси абсцисс левого верхнего квадранта получаем наименьшее число тел качения в зоне нагружения. Например, если угол зоны нагружения равен 2 , где — угол между двумя соседними роликами, то в этой зоне находятся три ролика. При этом нагрузка на крайние ролики равна нулю. Таким образом, наименьшее число нагруженных роликов

Рис. 4.2. Номограмма для определения числа тел качения в зоне нагружения .

1)

2) нахождение в рабочей зоне подшипника трех и меньше тел качения.

4.3. Основы контактно-гидродинамического расчета долговечности роликоподшипников

Долговечность подшипников качения может быть повышена в 2 ... 8 раз за счет увеличения вязкости смазочного материала, а следовательно, и тол-шина смазочного слоя.

Для проверки этой зависимости Д.С. Кодниром, Б.А. Куликовым и А.М. Пиковским была экспериментально определена долговечность трех партий по 20 роликовых подшипников В32212ДТ2 в каждой, изготовлен­ных из стали одной плавки, работающих в одном и том же режиме,но при различной толщине смазочного слоя, что было достигнуто применением трех различных смазочных материалов: масла индустриального И-12А, смеси масел МС-20 (25 %) и трансформаторного (75 %), смеси масел МС-20 (50 %) и трансформаторного (50 %).

Подшипники испытывали под радиальной нагрузкой = 19,23 кН при вращении внутреннего кольца с частотой n = 5000 мин . Вычисленная при этом по [6] долговечность , составляла 50 ч. Во время испытаний фиксировали температуры наружного кольца подшипника и масла на вхо­де в подшипник, а также температуру окружающего воздуха; контролиро­вали стабильность нагрузки и частоту вращения вала.

Для каждой партии подшипников определяли действительную долго­вечность при 90 %-ной надежности по Вейбуллу и рассчитывали толщи­ну смазочного слоя по приведенной ранее методике. В результате обработ­ки экспериментальных данных обнаружено, что небольшое изменение со­держания компонентов в смеси масел, влияющее на ее вязкость и толщину смазочного слоя, существенно (в несколько раз) изменяет долговечность подшипника.

Для получения количественной связи между толщиной смазочного слоя и долговечностью были обработаны результаты стендовых испытаний на долговечность более чем 2000 подшипников. После теоретических рас­четов предложена следующая формула для определения действительной долговечности быстроходных радиальных роликоподшипников при 90, 98 и 99 %-ной надежности

Где - коэффициент, учитывающий влияние толщины смазочного слоя на долговечность;

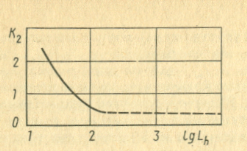
Рис. 4.3. Зависимость коэффициента от расчетной долговечности

К — коэффициент, учитывающий ужесточение режима испытания (определяется по рис. 4.3); , - расчетная долговечность, опре­деляемая по общепринятой методике при 90 %-ной надежности.

Коэффициент определяем по формулам:

при 90 %-ной надежности К = 44,75 — 7,5/ ;

при 98 %-ной надежности К = 20,0 - 3,41/ ;

при 99%-ной надежности К = 15,0 - 2,59 ;

здесь — толщина смазочного слоя, мкм, определяемая по формуле (1.19).

Пример. Исходные данные: роликовый подшипник 5АВ32118Б2Т2 (опора ротора турбины) смазывается смесью из 25 % масла МС-20 и 75 % трансформаторного масла. Геометрические параметры: = 90 X 140 X 24; диаметр ролика = 0,012 м; рабочая длина ролика = 0,01 м; число роликов Z = 22; радиальная нагрузка Рг = = 3,15 кН; частота вращения внутреннего кольца подшипника n = 15 100 мин ; дина­мический коэффициент К - 1,2; реальная рабочая температура Т = 160 °С ( = 0,00188 Паּс; = 0,57ּ10 Па ).

Решение. При коэффициенте долговечности С = 61,3 кН определим

Найдем нагрузку на единицу длины линии контакта: = 72,3 кН/м; приведен­ный радиус кривизны = 5376 мм.

Определим = 11 950 ч.

Найдем нагрузку на единицу длины линии контакта: = 72,3 кН/м; приведен­ный радиус кривизны = 5376 мм. Определим суммарную скорость: = 88,9 м/с; = 0,218 мкм.

Для вычисления действительной долговечности найдем К (90 %) = 10.3; К (98%) =4,37; К (99%) =3,14.

Затем на рис. 4.3 найдем К = 0,28. Тогда для 90, 98 и 99 %-ной надежности 34 450 ч; = 14 630 ч; = 10 500ч.Эти значения весьма близки к полученным при эксплуатации.