Способы определения координат центра тяжести

Исходя из полученных ранее общих формул, можно указать способы определения координат центров тяжести твердых тел:

1 Аналитический (путем интегрирования).

2 Метод симметрии. Если тело имеет плоскость, ось или центр симметрии, то его центр тяжести лежит соответственно в плоскости симметрии, оси симметрии или в центре симметрии.

3 Экспериментальный (метод подвешивания тела).

4 Разбиение. Тело разбивается на конечное число частей, для каждой из которых положение центра тяжести C  и площадь  S известны. Например, проекцию тела на плоскость xOy  (рисунок 1.8) можно представить в виде двух плоских фигур с площадями S₁  и  S₂ (S = S₁ + S₂). Центры тяжести этих фигур находятся в точках  C₁(x₁, y₁) и  C₂(x₂, y₂). Тогда координаты центра тяжести тела равны

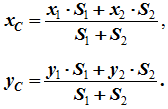
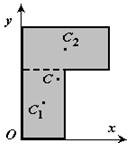
Рисунок 1.8

5 Дополнение (метод отрицательных площадей или объемов). Частный случай способа разбиения. Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны. Например, необходимо найти координаты центра тяжести плоской фигуры (рисунок 1.9):

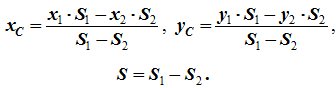
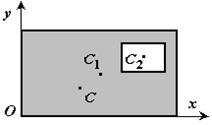
Рисунок 1.9

Тема 2. Связи и их реакции

    Тело, которое может совершать из данного положения любые перемещения в пространстве, называется свободным.

    Тело, перемещениям которого препятствуют какие-нибудь другие, скрепленные или соприкасающиеся с ним тела, называется несвободным. Все то, что ограничивает перемещение данного тела, называют связью.

    Сила, с которой данная связь действует на тело, препятствующая тем или иным его перемещениям, называется реакцией связи. Реакция связи направлена в сторону противоположную той, куда связь не дает перемещаться телу.

    Принцип освобождаемости от связей: несвободное твердое тело можно рассматривать как свободное, если его мысленно освободить от связей,заменив их действие реакциями. В статике этот принцип позволяет рассматривать равновесие несвободного твердого тела как свободного под действием активных (заданных) сил и реакций связей.

    Рассмотрим наиболее часто встречающиеся типы связей на плоскости и направления их реакций.

1. Гладкая плоскость (поверхность) или опора

Р еакция N гладкой плоскости (поверхности) или опоры направлена по общей нормали к поверхностям соприкасающихся тел в точке их касания и приложена к этой точке.

   

2 . Гибкая нить (провода, канаты, цепи, ремни)

Реакция Т направлена вдоль нити к точке подвеса.

   

3 . Невесомый стержень с шарнирами

Реакция N невесомого стержня направлена вдоль стержня. Обычно реакция Nизображается от тела по стержню, в предположении, что в равновесии стержень растянут.

 

   4 . Неподвижный цилиндрический шарнир или подшипник

Реакция R_A цилиндрического шарнира может иметь любое направление в плоскости, перпендикулярной оси вращения, т. е. в плоскости Аху. Обычно ее раскладывают на две составляющие Х_А и Y_A по двум взаимноперпендикулярным направлениям.

5. Шарнирно-подвижная опора (опора на катках)

Р еакция R проходит через ось шарнира и направлена перпендикулярно к опорной плоскости.