Верёвочный многоугольник

Перевод

Верёвочный многоугольник

        графический метод отыскания опорных реакций и равнодействующих системы сил, построения эпюр изгибающих моментов, определения рациональных очертаний арочных и висячих систем и решения др. задач статики плоских систем. В основу построения В. м. положено представление о многоугольнике, образованном осью закрепленной по концам невесомой нити (верёвки), натянутой действующими на неё силами. Построение В. м. совместно с силовым многоугольником (рис.) применяется также для определения геометрических характеристик плоских сечений, решения некоторых задач инженерной гидравлики, экономики и др.

        

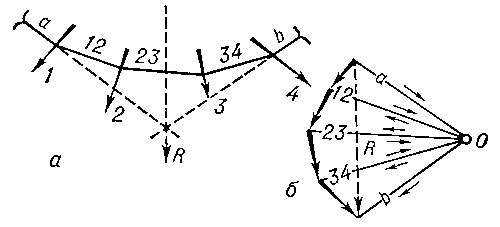
        а — веревочный многоугольник; б — силовой многоугольник.

5.2. Определение усилий в стержнях фермы методом вырезания узлов

 

Рассмотрим определение усилий в стержнях фермы по способу вырезания узлов.

Этот способ состоит в том, что мысленно вырезают узлы фермы, прикладывают к ним соответствующие внешние силы и реакции стержней и составляют уравнения равновесия сил, приложенных к каждому узлу. Так как в начале расчета фермы неизвестно, какие стержни фермы растянуты и какие сжаты, то условно предполагают, что все стержни растянуты (реакции стержней направлены от узлов).

Если в результате вычислений получают ответ со знаком минус, то соответствующий стержень сжат.

Найденные реакции стержней равны по модулю внутренним усилиям в стержнях.

Последовательность рассмотрения узлов определяется обычно условием, что число неизвестных сил, приложенных к узлу, не должно превышать числа уравнений равновесия сил (двух для плоской фермы и трех для пространственной). Тогда эти неизвестные определяются сразу из уравнений равновесия сил, действующих на этот узел.

Усилия в отдельных стержнях загруженной фермы могут оказаться равными нулю. Такие стержни принято называтьнулевыми. Рассмотрим леммы, пользуясь которыми можно определить нулевые стержни плоской фермы, не производя ее расчета.

Лемма 1. Если в незагруженном узле плоской фермы сходятся два стержня, то усилия в этих стержнях равны нулю (рис. 5.4):

 

 

Лемма 2. Если в незагруженном узле плоской фермы сходятся три стержня, из которых два расположены на одной прямой, то усилие в третьем стержне равно нулю. Усилия в первых двух стержнях равны между собой (рис. 5.5):

 

 

Лемма З. Если в узле плоской фермы сходятся два стержня и к узлу приложена внешняя сила, линия действия которой совпадает с осью одного из стержней, то усилие в этом стержне равно по модулю прило­женной силе, а усилие в другом стержне равно нулю (рис. 5.5):

 

 

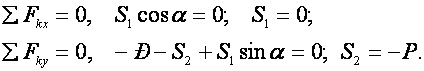
Задача 5.1

Определить способом вырезания узлов усилия в стержнях фермы, изображенной на рис. 5.6, а,  если к узлу F фермы приложена вертикальная сила Р = 120 кН.

Дано: Р = 120 H.

Определить: S₁, S₂, S₃, S₄, S₅, S₆, S₇, S₈, S₉.

 

Решение.

1. Определение опорных реакции фермы

Объект равновесия – ферма. На нее действуют: активная сила   и реакции опор   и  . Определим реакции опор.

 

Так как сила Р = 120 кН, приложенная к узлу фермы F, вертикальна и реакция шарнирно-подвижной опоры В, перпендикулярная опорной плоскости, тоже вертикальна, то линия действия реакции шарнирно-неподвижной опоры Адолжна быть параллельна им, т.е. должна быть тоже вертикальна. Тогда для полученной плоской системы параллельных сил по формулам (3.8) получим:

 

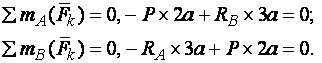                             (а)

 

Решая систему уравнений (а), получим:

 

 

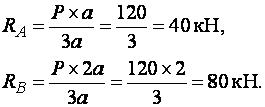
Для того, чтобы убедиться в правильности расчета, вычислим:

 

 

Опорные реакции определены верно.