2.5 Минимизация частичного автомата мили
Попробуем минимизировать количество вершин, в которые и из которых осуществляется переход в таблице. Построим треугольную матрицу:
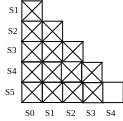
Рис. 2.8
Из треугольной матрицы видно, что S5 эквивалентна S4.
ТПВ минимизированного частичного автомата Мили
Si |
x1x2x3 |
|||||||
000 |
001 |
010 |
011 |
100 |
101 |
110 |
111 |
|
s0 |
s1/0100 |
s1/0100 |
s2/0110 |
s2/0110 |
s3/0001 |
s2/0010 |
s3/0001 |
- |
s1 |
s4/0001 |
s4/0001 |
- |
- |
- |
- |
- |
- |
s2 |
S4/0010 |
s4/0010 |
s2/0010 |
s2/0010 |
- |
S4/0010 |
- |
s2/0010 |
s3 |
s2/0100 |
- |
s2/0100 |
- |
- |
- |
- |
- |
s4 |
s0/1000 |
s0/1000 |
s0/1000 |
s0/1000 |
- |
s0/1000 |
- |
s0/1000 |
Таблица 2.12
Рис. 2.9
Проверка минимизированного частичного автомата Мили
P |
p5 |
p7 |
p5 |
p5, p7 |
p4, p6 |
p0, p2 |
p0 |
p0, p2 |
p3 |
p3 |
p1 |
p1, p3 |
p2 |
S |
s0 |
s2 |
s2 |
s4 |
s0 |
s3 |
s2 |
s4 |
s0 |
s2 |
s2 |
s4 |
s0 |
W |
|
w2 |
w2 |
w2 |
w0 |
w3 |
w1 |
w2 |
w0 |
w4 |
w2 |
w2 |
w0 |
Таблица 2.13
p2 |
p0 |
p0, p2 |
p3 |
p1 |
p1, p3 |
p0 |
p0 |
p0 |
p1 |
p1 |
p1 |
p0 |
|
s2 |
s2 |
s4 |
s0 |
s2 |
s4 |
s0 |
s1 |
s4 |
s0 |
s1 |
s4 |
s0 |
s1 |
w4 |
w2 |
w2 |
w0 |
w4 |
w2 |
w0 |
w1 |
w3 |
w0 |
w1 |
w3 |
w0 |
w1 |
Таблица 2.13 (продолжение)
3 Структурный синтез автомата
3.1 Кодирование состояний автомата
Закодируем состояния автомата способом, минимизирующим число переключений элементов памяти. Для этого составим множество M из пар состояний, между которыми есть переход:
M={(S0,S1),(S0,S2), (S0,S3), (S0,S4), (S2,S3), (S2,S4), (S1,S4)}
Выбираем (S0,S1)
Кодируем соседними кодами
S0=000
S1=001
M={(S0,S2),(S0,S3), (S0,S4), (S2,S3), (S2,S4), (S1,S4)}
Выбираем (S1,S4)
M4={(S1,S4), (S2,S4), (S0,S4)}
B4={S0,S1}
Смотрим множество кодовых расстояний
C4={010, 100}
000
C4={101, 011}
001
Определяем, какой код лучше
d=(010
000)+(010
001)=1+2=3
010
d=(100 000)+(100 001)=1+2=3
100
d=(101 000)+(101 001)=2+1=3
101
d=(011 000)+(011 001)=2+1=3
011
Выбираем любое
S4=011
M={(S0,S2),(S0,S3), (S2,S3), (S2,S4)}
Возьмем (S0,S2)
M2={(S0,S2), (S2,S3), (S2,S4)}
B2={S0,S4}
C2{010, 100}
000
C2{111}
011
d=(010 000)+(010 011)=1+1=2
010
d=(100 000)+(100 011)=1+3=4
100
d=(111 000)+(111 011)=3+1=4
111
Выбираем S2=010, так как d=2
M={(S0,S3), (S2,S3)}
Выбираем (S2,S3)
M3={(S0,S3), (S2,S3)}
B3={S0,S2}
C3{100}
000
C3{110}
010
d=(100 000)+(100 010)=1+2=3
100
d=(110 000)+(110 010)=2+1=3
110
Выбираем любой, пусть
S3=100
Таким образом, получаем следующие коды для состояний:
S |
q1q2q3 |
S0 |
000 |
S1 |
001 |
S2 |
010 |
S3 |
100 |
S4 |
011 |
Таблица 3.1