2.3.2. Расчет прочности сечений.

а) Проверка размеров бетонного сечения ригеля.

Рассмотрим сечение у опоры В, где действует наибольшая поперечная сила.

где b=0,32м, h=0,7 м.

а=0,07м,

Следовательно, принятые размеры достаточны.

б) Расчет продольной арматуры.

В пролете ригель рассматриваем прямоугольного сечения шириной b=0,32 м.

Определяем граничное значение относительной высоты сжатой зоны.

где

В крайнем пролете М=0,70808 кН·м, поэтому

В опорных сечениях ригеля действует отрицательные моменты, поэтому сечение рассматриваем как тавровое.

Определяем положение нулевой линии в тавровом сечении ригеля. Наибольший момент действует у опоры В:

Граница сжатой зоны расположена в полке, поэтому при расчете на действие отрицательных моментов сечения балки рассматриваем как прямоугольное шириной b=b_f^’=0,519 м.

Таблица 13. Армирование ригеля

Сечение балки	As,см2, по расчету	Принятая продольная арматура
		Количество и диаметр, мм, стержней	As,см2
1	19	4⌀25 A400	19,63
В	8,7	2⌀25 A400	9,82
2	19	4⌀25 A400	19,63
С	8,7	2⌀25 A400	9,82

в) Расчет поперечной арматуры

Проверяем необходимость постановки расчетной поперечной арматуры. Так как влияние свесов невелико, в расчетах полагаем и

Наименьшая поперечная сила на приопорных участках действует у опоры А.

Принимая

при (продольные силы отсутствуют), имеем:

Прочность наклонных сечений без поперечной арматуры не обеспечена, поэтому для приопорных участков необходим расчет этой арматуры. Производим расчет для приопорного участка у крайней опоры.

Определяем величину поперечной силы Q_b, воспринимаемой бетоном сжатой зоны в наклонном сечении.

Вычислим длину проекции опасного наклонного сечения:

, то .

Определяем требуемую интенсивность поперечного армирования:

.

Принимаем и определяем шаг хомутов.

Наибольшее допустимое расстояние между хомутами:

По конструктивным требованиям при h>450мм назначаем

Хомуты устанавливаем из арматуры А240.

Из условий сварки минимальный диаметр 8мм.

Требуемая площадь сечения хомутов в одной плоскости

Принимаем 4⌀8 A240 (A_s = 2,01 cм²).

На пролетных участках назначаем шаг хомутов, равный 400 мм. Результаты расчетов приведены в таблице 14.

Таблица 14. Результаты расчета наклонных сечений

Определяемая величина	Ед. изм.		Положение расчетного наклонного сечения у опоры
			А	В слева	В справа	С
Q	кН		96,3	158,6	134,4	123,5
Сb	м		2,1	2,1	2,1	2,1
Qb	кН		109	109	109	109
Сd	м		1,16	0,79	0,94	0,94
Csw	м		1,26
qsw	кН/м		144	230	193	193
smax	м		0,6	0,4	0,5	0,5
ssw	м		0,2	0,1	0,1	0,1
Поперечная арматура	__	4⌀8 A240		4⌀10 A240	4⌀10 A240	4⌀10 A240
Аsw	см2	2,01		3,14	3,14	3,14

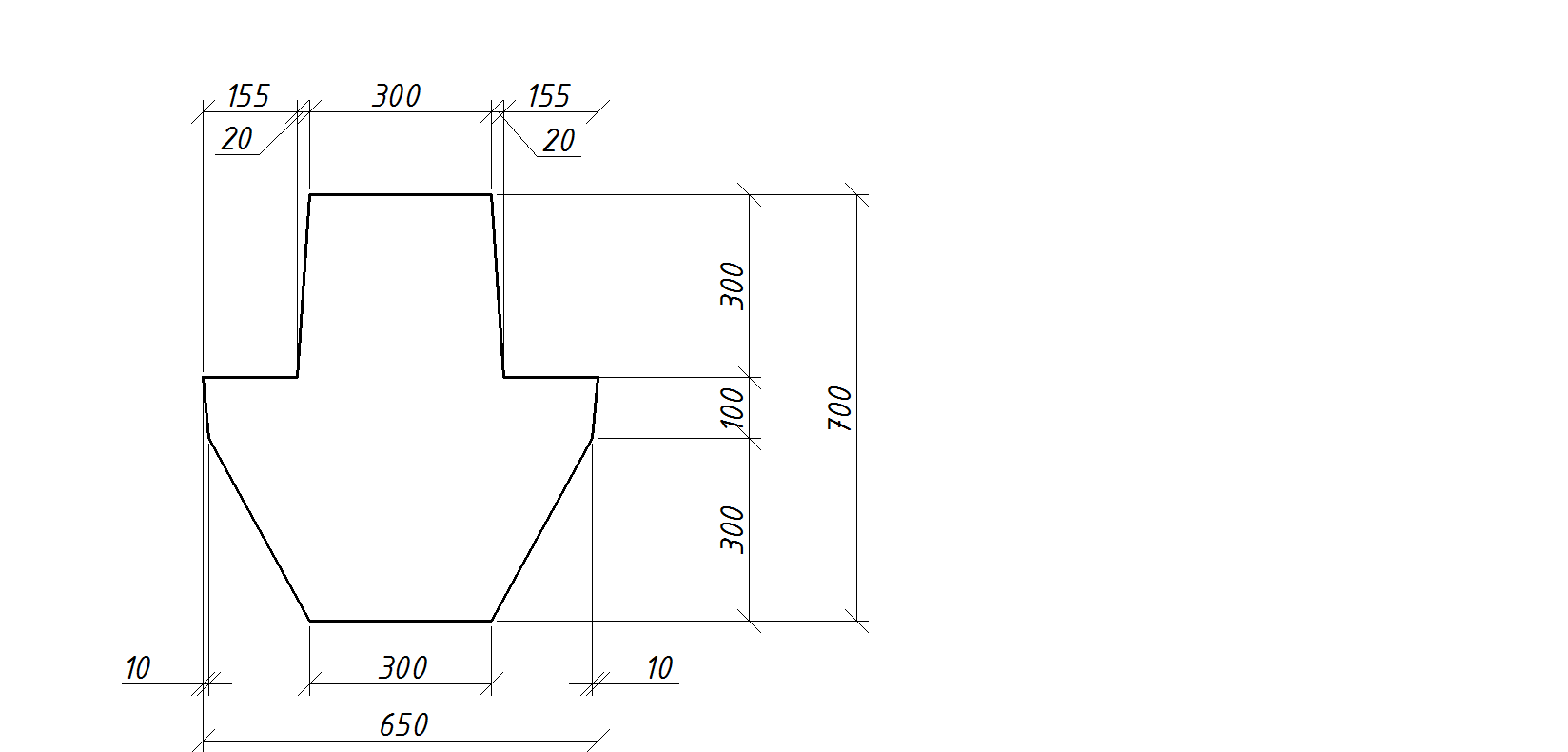
Рисунок 13. Схема ригеля