Таблица 1.

Порядок проектирования балок

Исходные данные: p, q, l, [f / l]
Шаг	Вид стенки
	гибкая	гофрированная	перфорированная
1	Выбор типа сечения, а также
	очертания	типа гофров	типа разреза
2	Выбор марки стали Ryf, Ryw		Ry1, Ry2
3	Выбор высоты былки hopt, hr		hr
4	Выбор гибкости и толщены стенки λw, tw		-
5	Выбор ширины пояса bt		-
6	-	Выбор параметров
		гофра – f, a, a1	отверстия – v, a, n, e
7	Выбор толщины пояса tf min (tf)		-
8	Размещение ребер жесткости и стыков
9	Определение характеристик
	геометрия сечения		исходного двутавра – h0, A0
10	Проверки прочности, устойчивости, жесткости, местной устойчивости
11	Назначение поясных и других швов
12	Расчет ребер жесткости и стыков

4. Расчет балки с гибкой стенкой

К балкам с гибкой стенкой относятся конструкции, которые могут нормально эксплуатироваться после потери местной устой­чивости стенки, если последняя остается упругой.

Долгое время считалось, что эксплуатировать балки с тонкими стенками нельзя, так как потеря местной устойчивости стенки приводит всю балку в предельное состояние. Между тем в само­лето- и судостроении давно обратили внимание на то, что балки с «хлопунами» в тонкой стенке работают достаточно надежно, причем после снятия нагрузки «хлопуны» исчезают.

Уменьшение толщины стенки в 2 ... 3 раза по сравнению с обычными сварными балками и 4 ... 6 раз по сравнению с про­катными снижает долю металла, расходуемого на стенки, с 45...55 до 25...35%. Материал концентрируется в поясах, где эффек­тивность его использования существенно выше. Благодаря этому снижается общая металлоемкость, а следовательно в значитель­ной мере и стоимость балок. Кроме того, повышается хладостойкость стенок, так как при толщине их 2 ... 8 мм (именно такие толщины стенок принимают в балках высотой до 2,5 ... 3 м) трещины в стенках практически не возникают. В безреберных балках с гибкой стенкой, кроме того, уменьшаются трудозатраты на изготовление этих конструкций.

Недостатком балок с гибкой стенкой является то, что образо­вание «хлопунов» иногда сопровождается выстрелоподобным зву­ком. Поэтому надо, чтобы «хлопуны» образовывались уже при постоянных нагрузках и в таком закритическом состоянии балка работала на временные нагрузки. Нежелательно изменение «хло­пунов» при перемене направления действия временных нагрузок. Балки с гибкой стенкой используются при статических нагрузках.

Форма потери устойчивости стенки зависит от вида силовых факторов (М, N, Q), действующих на нее, и их сочетаний (рис. 4.1). В зависимости от вида деформаций (несмотря на различия в на­пряженном состоянии) можно выделить несколько стадий работы отсека (рис. 4.2).

Рисунок 4.1 Формы потери местной устойчивости гибкой стенки

а) при чистом изгибе; б) при чистом сдвиге; в) при центральном сжатии

На первой стадии стенка остается плоской, ее работа не отли­чается от работы балки с обычной стенкой. Протяженность первой стадии невелика (тем короче, чем больше λ_w) и зависит от наличия погибей, возникающих при изготовлении. Оканчивается эта докритическая стадия работы отсека потерей местной устойчивости стенки.

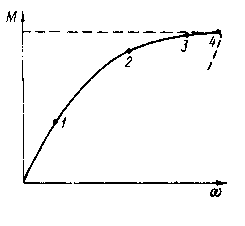
Рисунок 4.2 График боковой деформации гибкой стенки (ω) в зависимости от величины силового фактора (М)

1- стадия работы докритическая; 2 - то же, закритическая упругая; 3- то же, развития пластических деформаций, образование пластического механизма;

4- потеря устойчивости пояса в плоскости балки

Затем наступает стадия закритической упругой работы стенки. Между деформацией стенки и нагрузкой устанавливается нели­нейная зависимость. Появились и развиваются зоны выпучивания стенки, но при снятии нагрузки стенка возвращается в перво­начальное положение. Произошло изменение напряженного со­стояния как в стенке, так и в поясах. Потерявшая устойчивость стенка воздействует на пояса, вызывая в них местный изгиб. Вторая стадия работы завершается в момент достижения напря­жениями величины σ_т либо в отдельных точках стенки или в поя­сах, либо одновременно.

Третья стадия характеризуется развитием пластических де­формаций и в стенке и в поясах. Прогиб балки нарастает. В отсе­ках к концу третьей стадии, по существу, образуется пластиче­ский механизм, при котором балка переходит в предельное состояние и становится не пригодной к эксплуатации из-за появле­ния чрезмерных остаточных де­формаций.

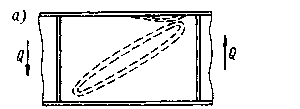
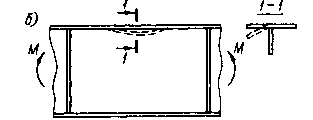
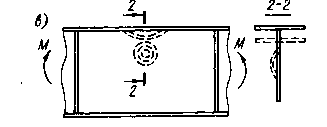
Рисунок 4.3 Характер исчерпания несущей способности моделей балки с гибкой стенкой

а — потеря устойчивости пояса в плоскости балки при сдвиге; б — то же, по кромкам при чистом изгибе; в — то же, в плоскости балки при чистом изгибе.

При дальнейшем даже незна­чительном возрастании нагрузки произойдет либо полная поте­ря несущей способности балки вследствие потери местной устой­чивости полки по кромкам, если толщина ее была выбрана недостаточной, либо потеря устойчи­вости пояса в пределах отсека в плоскости балки от действия сжимающей силы и местного изгибающего момента (рис.4.3).

Балки с гибкой стенкой могут иметь следующие конструк­тивные решения: с поперечными ребрами, двусторонними и одно­сторонними, приваренными к стенке (рис.4.4,б,в); с попереч­ными ребрами, не связанными со стенкой (рис.4.4,г); без попереч­ных ребер (безреберная балка).

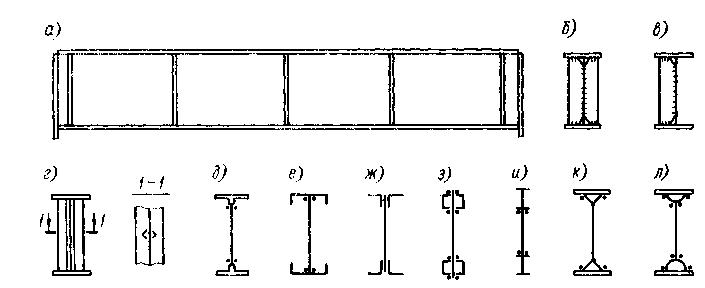
Рисунок 4.4 Балка с гибкой стенкой и поперечными ребрами

а - общий вид балки; б - двусторонние поперечные ребра; в - одностороннее ребро; г - бесконтактные ребра; сечение балки; д - с прокатными таврами; е - с прокатными и гнутыми швеллерами; ж - с уголками; з - с коробчатыми поясами из швел­лера; и - с двутаврами; к — замкнутое с уголками; л - замкнутое с половинками из круглых труб

Поперечные ребра в рассматриваемых конструкциях, как и в обычных балках, устанавливаются для увеличения жесткости в местах опирания второстепенных балок или других элементов, а также с целью ограничения длины отсека. Бесконтактные ребра жесткости, не соединенные со стенкой, также выполняют свое назначение, при этом трудозатраты на изготовление сни­жаются благодаря отсутствию швов на стенке. В безреберных балках уменьшается металлоемкость, а также трудозатраты на изготовление и приварку ребер, однако такие балки требуют строго центрированного приложения нагрузки в их плоскости, ибо пояс у них почти не закреплен от закручивания.

Исследования и опытные разработки показали, что в двутавро­вых балках с гибкой стенкой за счет использования закритической стадии работы при одинаковых марках стали расход металла можно снизить на 10 ... 15%. В балках с более жесткими поясами из тавров, швеллеров и др. экономия металла возрастает до 25%. При таких условиях балки вполне конкурентоспособны с фер­мами, хотя имеют высоту в 1,5 ... 2 раза меньшую.

ПРИМЕР. Определить размеры сечения и других элементов стропильной балки с гибкой стенкой (рис. 4.5) в покрытии производст­венного здания пролетом 24 м. Балка свободно оперта на колонны. Кли­матический район II₄. Расчетная нагрузка - 53кН/м; нормативная нагрузка - 39кН/м (эпюры М и Q представлены на рис.4.6).

Принимается тип сечения в виде сварного двутавра с поясами из листов. Балка с параллельными поясами, постоянного сечения.

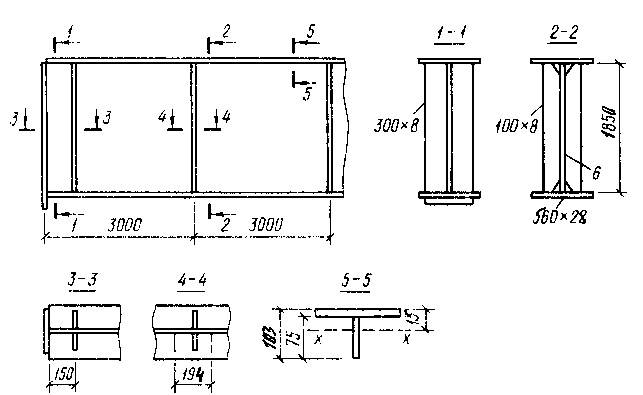
Рисунок 4.5 Размеры балки

Принимается для стенки и поясов одинаковая марка стали С345 (ГОСТ 27772-88), R_yw = 335 МПа для листов толщиной от 2 до 10 мм; R_yf = 300 МПа при тол­щине пояса от 20 до 40 мм. Для ребер жесткости принимаем сталь С245, R_y = 230 МПа.

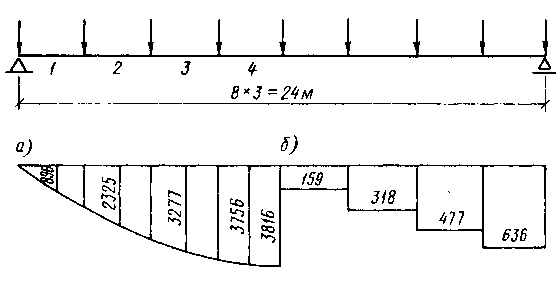
Рисунок 4.6 Схема нагрузки и эпюры усилий

а - изгибающих моментов (кН∙м); б - поперечных сил (кН)

Определяем высоту балки из условия жесткости при [f/l] = 1/250;

h_r =5σ_nf∙ ∙[l/f]∙l/24Е∙α,

где σ_nf=R_yf(qⁿ/q)=300(39/53)=220 МПа – напряжения от общего изгиба в поясе, возникающего от действия заданной нормативной нагрузки;

- для балок с ребрами в пролете;

- для балок без ребер в пролете.

Принимаем , тогда α =1,2-0,033·13 = 0,75 → .

Оптимальная высота балки h_орt = (1/13...1/15)l/1,15=l/(15...17)=1,6...1,4м. Поскольку определяющим является условие жесткости, окончательно принимается h_w = 1850 мм.

По таблице 4.1 выбирается оптимальная гибкость стенки λ_w,opt ≈ 260.

Таблица 4.1

Оптимальные гибкости стенки

l, м	q, кН/м	Гибкости при к
		0,045	0,25
12	10 30 50	380 280 260	300 290 280
24	10 30 50	455 300 260	530 420 370
36	10 30 50	470 355 300	600 490 400

- безразмерный коэффициент, оценивающий относительную жесткость поясных листов: для листов к ≈ 0,03 … 0,045, для поясов из тавров и швеллеров к ≈ 0,25.

С учетом поправки на сталь с R_yw = 335 МПа, гибкость Толщина стенки t_w = 1850/328 = 5,64 мм; ближайшая толщина по сокра­щенному сортаменту 6 мм. Тогда

; .

Ширина пояса из условия обеспечения общей устойчивости при l_ef =3 м находится по формуле: →

ши­рину пояса принимаем b_f = 560 мм (ГОСТ 82-70).

Минимальная толщина пояса из условия местной устойчивости по формуле: ,

По сортаменту принимаем t_f = 28 мм.

Поперечные ребра устанавливаются на рас­стоянии 3 м в местах опирания элементов покрытия. Размеры парного симметричного ребра . Принимаем b_h = 100 мм, толщина ребра (принимаем t_s = 8 мм).

Дополнительное ребро устанавливается на расстоянии 150 мм от опорного, исходя из условия → 100 ≤ b ≤ 190 мм.

Ширину опорного ребра принимаем b_r=300 мм ≤ b_f. Толщина ребра из условия прочности на смятие (принимаем 8 мм).

Далее следует проверить прочность балки во всех четырех отсеках по среднему сечению:

.

М_u – предельное значение момента, вычисляемое по формуле

Q_u – предельное значение поперечной силы, вычисляемое по формуле:

Характеристики условного пояса - тавра (см. рис. 4.5):

высота уча­стка стенки .

h_t = t_f+h_w1 = 2,8+7,5 = 10,3 см;

А_f = b_f∙t_f+h_w1t_w = 56·2,8+7,5·0,6 = 156,8+4,5 = 161,3 см²;

y = (S_f+S_w1)/A = (156,8 · 1,4 + 4,5 · 6,55)/161,3= 1,54 см;

I_f = b_ft_f³/12+t_wh_w1³/12+b_ft_f(y - t_f/2)²+t_wh_w1·(h_w1/2+ t_f - y)²=

= 56·2,8³/12+0,6·7,5³/12+156,8·0,14²+4,5·5,01²=239,6 см⁴;

W_min = I_f /(h_t - y) = 239,6/8,76 = 27,4 см³;

=8·27,4·(185² + 285²)/(0,6·185²·285²) = 0,0152;

a – шаг ребер жесткости, для первого отсека а = 285 см;

при α ≤ 0,03 → β = 0,05 + 5α ≥ 0,15

при 0,03 ≤ α ≤ 0,1 → β = 0,11 + 3α ≤ 0,40

β = 0,05 + 5·0,0152 = 0,126 (принимается β= 0,15).