Министерство общего и профессионального образования

Российской Федерации

НИЖЕГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Им. Р.Е.АЛЕКСЕЕВА

А.А. ШТЕРНОВ

РАСЧЕТ ЭЛЕМЕНТАРНОЙ БАЗЫ

МИКРОЭЛЕКТРОНИКИ

СБОРНИК ЗАДАЧ

Нижний Новгород

1997г.

ББК 32.884.1

Ш 904

УДК 621.396.6+621.382

Расчет элементарной базы микроэлектроники: Сборник задач/ А.А. Штернов; Нижнегород. Гос. Тех.ун-т. Н. Новгород, 1997.

Содержит задачи и контрольные вопромы, комментарии к ним. Приводятся решения нескольких задач.

Предназначен для студентов специальностей «Конструирование и технология производства радиоэлектронных средств», «Телекоммуникации», «Технология материалов и изделий электронной техники» всех форм обучения.

Рис. 18. Табл. 3. Библиогр.: 4 назв.

Рецензенты: канд. физ.-мат. наук В.Д. Скупов, канд. техн. наук А.М. Шутов

Штернов А.А. 1997

ОГЛАВЛЕНИЕ

Предисловие

1. Физика полупроводников

2. Полупроводниковые диоды

3. Биполярные транзисторы

4. Полевые структуры

5. Расчет диффузионных процессов. Окисление.

6. Чистые материалы. Получение структур методом сплавления

Приложение1

Приложение2

Важнейшие электрофизические характеристики металлов

Библиографический список

Предисловие

Путь к пониманию истины зачастую ведет через барьеры -порой достаточно крутые и сложные.

Б.Шкловский

Одним из примеров таких барьеров, хотя и не очень крутых да и не всегда сложных, являются приведенные ниже задачи и контрольные вопросы по основным разделам лекционного курса "Физические основы микроэлектроники ", составленные с целью их использования как в ходе практических занятий, так и для самопроверки усвоения знаний.

Решение задач параллельно с изучением материала по источникам информации способствует приобретению требуемых знаний при оптимальном расходе энергии и времени студентов.

Задачи сгруппированы по темам: физика полупроводников, полупроводниковые диоды, биполярные транзисторы, волевые структуры. диффузионные и окислительные процессы, получение структур методом сплавления и чистые материалы.

Большинство задач дает возможность студентам применить на практике сформулированные в лекционном курсе идеи и выведенные соотношения. Среди них имеются сравнительно простые задачи и контрольные вопросы, которые решаются непосредственным использованием полученных в лекционном курсе формул; для решения ряда других задач необходимо самостоятельно проделать выкладки, о которых в лекциях лишь упоминалось. В любом случае в результате работы с задачами студенты получают ясное представление о порядке различных практически важных величин. Приведенные задачи полезны еще и тем, что привлекают внимание к определенным операциям или процедурам, представляющим особый интерес.

Для некоторых (более сложных) задач приводится решение; в отдельных случаях, имеющих практически важное значение, решение снабжено краткими комментариями.

Задачи могут быть использованы для возможной сдачи данного предмета по разделам в процессе обучения в течение семестра. В этом случае каждая задача оценивается в баллах и при получении студентом заданного преподавателем количества баллов раздел может быть зачтен с оценкой (в зависимости от суммы набранных баллов). В процессе изучения дисциплины студенты заранее подбирают вопросы и задачи, обеспечивающие получение нужного количества баллов, и после освоения раздела курса сдают их преподавателю в часы консультаций в форме собеседования по выбранным вопросам.

Соотношений по каждому разделу, таблицы некоторых функций и характеристики важнейших полупроводниковых материалов.

Приведенные задачи могут быть использованы также при изучении дисциплин "Электронное материаловедение", "Твердотельные электронные приборы", "Технология материалов и изделий электронной техники".

Постоянное внимание к работе, регулярный обмен мнениями и большая помощь со стороны коллег по кафедре "Конструирование и технология производства радиоаппаратуры", особенно Ю.Я, Короткова, И.Н Мерзлякова, С.М. Никулина, М.В, Ширяева, В значительной степени способствовали улучшению настоящего пособия, и автор приносит им искреннюю благодарность.

Дорогу осилит идущий!

1. Физика полупроводников

Полупроводник – материал одним из основных свойств которого является отрицательное значение температурного коэффициента сопротивления.

Докажите, что это именно так, и поясните почему. Но всегда ли это справедливо? Для любых ли температурных интервалов?

1. Для беспримесного кремния найдите расстояние от уровня Ферми до середины запрещенной зоны при условии, что эффективная масса электрон в зоне проводимости в двое меньше эффективной массы дырки в валентной зоне.

2. Будут ли какие –либо из плоскостей {111} нормальны к каким-нибудь плоскостям 011}? Если да, приведите пример.

3. Нарисуйте плоскости (001),(110), (111) в кубическом кристалле.

4. Подсчитайте минимальное расстояние между плоскостями {120} в кремнии, если длина ребра элементарной ячейки равна 0,543 нм.

5. Определите индексы Миллера и направление отмеченных плоскостей (рис. 1).

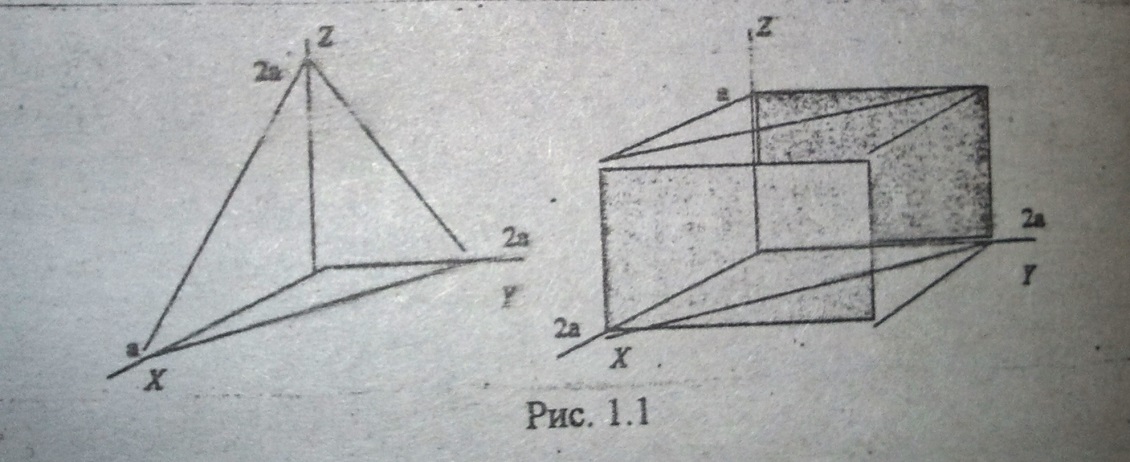
6. Плоскость пересекает оси кубического кристалла в точках За, 2а, 2а, где а - длина ребра элементарной ячейки, Найдите индексы Миллера и направление этой плоскости.

7. Определите вероятность заполнения уровня, лежащего на 0,863 эВ выше уровня Ферми в беспримесном кремнии при Т=1000 К.

8. Посчитайте число электронов в единице объема в зоне проводимости беспримесного кремния про Т=300К.

9. Плотность состояний задается формулой N(E) = CE^0.5. где C = [(2m₀4π²/h²)^1.5]/2π², m₀ –масса электрона. Выразите через С уровень Ферми при Т=0.

10. Ширина запрещенной зоны кремния 1,12 эВ, Найдите концентрацию пятивалентной примеси. необходимую для сдвига уровня Ферми на границу зоны проводимости при Т= 300 К.

11. В образец чистого кремния введены атомы фосфора с концентрацией 10¹⁶ см^-3, атомы примеси распределены равномерно. Найдите удельное сопротивление образца при Т = 300 К. Какое будет результирующее удельное сопротивление и тип проводимости образца, если в добавление к фосфору внести 10¹⁷ см^-3 атомов бора, распределенных равномерно? Изобразите диаграмму энергетических зон для последнего случая и покажите положение уровня Ферми, Если оно изменилось, то объясните почему.

12. Ширина запрещенной зоны зоны Е_g собственного кремния равна 1,12 эВ. Найдите вероятность заполнения электроном уровня вблизи дна зоны проводимости при температурах от 0 до 300 К. Как изменится эта вероятность при указанных температурах, если на полупроводник будет действовать электромагнитное излучение с длинами волн 0,6 и 2,0 мкм? Считать, что при Т=300к Е_с-Е_F ≈ E_g/2.

Решение:

1. Функция распределения Ферми-Дирака имеет вид f(E,T)=[+exp(E-E_f)/kT]^-1, где f(E,T) – вероятность того, что электрон имеет энергию Е. При Е=0 E>E_f, exp(E-E_f)/kT→∞ и f(E,T)→0. Следовательно, энергия электрона не превышает E_f .

Вероятность того, что при температуре Т=300К электрон обладает энергией Е относительно дна зоны проводимости, равна:

f(E,300)=[1+exp(0,56*1,6-10^-19/11,38-10^-23*300)]^-1=(1+е^21,6)^-1≈4*10^-10.

2. Если на полупроводник действует излучение с длиной волны λ=0,6 мкм, то частота этого излучения ν=с/λ=5*10¹⁴ Гц, а энергия Е=hν=2.14эВ (h- постоянная Планка). Поскольку в данном случае энергия излучения (2,1 эВ) больше ширины запрещенной зоны (1,12 эВ), то вероятность нахождения электронов в зоне проводимости увеличивается как при Т=0, так и при Т=300 К.

Если же на полупроводник действует излучение с длиной волны λ=2 мкм, то Е ≈ 0,62 эВ и никакого изменения вероятности не происходит ни при Т=0, ни при Т=300К.

13. Движение пятого электрона на внешней орбите примесного атома V группы в полупроводнике 1 V группы можно приближенно рассматривать как, круговое по орбите вокруг единичного положительного заряда через вещество диэлектрической проницаемостью основного материала. Покажите что электрону требуется энергия около 0,1 эВ для того, чтобы освободиться и стать электроном проводимости в кристалле с относительной диэлектрической проницаемостью ε =12. Определите радиус орбиты основного состояния и тем самым подтвердите предположение, что электрон движется в среде с диэлектрической проницаемостью основного материала. Постоянная решетки а=5,42*10^-4 мкм.

Решение:

Энергия связи Е_n=-13.6Z²/(ε²n²)/ Для Z=1, n=1, ε=12 имеем Е_n=0,094 эВ.

Радиус орбиты r=ε₀εh²n² /πmq²Z = 6.35*10^-4 мкм, это свидетельствует о том, что наименьшая орбита проходит за пределами ближайшего соседнего атома, т.е. в среде основного материала.

14. Найдите положение уровня Ферми в собственном полупроводнике относительно середины запрещенной зоны при комнатной температуре (Т = 300 К), если эффективная масса электрона меньше эффективной массы дырки.

15. В каких случаях примесные атомы дают отдельные уровни, а в каких образуют примесную зону? Когда можно считать, распределение электронов по энергиям экспоненциальным и почему?

16. Поясните, что такое основные и неосновные носители заряда. Как связаны между собой их равновесные концентрации? В каких полупроводниках концентрация неосновных носителей больше : в слаболегированных или в сильнолегированных?

17. Что такое собственная электропроводность? Может ли примесный полупроводник обладать собственной электропроводностью? При каком приращении температуры электропроводность собственного кремния увеличится вдвое по сравнению с его электропроводностью при комнатной температуре?

18. Определите удельное сопротивление собственного германия при комнатной температуре. Как оно изменится, если к этому образцу добавить донорную примесь так, чтобы на каждые 10⁸ атомов германия приходился один атом примеси?

19. Брусок кремния размером 10х10х10 мм при Т = 300 К содержит в качестве примесей галлий с концентрацией N_A = 1,5·10¹⁹ атом/м³ и мышьяк с концентрацией N_Д = 1,5*10¹⁹ атом/м³, Определите сопротивление бруска между двумя противоположными гранями, если концентрация собственных носителей заряда n_i = 1,5·10¹⁶ м^-3, подвижность электронов μ_n =0.12 м² /(В*с), подвижность дырок μ_р =0,05 м² /(В*с).

20. Пластина кремния легирована донорной примесью с концентрацией N_Д=10¹⁵ см^-3. Найдите: а) концентрации электронов и дырок и положение уровня Ферми относительно собственного уровня Ферми; б) результирующие концентрации носителей заряда и положение уровня Ферми, если свет, падающий на пластину, приводит к возникновению фотогенерированных электронов и дырок со стационарной концентрацией 10¹² см^-3). Толщина пластины мала по сравнению с глубиной проникновения света; в) повторите расчеты пункта "б" в предположении, что интенсивность света возросла настолько, что генерируется 10¹⁸ см^-3 электронно-дырочных пар.

21. В кремниевом кристалле электрическое поле в плоскости х_i (перпендикулярной оси х) не равно нулю. При х= х_i концентрация электронов равна 10⁶ см^-3. В направлении, перпендикулярном этой плоскости (вдоль оси х_i), распределение электронов неравномерно. Известно, что ток электронов через плоскость х_i равен нулю. Объясните, почему не течет ток. Чему равен градиент концентрации электронов в направлении, перпендикулярном плоскости х, если напряжённость электрического поля ξ =-10³ В/см (т.е. поле действует в отрицательном направлении относительно оси х).

22. Рассчитайте показатель качества М_Н холловского элемента, определяемый как напряжение Холла, приходящееся на единицу магнитного поля и единицу рассеиваемой мощности. Рассмотрите элемент р-типа, имеющий R_H = 8*10³ см³ /Кл, W/L=1, r=1,2, t= 8мкм (рис.1.2). Вычислите сопротивление такого элемента и значение М_Н, если В=500 Гс, а мощность рассеиваемая элементом, равно 1,43 мВт (считать что μ_р =475 см² /(В*с)).

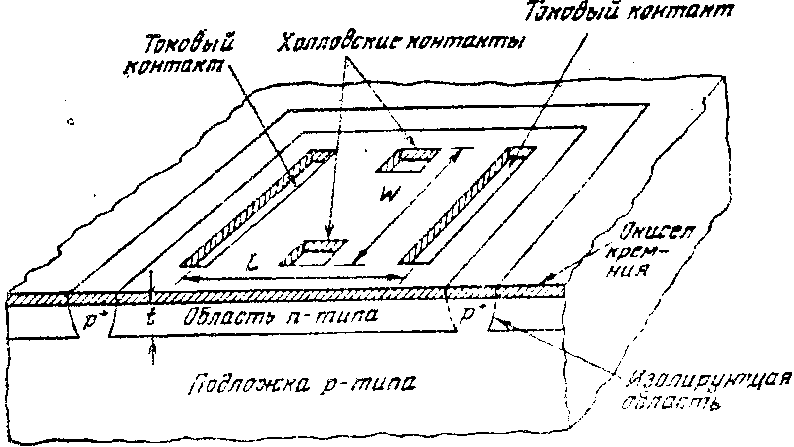
Рис.1.2

Решение:

Одно из важнейших соображений, которое учитывается при проектировании холловского элемента, связано с мощностью, рассеиваемой прибором. Чтобы рассмотреть потребление мощности целесообразно выразить сопротивление холловского элемента через коэффициент Холла. Например, для элемента с проводимостью р-типа и площадью А

R=ρL/A = L/(q μ_р pWt)=L(R_H /r μ_рWt).

Поэтому, если напряжение питания равно U_s то можно записать I= rU_sμ_рWt/R_HL_. Тогда напряжение Холла V_H = rU_sμ_р (W/L)B*10^-8, где В измеряется в градусах, а длинна в сантиметрах.

Из полученного результата следует, что М_Н можно улучшить, снижая напряжение питания и уменьшая концентрацию легирующих примесей и толщину элемента.

Вычисляя параметры, получим: р=r/qR_H) = 9,38*10¹⁴ см ^-3,

R=17,5 кОм. Поскольку Р_Н = U_s²/R, то U_s =(Р_Н*R)^0,5 =5B. Таким образом, М_Н =0,02.

23. В собственном германиевом полупроводнике при 300 К подвижность электронов μ_n = 3900 см² /(В*с), подвижность дырок μ_р= 1900 см² /(В*с). Найдите концентрацию носителей заряда, если измеренная удельная проводимость образца равна σ=0,01 См/см.

24. Найдите напряженность электрического поля, при которой эффективная подвижность электронов уменьшится в двое по сравнению со значением для слабых полей(Т=300 К).

25. Найдите равновесную концентрацию электронов и дырок, ка так же положение уровня Ферми в кремнии при Т=300 К, если кремний содержит N_As=8*10¹⁶ см^-3 атомов мышьяка As и N_B=2*10¹⁶ см ^-3 атомов бора.

26. Почему подвижность носителей заряда и время их жизни зависят от температуры, концентрации примесей и напряженности электрического поля?

27. Имеется однородная пластина кремния n- типа с концентрацией N_Д=2,25*10¹⁵ см ^-3 при температуре Т = 300К. Первоначально пластинка находилась в равновесном состоянии, затем освещается потоком монохроматического света, после чего возвращается в равновесное состояние. Определите равновесные концентрации n_n0, p_n0,неравновесные концентрации n_n, p_n для значений концентраций избыточных носителей: а) Δn =Δp =10¹³ см^-3 , б) Δn =Δp =10¹⁷ см^-3.Какой уровень инжекции реализуется в каждом случае? Найдите время жизни носителей заряда, если скорость рекомбинации S=10¹⁸ см^-3 *с^-1 .

28. Какова скорость рекомбинации в состоянии термодинамического равновесия?

29. В эксперименте по исследованию эффекта Холла на кремниевом образце 1,0х0,2х0,1 см получены следующие данные: I= 5 мА, B=1 Тл, U=0,245 В (в направлении тока I), U_H=2,0 мВ. Считая, что коэффициент Холла r_H=1,18, определите: а) тип проводимости полупроводника; б) концентрацию основных носителей в нем; в) холловскую подвижность носителей; г) дрейфовую подвижность; д) скорость диффузии.

30. Имеется образец невырожденного, равномерно легированного проводника, n-типа, размеры которого таковы, что можно пренебречь влиянием поверхности. При х=0 существует однородный источник, создающий избыточную концентрацию неосновных носителей, изменяющуюся лишь в направлении оси х. внешнее электрическое поле отсутствует, и система находится в стационарном состоянии. Найдите: а) концентрацию неосновных носителей как функцию переменной х; б) плотность диффузионных токов неосновных и основных носителей в предположении, что D_n = 2D_p ; в) плотность дрейфового тока основных носителей; г) напряженность электрического поля в образке.

31. Имеется полупроводник р-типа. Каким будет положение уровня Ферми относительно энергии акцепторного уровня при Т=0 и при Т>0?

32. Образец кремния находится в состоянии термодинамического равновесия и содержит донорные примеси с концентрацией N_Д = 10¹⁶ см^-3 . Найдите температуру, при которой р = 0,1n.

33. Образец германия находится в равновесном состоянии при Т= 400 К. Определите: а) концентрацию дырок и электронов, если образец легирован атомами сурьмы (элемент V группы ) с концентрацией 2,4*10¹³ см^-3 ; б) концентрацию носителей, которая установится после того как образец будет дополнительно легирован атомами индия (элемент 111 группы) с концентрацией 4,8*10¹³ см^-3 .

34. Поясните, будет ли компенсированный материал иметь то же удельное сопротивление, что и собственный полупроводник.

35. Покажите, что в слаболегированном полупроводнике у дельное сопротивление максимально при условии μ_n/μ_р > 1. Вычислите концентрацию акцепторной примеси для кремния, которая потребуется для достижения максимального удельного сопротивления(μ_n ^Si/μ_р^Si =2,18; n_i=1,4*10¹⁰ см^-3).

36. Пластина германия n-типа с удельным сопротивлением 0,1 Ом*см имеет ширину 10^-2 см. К пластине приложена разность потенциалов 1 В. Определите: а) плотность тока; б) время, необходимое для того, чтобы носитель заряда пересек пластину; в) отношение плотностей токов дырок и электронов(μ_n=3900 см^-2/(B*c); μ_р=1900 см^-2/(B*c); n_i=2,4*10¹³ см^-3).

37. Имеется образец германия с поперечным сечением 0,1х0,2 см и концентрацией примеси 10¹⁷ см^-3 . Вдоль образца протекает ток 0,6 А. Перпендикулярно направлению тока действует магнитное поле с индукцией 0,5 Тл. Определите напряжение Холла между контактами к узким сторонам боковой поверхности образца.

38. Кристалл кремния, содержащий в качестве примеси 10^-4 % ат. мышьяка, сначала равномерно легируется 3*10¹⁶ атом/см³ фосфором и после этого также равномерно 10¹⁸ атом/см³ бором. Термический отжиг полностью активизирует все примеси. Какой тип проводимости буш-т иметь кристалл и чему будет равна концентрация основных носителей?

Решение:

Мышьяк – донор. Так как кремний содержит 5*10²² атом/см³ , то концентрация примеси равна 10-4 % ат., означает, что степень легирования кремния равна 2*10²²*10^-6 =5*10¹⁶ атом/см³ . Дополнительное легирование фосфором увеличивает содержание доноров в кристалле до 8*10¹⁶ атом/см³ . Последующее легирование бором изменят тип проводимости. Но вследствие компенсации концентрация акцепторов будет меньше концентрации атомов бора. Из уравнения электронейтральности получим:

р=N_А(B)-[N_Д(As)+ N_Д(P)]=10¹⁸ - (5*10¹⁶ +3*10¹⁶)=9,2*10¹⁷ см^-3).

39. Найдите равновесную концентрацию электронов и дырок, а так же положение уровня Ферми (по отношению к середине запрещенной зоны) в кремнии при Т=300К, если он содержит 8*10¹⁶ см^-3 атомов мышьяка As и 2*10¹⁶ см^-3 атомов бора В.

Решение:

Поскольку концентрация доноров превышает концентрацию акцепторов, кристалл кремния имеет электропроводность n- типа. Результирующая концентрация легирующих примесей равна разности концентраций доноров и акцепторов: N_эфф =N_Д – N_А =6*10¹⁶ см^-3.

Концентрация электронов (основные носители) равна результирующей концентрации легирующей примеси n=6*1016 см-3, концентрация дырок может быть найдена из закона действующих масс p=n_i² /n=3,5*10³ см^-3.

Положение уровня Ферми относительно середины запрещенной зоны найдем из соотношения E_F –E_i =kT ln(n/n_i) = 0,0258 ln(6*10¹⁶ /1,45*10¹⁰)= 0,393 эВ.

Следует отметить, что положение уровня Ферми относительно дна зоны проводимости может быть определено из уравнения E_C-E_F =0,0258 ln(2,8*10¹⁹ /6*10¹⁰)= 0,159 эВ.

Сумма этих двух энергий равна 0,55 эВ, т.е. половине ширины запрещенной зоны кремния.

Нарисуйте зонную диаграмму, отражающую результаты решения этой задачи.

40. Перечислите наиболее характерные признаки и свойства полупроводников.