5. Аналитическое определение аналогов скоростей и ускорений в Mathcad.
Продифференцируем уравнения геометрического анализа по времени, в результате получим уравнения содержащие аналоги скоростей. При повторном дифференцировании получим уравнения содержащие аналоги ускорений
Прототип 1
Прототип 2
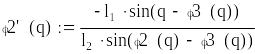
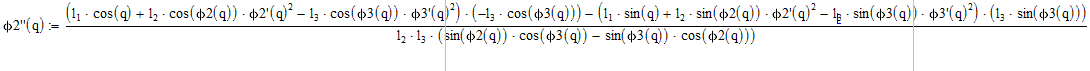
Кинематический анализ механизма. Задачи кинематического анализа.
Задачей кинематического анализа является определение скоростей и ускорений точек механизма, угловых скоростей и ускорений его звеньев при заданных законах изменения обобщенных скоростей q˙s(t) и обобщенных ускорений q¨s(t), то есть первых и вторых производных по времени от обобщенных входных координат.
При заданных q˙s(t) задача определения скоростей и угловых скоростей сводится к определению первых частных производных от функций положения по обобщенным координатам. Эти производные называются первыми геометрическими передаточными функциями механизма или аналогами скоростей.
При заданных q˙s(t) и q¨s(t) определение ускорений сводится к определению кроме первых, еще и вторых частных производных от функций положения по обобщенным координатам; их называют вторыми геометрическими передаточными функциями механизма или аналогами ускорения.
Аналитическое исследование кинематики механизма.
Прототип 1.
xa=l1·cos q
ya=l1·sin q
xa’=-l1·sin q
ya’=l1·cos q
xa’’=-l1·cos q
ya’’=l1·sin q
XA+ l2·cos2 = XO2 + l3·cos3
YA + l2·sin2 = YO2 + l3·sin3
xa’-l2·sin2·2’=-l3·sin3·3’
ya’+l2·cos2·2’=l3·cos3·3’
xa’’-l2·cos2 ·(2’)2-l2·sin2·2’’ = -l3·cos3·( 3’)2-l3·sin3 ·3’’
ya’’-l2·sin2·(2’)2+l2·cos2 ·2’’ = -l3·sin3·( 3’)2+l3·cos3·3’’
xc=xo2+CO2·cos(3+)
ya=yo2+CO2·sin(3+)
0 = -l3·sin3·3’ - l4·sin4·4’
yc’=l3·cos3·3’+ l4·cos4·4’
0 = l3·cos3·(3’)2+l3·sin3·3’’ +l3·cos4·(4’)2+l3·sin4·4’’
yc’’=l3·sin3·(3’)2-l3·cos3·3’’+ l4·sin4·(4’)2-l4·cos4·4’’
Прототип 2:
xa=l1 cos q1
ya=l1 sin q1
xa’=-l1 sin q1
ya’=l1 cos q1
xa’’=-l1 cos q1
ya’’=l1 sin q1
xa+l2·cos=xo2+l3·cos3
ya+l2·sin2=yo2+l3·sin3
xa’-l2·sin2·2’=-l3·sin3·3’
ya’+l2·cos2·2’=l3·cos3·3’
xa’’-l2·cos2 ·(2’)2-l2·sin2·2’’=-l3·cos3·( 3’)2-l3·sin3 ·3’’
ya’’-l2·sin2·(2’)2+l2·cos2 ·2’’=-l3·sin3·( 3’)2+l3·cos3·3’’
xE=xO2+CO2·cos3+l4·cos4
yE=yO2+CO2·sin3 +l4·sin4
xE’=-CO2·sin3·3’-l4·sin4·4’
yE’=CO2·cos3·3’+ l4·cos4·4’
xE’’=CO2·cos3·(3’)2+CO2·sin3·3’’-l4·cos4·(4’)2-l4·sin4·4’’
yE’’=CO2·sin3·(3’)2-CO2·cos3·3’’-l4·sin4·(4’)2+l4·cos4·4’’