II. Статистический анализ экспериментальных данных

1) Результаты ресурсных «испытаний», полученные на первом этапе сводим в расчетную таблицу для нахождения функции распределения наработки. По накопленному числу отказов рассчитаем накопленную частоту и построим график статистической функции распределения наработки :

Рисунок 7

2) Вероятность безотказной работы по определению есть

.

Строим график статистической вероятности безотказной работы: :

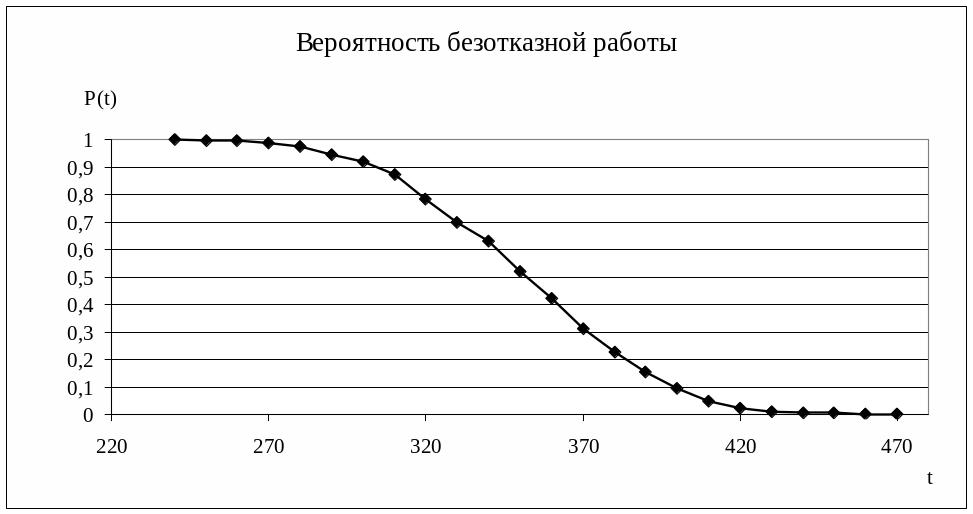
Рисунок 8

3) Гистограммой относительных частот называют сту­пенчатую фигуру, состоящую из прямоугольников, осно­ваниями которых служат частичные интервалы (в нашем случае ширина интервала равна шагу времени наблюдений =10 час), а высоты равны отношению (плотность относительной частоты). Строим гистограмму наработки :

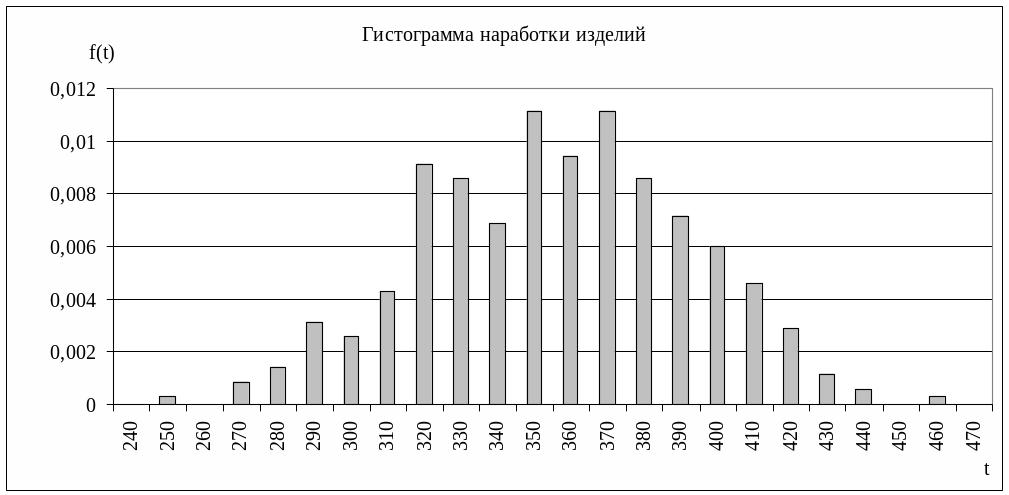
Рисунок 9

Таблица 3 Расчетная таблица

Номер	Время наблюдения	Кол-во исправных изделий	Число отказов	Накопленное число отказов	Частота отказов	Накопленная частота отказов		Среднее число исправных изделий	Интенсивность отказов	Теоретические вероятности
	час
1	240	350	0	0	0	0	0	350	0	7,23E-05	0,00077	7,23E-05
2	250	349	1	1	0,002857	0,002857	0,000286	349,5	0,002861	0,000165	0,001901	8,79E-05
3	260	349	0	1	0	0,002857	0	349	0	0,000351	0,00438	0,000351
4	270	346	3	4	0,008571	0,011429	0,000857	347,5	0,008633	0,00069	0,009425	4,03E-05
5	280	341	5	9	0,014286	0,025714	0,001429	343,5	0,014556	0,001262	0,018962	2,19E-05
6	290	330	11	20	0,031429	0,057143	0,003143	335,5	0,032787	0,002143	0,035704	0,000467
7	300	321	9	29	0,025714	0,082857	0,002571	325,5	0,02765	0,003376	0,063001	0,000192
8	310	306	15	44	0,042857	0,125714	0,004286	313,5	0,047847	0,004938	0,10433	8,61E-05
9	320	274	32	76	0,091429	0,217143	0,009143	290	0,110345	0,006704	0,162447	0,000887
10	330	244	30	106	0,085714	0,302857	0,008571	259	0,11583	0,008449	0,238343	1,78E-06
11	340	220	24	130	0,068571	0,371429	0,006857	232	0,103448	0,009884	0,33039	0,000927
12	350	181	39	169	0,111429	0,482857	0,011143	200,5	0,194514	0,010734	0,434067	1,55E-05
13	360	148	33	202	0,094286	0,577143	0,009429	164,5	0,200608	0,010822	0,542517	0,000179
14	370	109	39	241	0,111429	0,688571	0,011143	128,5	0,303502	0,010127	0,647873	0,000102
15	380	79	30	271	0,085714	0,774286	0,008571	94	0,319149	0,008797	0,742925	5,79E-06
16	390	54	25	296	0,071429	0,845714	0,007143	66,5	0,37594	0,007094	0,822568	3,37E-07
17	400	33	21	317	0,06	0,905714	0,006	43,5	0,482759	0,00531	0,884542	8,96E-05
18	410	17	16	333	0,045714	0,951429	0,004571	25	0,64	0,00369	0,929329	0,000211
19	420	7	10	343	0,028571	0,98	0,002857	12	0,833333	0,00238	0,959387	9,56E-05
20	430	3	4	347	0,011429	0,991429	0,001143	5	0,8	0,001425	0,978122	5,59E-05
21	440	1	2	349	0,005714	0,997143	0,000571	2	1	0,000792	0,988967	6,15E-05
22	450	1	0	349	0	0,997143	0	1	0	0,000409	0,994797	0,000409
23	460	0	1	350	0,002857	1	0,000286	0,5	2	0,000196	0,997708	4,13E-05
24	470	0	0	350		1	0	0	0	8,7E-05	0,999057	8,7E-05
Σ			350		1							0,0045

4) Интенсивность отказа это условная плотность вероятности возникновения отказа, определенная при условии, что до этого момента отказ не возник. Для определения используется следующая статистическая оценка: , где - число отказавших изделий в интервал времени t, - среднее число исправных изделий в интервал времени t: . Строим статистический график интенсивности отказов :

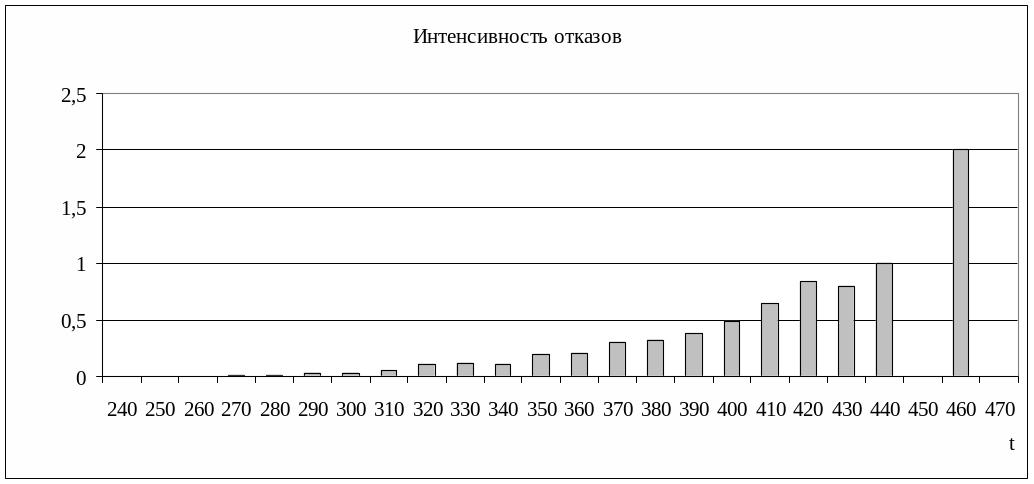
Рисунок 10

Аппроксимируем статистический график интенсивности отказов экспонентой вида . Для этого применим метод наименьших квадратов. Логарифмируя, запишем: . Будем искать параметры и , минимизирующие сумму квадратов отклонений . Это приведет нас к системе уравнений ( - число позиций суммирования)

Таблица 4

250	62500	0,00286123	-5,856503562	-1464,12589	0,007653421
270	72900	0,008633094	-4,752152376	-1283,081142	0,013359933
280	78400	0,014556041	-4,229749199	-1184,329776	0,017651379
290	84100	0,032786885	-3,417726684	-991,1407382	0,023321312
300	90000	0,02764977	-3,588137884	-1076,441365	0,030812528
310	96100	0,04784689	-3,039749159	-942,3222393	0,040710054
320	102400	0,110344828	-2,20414502	-705,3264065	0,05378684
330	108900	0,115830116	-2,15563068	-711,3581244	0,071064119
340	115600	0,103448276	-2,268683541	-771,352404	0,093891164
350	122500	0,194513716	-1,637252601	-573,0384102	0,124050658
360	129600	0,200607903	-1,606403009	-578,3050831	0,163897911
370	136900	0,303501946	-1,192367258	-441,1758855	0,216544804
380	144400	0,319148936	-1,142097401	-433,9970122	0,286102804
390	152100	0,37593985	-0,978326123	-381,5471879	0,378004058
400	160000	0,482758621	-0,7282385	-291,2954001	0,499425612
410	168100	0,64	-0,446287103	-182,9777121	0,659849904
420	176400	0,833333333	-0,182321557	-76,57505385	0,871805302
430	184900	0,8	-0,223143551	-95,95172707	1,151844502
440	193600	1	0	0	1,521837219
460	211600	2	0,693147181	318,8477031	2,656543287
Суммы
7100	2591000		-38,95576803	-11865,49385

Система уравнений принимает вид .

Решением системы является пара коэффициентов: -11,84 и 0,0279. Качество аппроксимации иллюстрирует следующий график

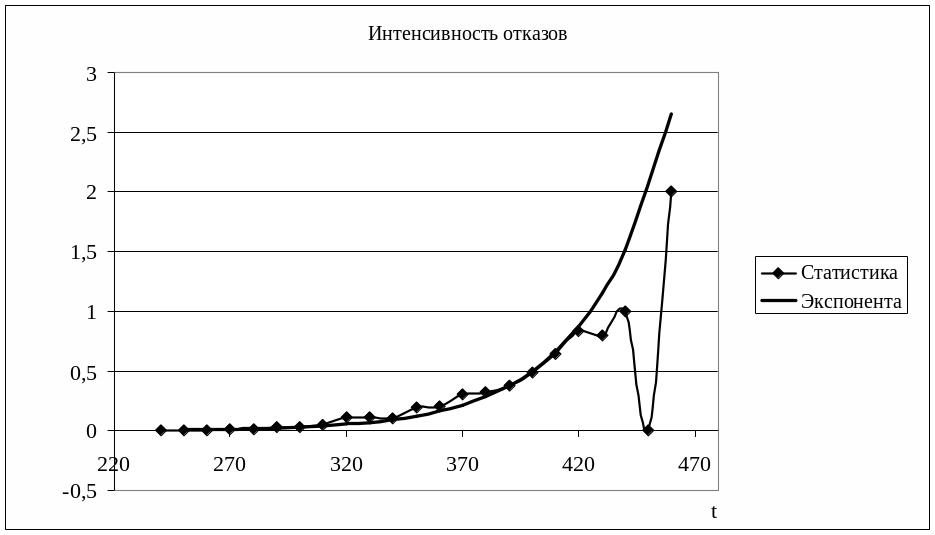
Рисунок 11

Функцию можно представить в виде . Тогда . Отсюда видно, что показатели надежности изучаемых изделий имеют «стареющий» характер. Новые изделия характеризует интенсивность отказов 1/час. В дальнейшем, каждые 100 часов наработки влекут увеличение интенсивности отказов примерно в 16 раз. Или так: рост интенсивности отказов в 10 раз происходит каждые 82,7 часов наработки ресурса.

На практике прибегают к упрощенной, интегральной оценке интенсивности отказов. Используется статистика . Среднее значение этой статистики, имеющейся в расчетной таблице, равно 0,00417. Обращаясь к графику, показанному на рис.12, можно видеть, что данная величина является средним интегральным значением плотности распределения наработки.

5) Нелинейный рост интенсивности отказов и экспоненциальный вид гистограммы наработки позволяет выбрать нормальный закон распределения:

.

В качестве оценки математического ожидания используем выборочную среднюю час. Отметим, что среднее значение весьма близко к 350 – математическому ожиданию модельного распределения.

Для оценки дисперсии используем исправленную выборочную дисперсию (час²),

откуда час. Отметим, что «эмпирическое» среднеквадратическое отклонение близко к модельному значению, равному 35.

Используя найденные оценки дисперсии и математического ожидания, применим табличный процессор EXCEL (оператор «НОРМРАСП») и занесем в расчетную таблицу вероятности теоретического нормального распределения. Построим графики статистического и теоретического распределений:

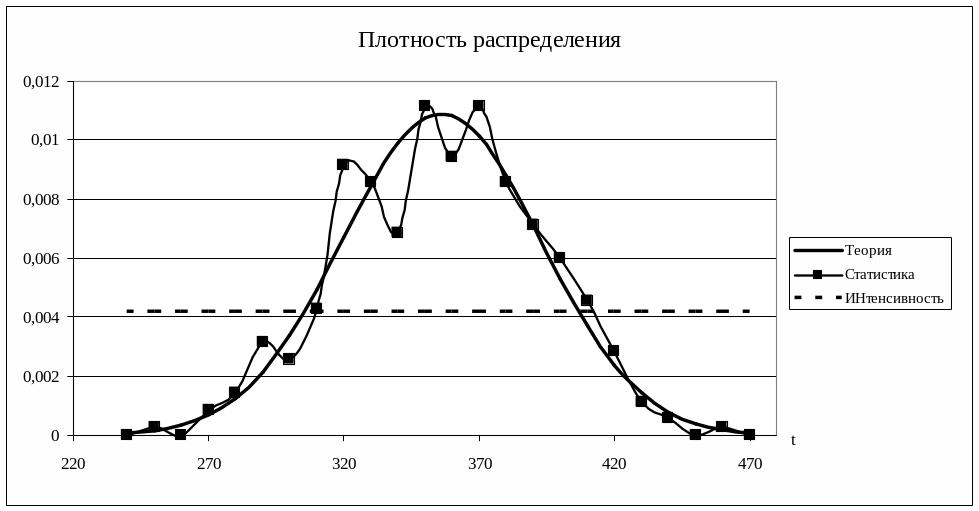
Рисунок 12

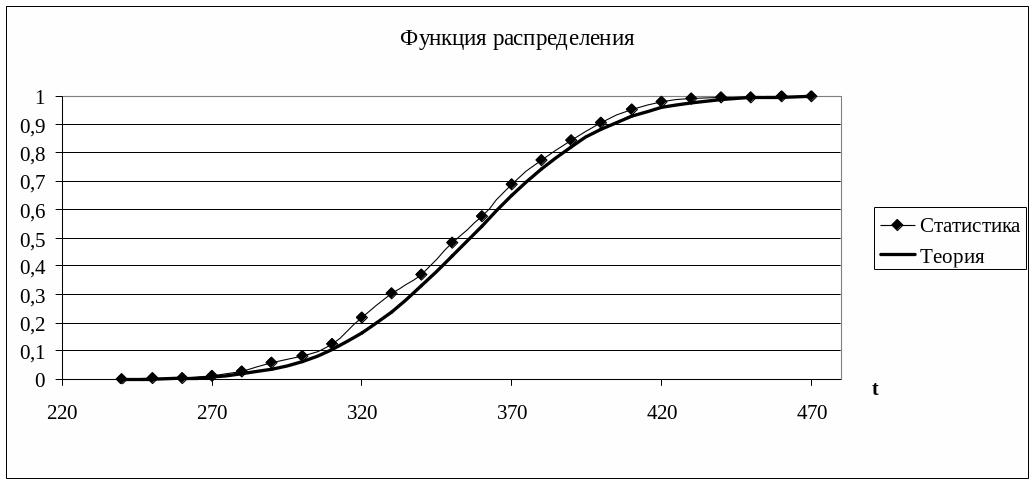
Рисунок 13

Вывод: характер кривых качественно совпадает, но теоретическое распределение несколько смещено назад. В этом, а также в нерегулярности графика эмпирической плотности относительной частоты выражается влияние искусственно внесенной в разделе 1 погрешности «наблюдений».

6) Итак, мы вправе предполагать, что статистическая функции распределения наработки может быть аппроксимирована нормальным распределением с математическим ожиданием =356,086 час и =36,66 час. Подтвердим выдвинутую нулевую гипотезу H₀ с помощью критерия согласия Пирсона.

Для этого вычислим статистику с степенями свободы, где =12 - число интервалов статистического ряда; =2 - число параметров теоретического распределения, вы­численных по статистическим данным (см. таблицу выше). Получаем: .

Применим в MS EXCEL оператор «ХИ2ОБР» и для уровня значимости γ=95% при числе сте­пеней свободы найдем критическое значение =11,6. Так как , т.е. фактически наблюдаемое значение не превышает критиче­ское, гипотеза H₀ о применимости нормального распределения хорошо согласуется со статистическими данными.

7) Пользуясь полученными вероятностными зависимостями, можно определять γ% наработку до отказа.

Применим табличный процессор MS Excel. Например для γ=99%, используя теоретическое распределение

и встроенную функцию «НОРМОБР(0,99;356,086;36,66)», найдем

441,36час

Вычисление вероятности безотказной рабо­ты изделия в течение заданного времени рассмотрим для гарантийного ресурса =400 час. Из оператора «НОРМРАСП(400;356,086;36,66)» следует:

=1-0,079=0,921

Общие выводы

1. В результате проведенной статистической обработки «экспериментальных« данных получены следующие показатели надежности изделий:

- вероятность безотказной работы	0,921
- интенсивность отказов, час-1	=0,00417
- средняя наработка до отказа, час	=356

2. Наработка до отказа составляет 356 час, что заметно меньше гарантийного ресурса 400час. Для повышения безотказности работы гарантийный ресурс должен быть уменьшен, если этого же эффекта не удается достичь конструктивными и технологическими усовершенствованиями изделий.

3. Характерный «стареющий» вид функции распределения и существенно нелинейный рост интенсивности отказов свидетельствуют о том, что отказы связаны с естественным износом изделий. Найденная функция распределения наработки до отказа дает основания для расчета гарантийного срока эксплуатации, при котором будет обеспечена необходимая надежность работы изделий.