Вопрос 3.Метод имитационного моделирования (мим) применительно к задачам систем управления запасами.

Со слов Бродецкого – с его лекции:

Управление запасами используют модели одноразовой загрузки. Существует классическая модель управления запасами.

D – годовое потребление

Cп – стоимость единицы продукции (включает составляющие, зависящие от количества товара)

Co – составляющая расходов на 1 поставку, которая не зависит от количества товара

Ch – годовые издержки хранения 1 ед. товара

q – объем партии товара (размер запаса)

T – период повторения заказа (время между поставками)

Будем считать, что спрос равномерен, нехватку товаров компенсируем страховым запасом

• Формула экономичного размера заказа

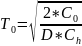
• Формула периода повторения заказа, в годах

• Число 2 мы можем не писать в формуле, если у нас зарезервированы места на складе

Но! Эта формула(Хариса-Уилсона) была выведена давно и тогдашняя экономика не учитывала временную стоимость денег. А мы учтем:

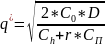
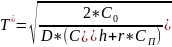
Как пример можем привести задачу с пылесосами, когда если мы возим по 100 пылесосов, у нас на 1 рубль рентабельность почти 100%( конкретнее 96%), а если по 300 – то всего 20% рентабельность. И после этого ЛПР сам решает, что ему выгоднее! Таким образом, мы можем повысить рентабельность производства в три раза.

Задача – построить модель и оптимизировать ее.

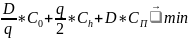
Или относительно Т ( ):

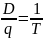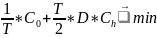
Если мы хотим минимизировать издержки – то оцениваем издержки МИМ.

Если оцениваем рентабельность – то измеряем коэффициент рентабельности.

Иными словами – тут мы рассматриваем метод Монте-Карло, моделируем модель управления запасами, хотим получить число. За год, зная годовое потребление, необходимо минимизировать затраты или максимизировать рентабельность.

Модель разыгрываем столько раз, пока не получим идеал.

Минусы: перебор (иногда может длиться очень долго).

Имитационное моделирование — это метод, позволяющий строить модели, описывающие процессы так, как они проходили бы в действительности. Такую модель можно «проиграть» во времени как для одного испытания, так и заданного их множества. При этом результаты будут определяться случайным характером процессов. По этим данным можно получить достаточно устойчивую статистику. Имитационное моделирование — это метод исследования, основанный на том, что изучаемая система заменяется имитатором и с ним проводятся эксперименты с целью получения информации об этой системе. Экспериментирование с имитатором называют имитацией (имитация — это постижение сути явления, не прибегая к экспериментам на реальном объекте). Имитационное моделирование — это частный случай математического моделирования. Существует класс объектов, для которых по различным причинам не разработаны аналитические модели, либо не разработаны методы решения полученной модели. В этом случае математическая модель заменяется имитатором или имитационной моделью. Цель имитац. эксперимента: проверка выдвинутой гипотезы, оценка реакции моделируемой системы на то или иное воздействие, выявление влияния случайных возмущений на ход процесса и т.д. Далее строится модель, связывающая эндогенные переменные с ее управляющими и экзогенными переменными (напр.: в виде показателей, представленных временными трендами).

Имитационное моделирование (ИМ) применяется в прогнозировании процессов, анализ которых невозможен на основе прямого эксперимента. Процессы взаимодействия между производственными системами, производственными и экологическими системами, распределительные отношения на макроэкономическом уровне. Имитация производится при прогнозировании для согласования различных типов процессов, например, повышения жизненного уровня населения с развитием общественного производства. Проверка и демонстрация новых идей. ИМ есть процесс конструирования модели реальной системы и постановки экспериментов на этой модели с целью либо понять поведение системы, либо оценить (в рамках ограничений, накладываемых некоторым критерием или совокупностью критериев) различные стратегии, обеспечивающие функционирование данной системы.

ИМ предполагает:

1. Выдвижение теорий и гипотез о возможной структуре процесса (системы), характере его связей, о локальных целях развития каждого элемента структуры и глобальной цели развития всей системы;

2. Не всегда процесс можно описать уравнениями (часто связи имеют неформализуемый вид)

3. Определение количественных и качественных закономерностей внутренних и внешних взаимосвязей процесса

4. Имитация развития процесса (поведения системы), прогнозирование на этой основе будущих его состояний.

В узком смысле под ИМ понимают имитацию поведения системы путем воспроизведения взаимодействий ее элементов между собой и с внешней средой (метод Монте-Карло). Структура связей модели предполагается заданной. По сути это модели «черного ящика». Решения получаются в ходе эксперимента в виде конкретных количественных характеристик. ИМ – это не метод, а методология решения проблем.

Сложные имитационные модели используются для получения научно обоснованного представления о возможных тенденциях развития мирового сообщества на период 100-150 лет. Этапы решения проблемы с использованием имитационных моделей:

1. Формулируется проблема

а)определение цели исследования

б)концептуальное описание модели

в)определение возможности проведения имитационного эксперимента по модели

2. Разрабатывается модель

а)построение системы математических уравнений, описывающих развитие объекта

б)разработка программы и ее реализация на ЭВМ

в)оценка адекватности модели

• Логическая проверка соответствия модели исходным предположениям;

• Количественная проверка соответствия между поведением модели и поведением системы;

• Проблемный анализ, основанный на формулировании статистически и содержательно значимых выводов на основе данных, полученных в ходе имитационных расчетов.

3. Планируется эксперимент и способ его проведения

4. Прогнозирование и анализ чувствительности результатов

5. Принятие прогнозного решения (приемлемость прогноза)

Можно выделить две разновидности имитации: Метод Монте-Карло (метод статистических испытаний); Метод имитационного моделирования (статистическое моделирование).

Метод Монте-Карло – это численный метод решения математических задач, ответ на которые формируется в виде числа, а процесс решения основывается на моделировании, разыгрывании случайных величин.

Общая схема метода:

1. Конструируем случайную величину ξ, Мξ=m, Дξ≤B²

2. Формируем наблюдения { ξ ₁,…, ξ _n}

3. 

Под случайными числами понимаются числа, такие что:

1. Каждая очередная запись неизвестна заранее

2. Каждая запись не зависит от предыдущей

3. ξ принимает все допустимые значения с одинаковыми вероятностями

Дискретные СВ: ξ: ξ₁,…, ξ_n с вероятностями p₁,…,p_n

Строим последовательность, удовлетворяющую условиям 1 и2, каждая запись состоит из известных ξ₁,…, ξ_n с вероятностями p₁,…,p_n

Алгоритм:

1. γ, γ<p₁ =>ξ₁, если нет то 2

2. γ<p₁+p₂ =>ξ₂

3. γ<p₁+p₂+p₃ =>ξ₃ и тд

Так как ξ распределена равномерно на (0, 1), то вероятность попасть на интервал из (0, 1) равна длине интервала.

Непрерывные СВ

F(x) - Функция распределения

f(x) - Плотность распределения

Свойства:

1. Случайность

2. Независимость

3. Соответствие ЗР: для любого (t₁, t₂) P{t₁<запись <t₂}=F(t₂)-F(t₁)=

F(ξ)= γ, γ€R(0, 1)

γ – СВ, так как 1 и 2 выполняются

Вероятность, что γ €(t₁, t₂) равна длине интервала

Примеры:

1. Экспоненциальный ЗР

=>

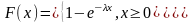
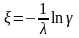
2. Равномерный ЗР

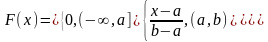
3. Hормальный ЗР сначала генерируем η стандартный нормальный, а затем ξ=m+ση

Моделирование многомерных случайных величин.

Рассмотрим на примере двумерных величин. Разыгрывание сводится к разыгрыванию её составляющих. Если х и у независимы, то находится ЗР каждой из составляющих, которая затем разыгрывается как одномерная, не зависимо от другой. Если х и у зависимы, то находится ЗР одной составляющей и условный ЗР другой.

ДСВ, пример.

У	Х1	Х2	Х3
У1	0,1	0,3	0,2	0,6
У2	0,06	0,18	0,16	0,4
	0,16	0,48	0,36

Ру1/х3=0,2/0,36=5/9

Ру2/х3=0,16/0,36=4/9

Ру1/х1=0,1/0,16=5/8

Ру2/х1=0,06/0,16=3/8

НСВ, пример

Если х и у независимы, то находится ЗР любой из составляющих и разыгрывают произведение методом обратной функции. Если х и у зависимы, то находится ЗР одной составляющей и условный ЗР другой.

Рассмотрим моделирование непрерывной векторной СВ . Ее полное описание задается совместной ПРВ , , где Т - символ транспонирования.

Стандартный метод моделирования векторных СВ основан на представлении w(x) в виде произведения (2.17) частной (маргинальной) ПРВ величины ξ1 и условных ПРВ ξk при условии, что . Из формулы (2.17) следует, что вектор может моделироваться покомпонентно: сначала величина ξ1 с ПРВ , далее - ξ1 по ПРВ и т. д. Последней моделируется m-я компонента ξm , имеющая ПРВ . Стандартный метод требует определенной вычислительной работы, связанной с нахождением условных и частных ПРВ компонент. После вычисления ПРВ каждая компонента моделируется как скалярная величина методами, изложенными выше.

Рассмотрим подробнее процесс моделирования многомерного нормального распределения. Случайный вектор ξ имеет невырожденное n-мерное нормальное распределение, если его ПРВ имеет вид ,(2.18)

где - математическое ожидание ; - заданная симметрическая положительно определенная m*m-матрица; - квадратичная форма x-μ переменных с матрицей . Матрица является ковариационной матрицей вектора ξ; обратная ей матрица B часто называется матрицей точности. Распределение (2.18) полностью описывается двумя параметрами: вектором μ и матрицей R. Далее используется краткое обозначение ξ ~N(μ,R).

Если математическое ожидание равно нулю, а корреляционная матрица R равна единичной матрице I, т. е. ξ ~N(0,I), то распределение называется стандартным нормальным распределением. Стандартное распределение легко моделируется. Для этого нужно положить все компоненты ξ равными независимым реализациям СВ ξ ~N(0,I ).

В общем случае распределение (2.18) моделируется с помощью линейного преобразования . Здесь m*m-матрица определяется разложением ковариационной матрицы R в произведение двух треугольных матриц R=AA^T (2.19)

В уравнении (2.19) будем считать A нижней треугольной матрицей:

В этом случае явный вид коэффициентов определяют следующие уравнения [1, 41]:

, , (2.20)

(2.21)

(2.22)

Плохая обусловленность (вырожденность) матрицы A требует проверки на каждой строке условия , означающего линейную зависимость k-й компоненты вектора ξ. Здесь ε* - малое число. Если это условие выполняется, то нужно положить akk=0, длина k-й строки L(k) совпадает с длиной предыдущей. Индекс l принимает значения 2,3…L(k) его предельное значение L(k) - переменно. Число L(k) является счетчиком числа линейно независимых элементов последовательности . Присвоение L(k) последующего значения L(k+1)=L(k)+1 осуществляется лишь при условии akk>ε*. После расчета последней m-й строки значение L(m) равно рангу матрицы R.

Оценка точности решения имитационных задач.

Оцениваем точность полученного результата, после моделирования СВ следующим образом: определяем необходимый объем выборки для заданной точности. Используем ЦПТ: (*) , ,

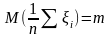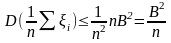
Для (*) выполняется правило трех сигм:

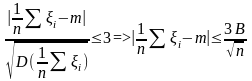
Если n ->∞ , то 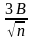->0 а значит, ошибка не превышает

Чтобы найти заданную точность

К наиболее важным задачам при проведение имитационного эксперимента относится задача определения требуемого объема выборки. Следует заметить, что поскольку имитационная модель носит стохастический характер, то точность полученных результатов существенно зависит от объема выборки. Известно также, что многие методы анализа стохастических систем базируются на предположении о том, что распределение случайных величин в таких системах подчиняется нормальному закону, т.к. на основании применения центральной предельной теоремы теории вероятности, отклики в таких системах представляют собой некоторую совокупность “больших” чисел на отклик сложной системы. Это приводит к тому, что отклик носит нормальное распределение. На основании этого эффекта и производится выбор требуемого объема выборки. Оцениваемым параметром, в этом случае, является среднее значение и среднеквадратическое отклонение. При этом используют правило метода доверительных интервалов, в котором предполагается задание точности по двум параметрам: {d_n - m_n} и {b_n - s_n (D =s_n² )}. Для некоторого отклика модели для определения объема выборки необходимо задавать d_n, b_n и a (a - 1), где a - уровень значимости. Требуемый объем выборки должен удовлетворять условиям: Y_n,k - d_n £ M_n £Y_n,k + d_n, D_n,k - b_n £ D £ D_n,k + b_n.

Исследователь обычно задает число опытов слишком большое, однако, на практике рекомендуется следующий алгоритм выбора объема выборки: задают N1 = 5, где N1 - объем выборки и первая итерация заключается в подсчете

Вторая итерация: для очередного номера N выходных сигналов определяют точность b_n1, d_n1 (d_n1 £ d_n, b_n1 £ b_n при уровне значимости a) и проводят эксперимент. Эта оценка может быть оценена тремя способами:

1 способ.

Если объем выборки N1 < 30, то для вычисления доверительного интервала можно воспользоваться Т - статистикой, из которой d_n1 определяется следующим образом:

В этой формуле tкр - значение, определяемое из таблицы распределения Стъюдента или Т-статистики аналогично вопросам адекватности по уровню значимости a (1 - a) и по числу степеней свободы g = N₁ -1.

2 способ.

Если объем выборки N1> 30, то для вычисления доверительного интервала используют двухстороннюю статистику нормированного нормального распределения.

(4)

Z _a/2 = t, Z _a/2 - определяют также из таблиц по заданному уровню значимости.

3 способ.

Если нормальность отклика Y_n,k заранее установить нельзя, то применяется неравенство Чебышева, в котором предполагается, что N₁ > 30.

где Y_n - среднее значение выборки N₁, m_n - математическое ожидание, h - константа, определяющая среднеквадратическое отклонение, которое удовлетворяет исследованию, как правило, n > 1 , тогда доверительный интервал:

или при оценке дисперсии: Р{(1 - b_n) s_n² £ D_n £ (1+b_n) s_n²} = 1 - a,

Третья итерация связана с оценкой полученных значений b_n1, d_1n с заданными: d_n1 £ d_n, b_n1 £ b_n. Если требуемая точность достигается, то процедура переходит к пятому шагу итерации, если нет - к четвертому шагу. Четвертый шаг итерации связан с увеличением начальной выборки N₁ = N₁ +1. Затем осуществляется переход к первому шагу. Пятый шаг - проверяют, все ли компоненты по выходным откликам удовлетворяют точности оценок математических ожиданий и дисперсий и, если эта проверка по всем параметрам дает положительный результат, то эксперимент завершается.