Вопрос 11. Методы многоуровневой оптимизации. Центральная задача в методе Корнаи-Липтака. Экономическое содержание двойственных оценок в этой задаче.

Необходимость решения задач планирования и управления на нескольких последовательных уровнях возникает по причине необходимости сократить непроизводственные потери, а те ресурсы, которые мы имеем, распределить наиболее эффективно, повысить эффективность использования централизованных ресурсов за счет перераспределения этих ресурсов в те подразделения, двойственная оценка которых выше.

Такого рода задачи возникают в различных сферах социальной и экономической жизни на страновом уровне (распределение бюджета между сферами экономики, регионами), на региональном (распределение ресурсов, в том числе денежных), на отраслевом (холдинговом) (всё что хотим, ответственность, риск и пр.). Для уровня предприятия (в котором n-подразделений и m-централизованных ресурсов) известны следующие, получившие широкое распространение методы оптимизации:

Точные: Корнаи-Липтака и Данцинга-Вулфа

Приближенные: метод аппроксимации Пугачева

Особенностью этих методов является направленность информационных потоков. Например, в методе К-Л уровень эффективность централизованного ресурса j (j = 1, … ,m) для предприятия с индексом i (i = 1, … ,n) определяется на нижнем уровне (на уровне конкретного подразделения), а целью центральной задачи является перераспределение централизованных ресурсов в те сектора (предприятия), двойственная оценка которых выше. То есть реализуется идея: «бери, сколько хочешь, но верни адекватно взятому». В методе Д-В идея: «передай нам всё, что ты имеешь, и мы скажем, что ты будешь делать» (здесь выше транзакционные издержки, но и ниже риск).

Постановка задачи:

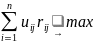
u_i – дв. оц i-го подразделения

r_i – ресурс, выделенный i-му подразделению

Центральная задача решается отдельно для каждого ресурса.

Особенность метода К-Л: мы перераспределяем ресурсы с учетом центральной задач, но не именно так

1. Учитываем центральную задачу

2. обеспечиваем сходимость алгоритма за конечное количество итераций

Пример. Объединение, состоящее из двух предприятий, производит 4 вида продукции. Нормы затрат ресурсов на производство отдельных продуктов, прибыль от их реализации и наличие ресурсов представлены в табл.

Вилы ресурсов	Нормы затрат ресурсов (т/шт.)				Наличие ресурсов (т)
	Предприятие 1		Предприятие 2
	Продукция А	Продукция Б	Продукция В	Продукция Г
1	2	3	—	—		12
2	2	1	—	—		8
3	—	—	1	2		8
4	—	-	2	2		10
5	4	3	1	1		18
6	2	2	4	5		30
Прибыль (р./шт.)	12	6	5	2

Требуется определить оптимальный вариант производственной программы объединения, обеспечивающий получение максимальной прибыли.

Обозначим через хj-объем производства j-го продукта (j=1, 2, 3, 4( А, Б, В, Г)). Тогда модель в численном виде будет выглядеть следующим образом:

• 1) расход собственных ресурсов на предприятии I не превосходит их наличия

2x₁ + 3x₂≤ 12;

2x₁+x₂≤ 8;

• 2) расход собственных ресурсов на предприятии II не превосходит их наличия

x_з + 2x₄ ≤ 8;

2x_з +2x₄ ≤ 10;

• 3) суммарный расход общих ресурсов объединения на пред­приятиях I и II не превосходит лимитов этих ресурсов

4x1+3x2+x3+x4 ≤18

2x1+2x2+4x3+5x4 ≤ 30

• 4)выпуски продукции должны быть неотрицательны

x₁, > 0; х₂ > 0; x₃ > 0; x₄ > 0;

• 5) общий объем прибыли по объединению должен быть макси­мальным

12x₁ + 6x₂ + 5x₃ + 2x₄ →max.

По своей сути задача текущего оптимального планирования на уровне объединения является задачей специализации, в которой требуется определить оптимальный план выпуска продукции (как по объему, так и по составу) при заданных ресурсах. Детальное моделирование процесса выпуска продукции и расходования ресурсов требует включения в модель объединения описания предприятий. Это ведет к большой размерности задачи на уровне объединения и вытекающих отсюда трудностей при ее решении, но одновременно дает и средство для преодоления этих трудностей, а именно: специфический вид матрицы задачи.

Действительно, обращаясь к примеру, видим, что имеется блочная задача линейного программирования, состоящая из 3 блоков, в каждом из которых по 2 ограничения. Условия 1) составляют I блок, условия 2) — II блок. Эти блоки описывают условия функционирования локальных объектов (предприятий), отражая ограниченность локальных ресурсов, т.е. собственных ресурсов предприятий (например, основных фондов разного вида).

Условия 3) составляют III блок. Он характеризует условия функционирования объединения в целом и отражает ограниченность общих ресурсов (например, сырья).

Перейдем к составлению модели в буквенных обозначениях. Для компактности запишем ее в матричном виде. Пусть

t — индекс предприятия, входящего в отрасль (t =1, 2,..., T);

jt,— индекс вида продукции, производимой t-м предприятием

(jt,=1,2,..., nt,);

it, — индекс вида ресурса, «собственного» для предприятия t

i — индекс вида ресурса общих ресурсов объединения (i = 1,2.....тt)

Xt, — вектор выпуска продукции предприятием / (размернос­тью nt х1);

Вt, — вектор лимитов локальных ресурсов i, , потребляемых предприятием t (размерностью т x nt);

В — вектор лимитов общих ресурсов i (размерностью т х 1); Рt, — вектор удельной прибыли от выпуска продукции пред­приятием t (размерностью 1 х п,);

At,— матрица коэффициентов (норм) затрат локальных ресур­сов на выпуск продукции предприятием t (размерностью тt х пt): At — матрица коэффициентов (норм) затрат общих ресурсов на выпуск продукции предприятием t (размерностью т х п,).

В этих обозначениях модель объединения, состоящего из Т предприятий, запишется следующим образом:

А₁X₁ ≤ В₁

АtХt ≤ B_t

…

А_TХ_T ≤ В_T

Р1Х1 + ... + РtХt + ... + Р_ТХ_Т  max.

В нашем примере

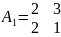
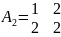
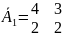
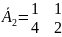
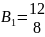
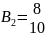
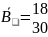
P1= (12, 6)

P2= (5, 2)

Блочная структура задачи текущего планирования на уровне объединения делает возможным ее расчленение на ряд подзадач существенно меньшей размерности и их взаимосвязанное реше­ние в рамках итеративного процесса. Методы решения могут быть различны.

Метод планирования на двух уровнях Корнаи -Липтака

В этом методе итеративный процесс двухступенчатой опти­мизации планов развития объединения и отдельных предприя­тий основан не на корректировке двойственных оценок ресурсов и продукции (как в методе Данцига Вулфа), а на корректировке выделяемых предприятиям лимитов ресурсов и заданий по выпуску продукции в натуральном выражении в соответствии с анализом и сравнением предельных эффективностей (оценок) их использования на предприятиях.

Пусть исходная задача объединения по-прежнему имеет вид блочной задачи как в примере. Проведем посекторное (по предприятиям) разбиение векторов лимитов общих ресурсов.

Разделим оба общих ресурса поровну (первый шаг)между двумя предприя­тиями:

9 + 9= 18; 15+ 15 = 30.

Получаем для первого шага две секторные задачи, их планы, значения прибыли и секторные оценки общих ресурсов .

Решаем 2 задачи симплекс методом отдельно.