3. Задача.

Билет № 7

1.Теорема о пропорциональных отрезках в прямоугольном треугольнике.

Т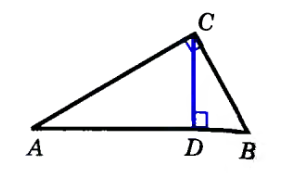 еорема. Высота прямоугольного треугольника, проведенная из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику.

Доказательство.

Пусть ABC — прямоугольный треугольник с прямым углом С, CD — высота, проведенная из вершины С к гипотенузе АВ. Докажем, что ΔABC ΔACD, ΔABC ΔCBD, ΔACD ΔCBD. Треугольники ABC и ACD подобны по первому признаку подобия треугольников (A — общий, ACB=ADC=90°). Точно так же подобны треугольники ABC и CBD (B — общий и ACB = BDC=90°), поэтому A=BCD. Наконец, треугольники ACD и CBD также подобны по первому признаку подобия (в этих треугольниках углы с вершиной D прямые и A=BCD), что и требовалось доказать.

Отрезок XY называется средним пропорциональным (или средним геометрическим) для отрезков АВ и CD, если

Из теоремы имеются следующие утверждения:

1°. Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой.

2°. Катет прямоугольного треугольника есть среднее пропорциональное для гипотенузы и отрезка гипотенузы, заключенного между катетом и высотой, проведенной из вершины прямого угла. ,

Запись на доске.

Дано: ΔАВС - прямоугольный, CD AB

Доказать: ΔABC ΔACD, ΔABC ΔCBD, ΔACD ΔCBD.

Доказательство. ΔABC ΔACD по 1 признаку подобия (A — общий, ACB=ADC=90°).

ΔABC ΔCBD по 1 признаку подобия (B — общий и ACB = BDC=90°), ═>A=BCD.

ΔACD ΔCBD по 1 признаку подобия (ADС = BСD=90°, A=BCD).

Следствия:1)

2) ,

2.Смежные и вертикальные углы. Определение, свойство.

О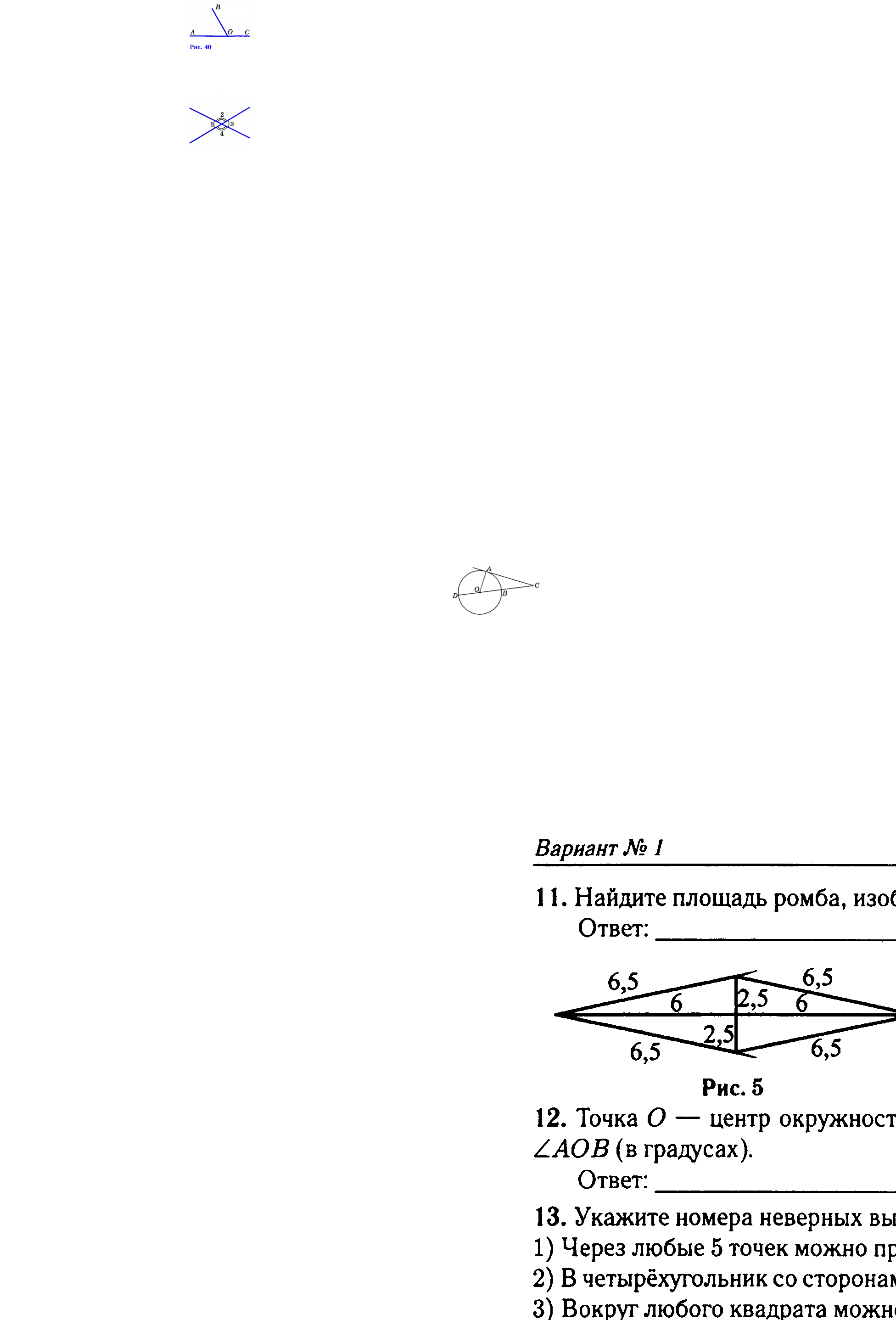 пределение. Два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой, называются смежными

На рисунке углы АОВ и ВОС смежные.

Свойство. Сумма смежных углов равна 180º.

Так как лучи ОА и ОС образуют развернутый угол, то АОВ+ ВОС= АОС=180°.

О пределение. Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого.

На рисунке углы 1 и 3, а также 2 и 4 – вертикальные. Вертикальные углы обладают следующим свойством.

Свойство. Вертикальные углы равны.

3. Задача.

Билет № 8

1. Тригонометрические тождества. Доказательство основного тригонометрического тождества.

В курсе геометрии 8 класса изучается два тригонометрических тождества:

и sin²A +cos²A=1 - основное тригонометрическое тождество.

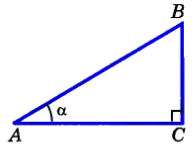
Дано: ∆АВС - прямоугольный, АВ - гипотенуза.

Доказать: sin²A +cos²A=1.

Доказательство: по определению , .

sin²A +cos²A= , так как по т. Пифагора ВС²+АС²=АВ²

запись на доске: аналогично.

2. Равнобедренный треугольник. Определение, свойства, признаки.

Определение: Треугольник называется равнобедренным, если две его стороны равны.

Н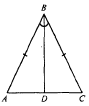 а рисунке равные стороны (АВ=ВС) называются боковыми сторонами, третья сторона АС- основанием равнобедренного треугольника.

Определение: Треугольник все стороны которого равны называется равносторонним.

Равнобедренный треугольник обладает двумя свойствами, которые можно сформулировать в виде теорем.

Теорема 1. В равнобедренном треугольнике углы при основании равны.

В равнобедренном треугольнике АВС с основанием ВС В= С

Теорема 2. В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой.

В равнобедренном треугольнике АВС с основанием ВС AD - биссектриса => AD – медиана, высота.

Справедливы 2 следствия из теорем

1: Высота равнобедренного треугольника, опущенная на основание, является медианой и биссектрисой.

2: Медиана равнобедренного треугольника, проведенная к основанию, является высотой и биссектрисой.

Признак: если два угла треугольника равны, то треугольник равнобедренный.

3. Задача

Билет № 9