3. Задача.

Билет № 4

1. Признаки параллельности двух прямых.

Существуют 3 признака параллельности двух прямых:

1 ) Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.

Прямые a и b пересечены прямой. Если выполняется хотя бы одно их следующих условий: 4=6; 3=5, то согласно признаку 1, a║b.

2) Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.

Если выполняются хотя бы одно из условий: 1=5; 2=6; 4=8; 3=7, то по признаку 2 прямые a║b.

3) Если при пересечении двух прямых секущей сумма односторонних углов равна 180º, то прямые параллельны.

Если выполняется хотя бы одно из условий 4+5=180º; 3+6=180º, то по признаку 3 прямые параллельны a║b.

Докажем 1-ий признак: Пусть при пересечении прямых а и b секущей АВ накрест лежащие углы равны: 1=2. Докажем, что a||b. Если углы 1 и 2 прямые, то прямые а и b перпендикулярны к прямой АВ и, следовательно, параллельны. Рассмотрим случай, когда углы 1 и 2 не прямые. Из середины О отрезка АВ проведем перпендикуляр ОН к прямой а. На прямой b от точки В отложим отрезок ВН₁ равный отрезку AH, как показано на рисунке, в, и проведем отрезок OH₁. Треугольники ОНА и ОН₁В равны по двум сторонам и углу между ними (АО = ВО, АН=BH₁ 1=2), поэтому 3=4 и 5=6. Из равенства 3=4 следует, что точка Н₁ лежит на продолжении луча ОН, т. е. точки Н, О и Н₁ лежат на одной прямой, а из равенства 5=6 следует, что угол 6— прямой (так как угол 5 — прямой). Итак, прямые а и b перпендикулярны к прямой HH₁ поэтому они параллельны.

Запись на доске.

Д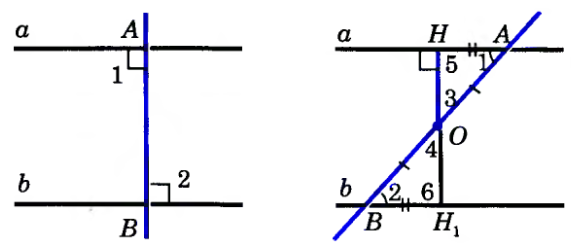 ано: а,b – прямые, АВ – секущая, 1=2 – накрест лежащие

Доказать: а || b

Доказательство. 1) 1=2=90⁰ ═> а AB и b AB ═> а || b.

2) 1=2≠90⁰. О середина АВ. ОН а. Доп. построение: ВН₁ = AH, OH₁.

ΔОНА =ΔОН₁В (по 1 признаку.) (АО = ВО, АН=BH₁ 1=2) ═>

3=4 ═> Н, О и Н₁ лежат на одной прямой

и 5=6=90⁰ Итак, прямые а HH₁ и b HH₁ ═> а || b

2. Окружность. Определение, взаимное расположение прямой и окружности.

О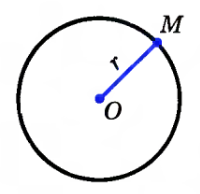 пределение. Окружностью называется геометрическая фигура, состоящая из всех точек, расположенных на заданном расстоянии от данной точки. Эта данная точка называется центром окружности.

Отрезок, соединяющий любую точку окружности с её центром, называется радиусом. Все радиусы имеют одну и ту же длину.

Отрезок, соединяющий две точки окружности, называется хордой.

Х орда проходящая через центр окружности называется диаметром. Диаметр окружности равен удвоенному радиусу.

Существует 3 случая взаимного расположения прямой и окружности в зависимости от соотношения между радиусом r окружности и расстоянием d прямой от центра окружности.

1) d<r. Если расстояние от центра окружности до прямой меньше радиуса окружности, то окружность и прямая имеют две общие точки.

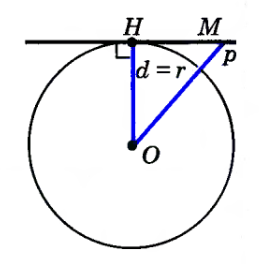
2) d=r. Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют единственную общую точку.

3) d>r. Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек.

З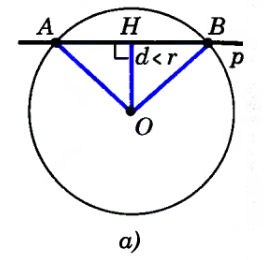 апись на доске.

1) если d<r, то 2 точки

2) если d=r, то 1 точка

3) если d>r, то нет точек