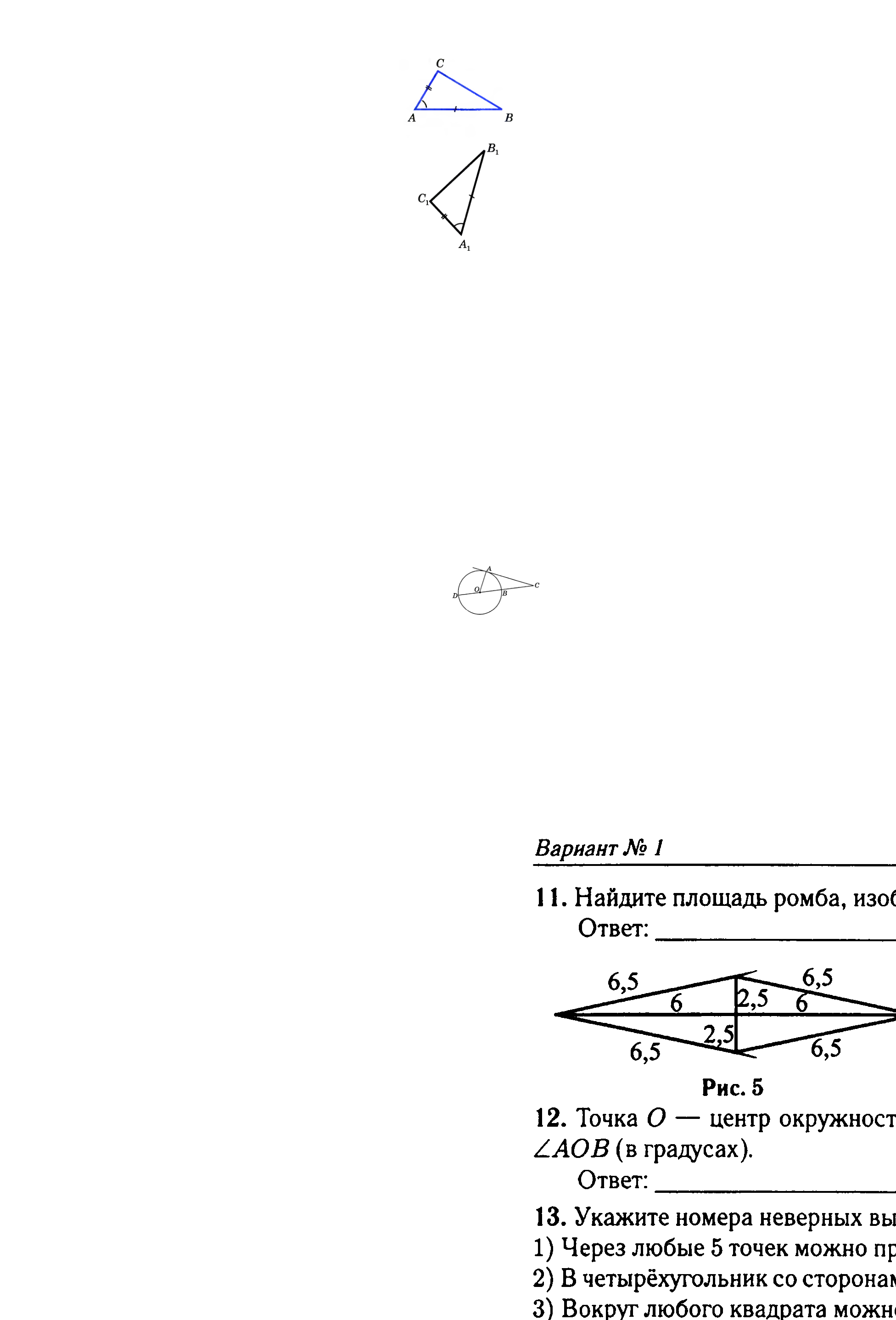Б илет № 1

1. Первый признак равенства треугольников.

Первый признак равенства треугольника по двум сторонам и углу между ними формулируется в виде:

2. Параллелограмм. Определение, свойства, признаки.

Определение. Параллелограммом называется четырёхугольник, у которого противоположные стороны попарно параллельны.

Четырехугольник ABCD имеет стороны AB║DC, а сторона BC║AD. Следовательно ABCD –параллелограмм. АС и ВD – диагонали параллелограмма.

С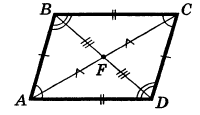 войства:

1) В параллелограмме противоположные стороны равны и противоположные углы равны (AB=DC, BC=AD, A=C, B=D).

2) Диагонали параллелограмма точкой пересечения делятся пополам (BF=FD, AF=FC).

3) сумма углов, прилежащих к одной стороне равна 180⁰ (A+В= С+D=В+C=А+D=180⁰)

Признаки:

1) Если в четырёхугольнике две стороны равны и параллельны, то этот четырёхугольник – параллелограмм.

2) Если в четырёхугольнике противоположные стороны равны, то этот четырёхугольник – параллелограмм.

3) Если в четырёхугольнике диагонали пересекаются и точкой пересечения делятся пополам, то он параллелограмм.

Запись на доске:

Свойства:

1) AB=DC, BC=AD, A=C, B=D.

2) BF=FD, AF=FC.

3) A+В= С+D=В+C=А+D=180⁰)

Признаки:

1) Если ABСD - четырёхуг., и AB║DC и AB=DC, то – ABСD парал-м.

2) Если ABСD - четырёхуг., и AB=DC, BC=AD, то – ABСD парал-м.

3) Если ABСD - четырёхуг., и BF=FD, AF=FC, то – ABСD парал-м..

3. Задача.

Билет № 2

1.Второй признак равенства треугольников.

Второй признак равенства треугольника по стороне и двум прилежащим к ней углам формулируется в виде теоремы.

Теорема: Если сторона и два прилежащие к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника то такие треугольники равны.

2. Прямоугольник. Определение, свойства, признаки.

Определение. Прямоугольником называется параллелограмм, у которого все углы прямые.

Н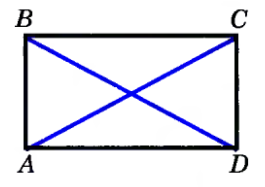 а рисунке изображён параллелограмм ABCD у которого A=B=C=D=90º. АС и ВD – диагонали прямоугольника

Согласно определению этот параллелограмм – прямоугольник. Для него справедливы все свойства и признаки параллелограмма:

Свойства:

1) Противоположные стороны прямоугольника равны (AB=DC, BC=AD).

2) Диагонали точкой пересечения делятся пополам (BО=ОD, AО=ОC).

3)Диагонали прямоугольника равны. (АС=DВ) (особое свойство прямоугольника).

Признак:

1) если в параллелограмме диагонали равны, то этот параллелограмм прямоугольник.

2) Если в параллелограмме один угол прямой, то этот параллелограмм – прямоугольник.

Запись на доске:

Свойства:

1) AB=DC, BC=AD.

2) BО=ОD, AО=ОC.

3) АС=DВ

Признак:

1) Если ABСD – парал-м, и АС=DВ, то – ABСD - прямоугольник.

2) Если ABСD - парал-м., и A=90⁰, то – ABСD прямоугольник.

3. Задача.

Б илет № 3

1. Третий признак равенства треугольников.

Третий признак равенства треугольников по трем сторонам формулируется в виде теоремы.

Теорема: Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.