2.2.2 Решение уравнения движения

Из выражений сил, приложенных к поезду, очевидно, что их равнодействующая

зависит от скорости.

Если в числе сил, определяющих движение системы, имеется хотя бы одна сила, зависящая от скорости, то рассчитать движение с помощью общих теорем классической механики нельзя потому, что такие силы проявляются в процессе движения и, влияя на кинематические характеристики движения, сами не линейно зависят от них. Расчет движения ставится в форме задачи Коши: найти численную зависимость v(t) за период времени от t₀ до t_n, если известна начальная скорость движения v₀ в начальный момент времени t_Q, и равнодействующая сила является некоторой заданной функцией времени и скорости/_д =(p(/,v). Такие задачи можно

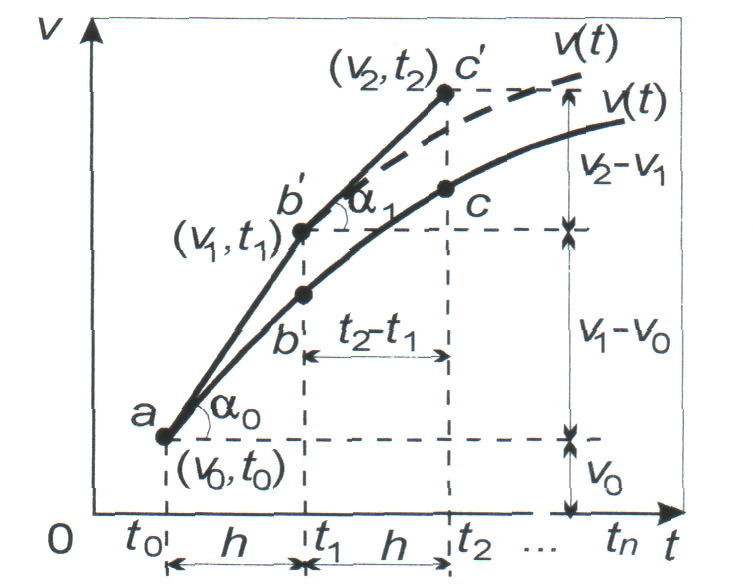
решить только методом интегрирования дифференциального уравнения движения. Из многих известных методов (Чаплыгина, Адамса, Рунге-Кутта, Милана и др.) в тяговых расчетах используется чаще всего метод Эйлера. Суть этого метода заключается в аппроксимации интегральной кривой v(/) последовательно сопряженными касательными.

Запишем уравнение движения (2.1) в виде задачи Коши [3]:

(2.17)

при начальных условиях v(t₀)= v₀.

Период времени [t₀, t ] разделим на п равных частей и обозначим шаг вычислений (шаг интегрирования)

Считая правую часть уравнения (2.18) постоянной в пределах каждого интервала (шага интегрирования), производную в каждой точке кривой v{t) заменим отношением конечных разностей

(2.18)

Для каждого шага вычислений

при

при

при

Такая замена равносильна тому, что искомая функция на шаге [ti,t,+h] заменяется касательной, например, для интервала [ ] касательная аЪ'

образующая с осью времени угол , тангенс которого равен

Рис.2.2 Построение ломаной Эйлера

(рис.2.2) Для следующего шага (t₂-t₁)касательная проводится к кривой v(t), но не от точки Ъ, а от точки Ь\ т.о. имеем касательную b'с'. Ряд сопряженных касательных образует «ломаную Эйлера». Для вычисления фазовых координат поезда перепишем конечные разности на отрезках, разрешенные по скорости в концах интервалов

(2.19)

Таким образом, по заданным v₀,t₀,h и известному значению равнодействующей силы q>₀(t₀,v₀) на первом шаге определяется значение v,. Затем по полученным на предыдущем шаге v_x,t_vh и ф,(/|,у,) определяем v₂ и т.д. В итоге по выражениям (2.20) определяется скорость на всем интервале времени [ ].

При интегрировании по скорости уравнения

ds - vdt

найдем проходимый поездом путь

(2-20)

…………………..

Расчет времени производится по формуле

(2.21)

Расчет конкретных кривых движения осуществляется с помощью программы Potyag.

2.3 Расчет электромеханических параметров АТД.

2.3.1 Мощность подводимая к АТД

где U„, - номинальное линейное напряжение; [В]

I_nf - номинальный ток фазы; [А]

cos _n - коэффициент мощности АТД;

2.3.2 Мощность реализуемая АТД

P₂= [кВт]

где - коэффициент полезного действия АТД;

2.3.3 Потери мощности

Р = Р₁-Р₂; [кВт]

2.3.4 Электрические потери в обмотке статора

; [кВт]

2.3.5 Потери в стали статора

Р = ; [кВт]

2.3.6 Электромагнитная мощность АТД

; [кВт]

2.3.7 Номинальные обороты ротора

[об/мин]

где f_]n - номинальная частота тока статора; [Гц]

р - число пар полюсов;

2.3.8 Электромагнитный момент АТД

М_э = [Нм]

2.3.9 Напряжение фазы АТД

; [В]

2.3.10 ЭДС асинхронного двигателя в номинальном режиме

E = 0,96·U_nf ; [В]

2.3.11 Поток магнитной системы АТД

Ф = ; [Вб]

где w, - число витков фазы статора;

к_об1 - обмоточный коэффициент фазы статора;

2.3.12 Индукция в магнитном зазоре

; [Тс]

где ; [м] - полюсное деление АТД;

l_С - рабочая длина статора; [м] D_c - диаметр расточки статора; [м]

2.3.13 Индукция в зубце статора

[Тс]

где - ширина коронки зубца статора; [м] - число пазов статора;

k_c - коэффициент заполнения стали статора;

2.3.14 По кривой намагничивания стали находим коэффициент насыщения стали ;

2.3.15 Магнитное напряжение магнитного зазора

; [A]

где - рабочий зазор АТД; [мм] k - коэффициент Картера;

2.3.16 МДС обмотки статора на пару полюсов

F_H=2·F ·k ; [A]

2.3.17 Намагничивающий ток АТД

^{; [А]}

где m – число аз АТД;

18. Частота тока ротора

где ₂ - активное сопротивление фазы ротора; [Ом]

z₂ - число пазов ротора; k = 1,05 1,11 - коэффициент формы поля;

18. Угол между векторами тока и ЭДС ротора

;

где - приведенное активное сопротивление фазы ротора; [Ом] - приведенное индуктивное сопротивление фазы ротора; [Ом]

; ;

Согласно источникам, cos лежит в пределах 0,99 0,98.

2.3.20 Ток ротора, приведенный к току обмотки статора

; [А]

2.3.21 Ток фазы статора

; [А] где ;[A] - активная составляющая тока статора;

; [А] - реактивная составляющая тока статора;

2.3.22 Коэффициент мощности для первой гармоники тока

cos ;

2.3.23 Частота вращения ротора

;[_об/_мин]

где /j - частота тока статора; [Гц]

2.3.24 Скорость движения тепловоза

; [км/ч]

где - диаметр колеса тепловоза; [м]

-передаточное отношение зубчатой передачи тягового редуктора;

2.3.25 Момент на валу АТД

М₂= ; [Нм]

где ; [кВт] - основные электрические потери в обмотке ротора;

; [кВт] - механические потери АТД с независимой вентиляцией;

; [кВт] - добавочные потери в обмотках статора и ротора от высших гармоник тока;

2.3.26 Касательная сила тяги на ободе колеса тепловоза

; [кН]

2.3.27 Касательная сила тяги тепловоза

F_K=K_dv-F; [кН]

где K_dv - количество тяговых электродвигателей тепловоза;

Расчет конкретных кривых движения осуществляется с помощью программы PotyagA.

2.4 Определение тока тягового генератора и расхода топлива дизелем

Тепловоза

Ток, потребляемый тепловозом

; [A]

где I_dv - ток тягового электродвигателя; [А]

К_ггр - кпд преобразователя частоты;

При движении в интервалах времени, соответствующих режимам выбега и торможения, значения токов 1_е1, потребляемых электродвигателями приравнивается к нулю.

Расход топлива определяется для данного двигателя согласно аппроксимированному полиному

(-l,4498e-12^s|:obkol^A5+4,6782e-9*obkol^A4-5,792e-6*obkol^A3+0,0034975*obkol^A2-1,1101 *obkol+322,85)/3600

где obkol-обороты коленчатого вала дизеля, [об/мин];

Обороты коленчатого вала рассчитываются исходя из текущей мощности дизеля тепловоза согласно аппроксимирующему полиному

3,6606e-19*Ptep^A7-2,9586e-15*Ptep^A6+9,7182e-12*Ptep^A5-l,6666e-8*Ptep^A4+l,5933e-5*Ptep^A3-0,0083656*Ptep^A2+2,4169*Ptep+157,01

где Ptep - текущая мощность дизеля тепловоза; [кВт]

Расчет тока и потребленного топлива для решения конкретной задачи осуществляется с помощью программы PotyagA.

2.5 Описание и расчет режимов работы АТД

Р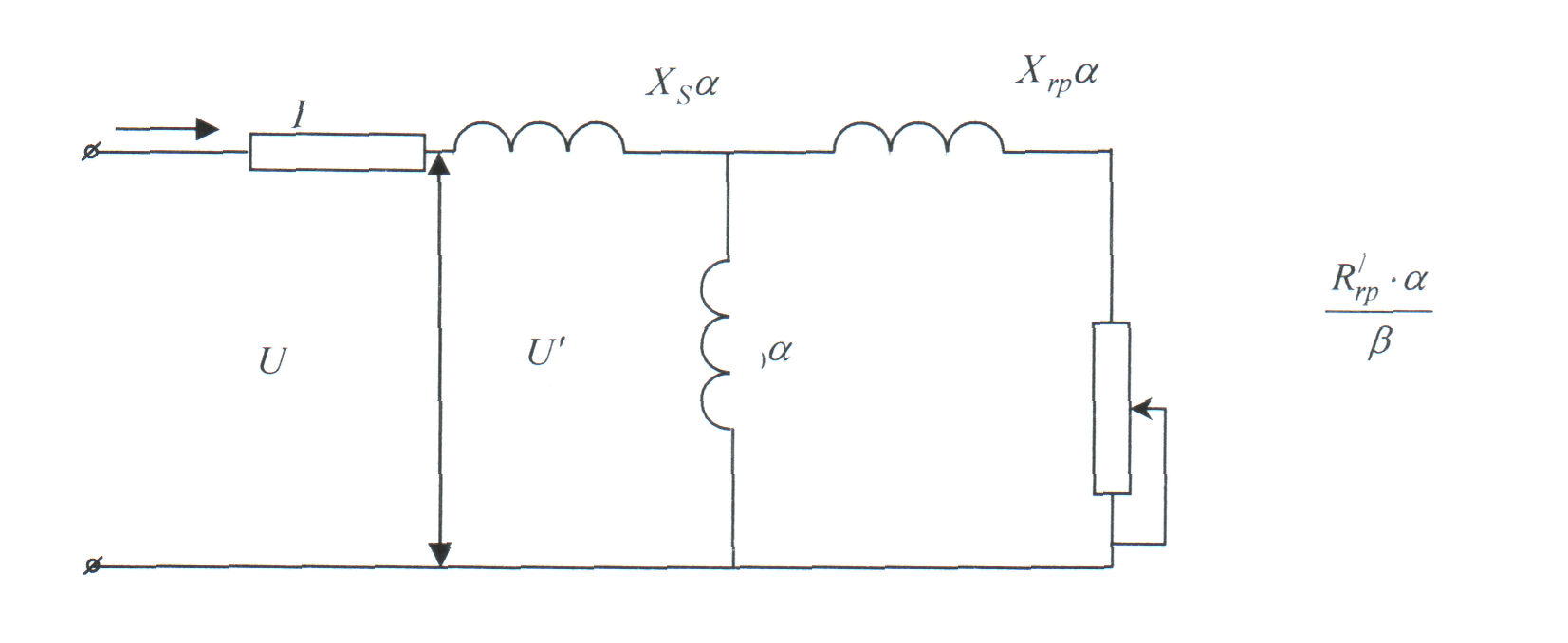 асчет характеристик, определяющих режимы работы асинхронного двигателя при частотном управлении, произведем, используя схему замещения.

где

а - относительная частота тока статора; отношение частоты тока статора к ее номинальному значению:

(3 - относительная частота тока ротора; отношение частоты тока ротора к номинальной частоте тока статора:

у - относительное напряжение на статоре; отношение текущего значения напряжения питания АД к его номинальному значению.

Пренебрегая влиянием насыщения магнитной цепи двигателя и падением напряжения в активных сопротивления статора, академиком Костенко М.П. была выведена зависимость:

или в относительных единицах:

где - относительный момент; отношение текущего значения момента двигателя к его номинальному значению.

Физический смысл приведенной зависимости сформулировал сам М.П.Костенко так: «Если сконструировать асинхронный двигатель для частоты /„ , момента м_и и напряжения на зажимах и_н и изменять затем при новом значении момента м напряжение U частоту /таким образом, чтобы удовлетворилось соотношение:

то двигатель будет работать при практически неизменных cos<?, коэффициенте перегружаемости и абсолютном скольжении, а его кпд будет зависеть только от изменения частоты / и практически не будет зависеть от момента на валу, если насыщение магнитной цепи двигателя не слишком велико».

Для приведения зависимости можно получить несколько ее частных реализаций. Рассмотрим две важные для тягового привода.

При постоянном моменте, что важно при разгоне поезда, т.е. для

м = м_п;

получим

т.е. .

При постоянной мощности, т.е. для режима, характеризующего движение после

разгона

т.е. ;

Таким образом, в режиме пуска, т.е. в диапазоне изменений частоты тока статора от 0 до f_n напряжение целесообразно изменять пропорционально частоте тока статора (или скорости движения тепловоза). При этом магнитный поток, вращающий момент и сила тяги двигателя сохраняются неизменными, а ЭДС двигателя растет пропорционально скорости движения.

По окончании пуска, т.е. при достижении частоты тока статора значения f_n, желательно с точки зрения эксплуатации, иметь постоянную мощность тепловоза. В этом случае, для обеспечения условия Р = const, питающее напряжение следует увеличивать в 77 раз • Однако такой закон увеличения напряжения использовать нецелесообразно, так как двигатель должен быть изготовлен на более высокое напряжение, что ухудшает масса - габаритные показатели как самого двигателя, так и преобразователя частоты. Мощность преобразователя получится завышенной и не сможет быть реализована при максимальной скорости движения по условию ограничения силы тяги по сцеплению колес тепловоза с рельсами. Поэтому целесообразно при условии постоянства мощности тягового двигателя иметь неизменное значение питающего напряжения. Но при постоянстве мощности тягового двигателя, постоянстве питающего напряжения и постоянстве магнитного потока нельзя обеспечить изменение силы тяги обратно пропорциональное частоте

тока статора. Поэтому приходится отказаться от постоянства потока и регулировать его, изменяя ток двигателя так, чтобы выдержать условие постоянства мощности.

Если выбрать мощность преобразователя так, чтобы при условии постоянства напряжения питания, он обеспечивал реализацию заданной силы тяги, равной номинальной, при скорости определяемой предельной силой тяги по сцеплению колеса с рельсом, то можно реализовать силу тяги большую, чем ограниченную условием постоянства мощности двигателей. Такой режим обеспечивается стабилизацией тока двигателя посредством регулирования частоты тока ротора.

Таким образом, при управлении движением тепловоза возникают следующие режимы работы асинхронного тягового двигателя:

• режим разгона - управляющие параметры: частота тока статора и, изменяющиеся по определенному закону исходя из частоты, напряжения питания двигателя при номинальном фазном токе, моменте и частоте тока ротора двигателя;

• режим постоянной тяги - управляющие параметры: частота тока статора и частота тока ротора при заданном токе двигателя, а также при номинальном напряжении питания и постоянном моменте двигателя;

• режим постоянной мощности - управляющие параметры: частота тока статора при постоянном напряжении питания и постоянной частоте тока ротора.

Для установления количественных соотношений введем обозначения:

коэффициент рассеяния статора: коэффициент рассеяния ротора:

общий коэффициент рассеяния:

Кроме того, введем следующие обозначения

2.5.1 Управление с компенсацией падения напряжения в первичных активных

сопротивлениях.

Основной недостаток пропорционального частотного управления и = а-и„ состоит в уменьшении магнитного потока от АТД с понижением частоты питания из-за падения напряжения в первичных активных сопротивлениях статора и преобразователя частоты. Этот недостаток можно устранить, если регулировать напряжение так, чтобы падение напряжения в первичных сопротивлениях точно компенсировались. Для этого необходимо регулировать пропорционально частоте напряжение не на зажимах статора, а внутреннее напряжение эквивалентной схемы замещения (рис. ), т.е.

u' = u-i·r_s; U' = a·U„'.

Т огда закон регулирования первичного напряжения на зажимах статора [ ]