Кратные интегралы

Вариант №1

1. Построить область интегрирования, изменить порядок интегрирования в интеграле:

а) f (x, y) dy; б) .

2. Вычислить а) x sin (x+y) dx dy, если D: 0 x , 0 y /2;

б) dx dy, если D: x = 2, y = x, xy = 1

3. Преобразовать к полярным координатам и вычислить:

dx dy, где D – круг: x² + y² ax;

4. Найти массу пластинки D, если плотность = x² + 2y и

D: y² = 2x, x = 2, y = 0.

5. Найти координаты центра тяжести однородной фигуры, ограниченной линиями:

r = a (1 + cos )

6. Вычислить (x + 2z) dx dy dz , если V: z = x² + 3y² , z = 2.

7. Преобразовать к цилиндрическим координатам и вычислить

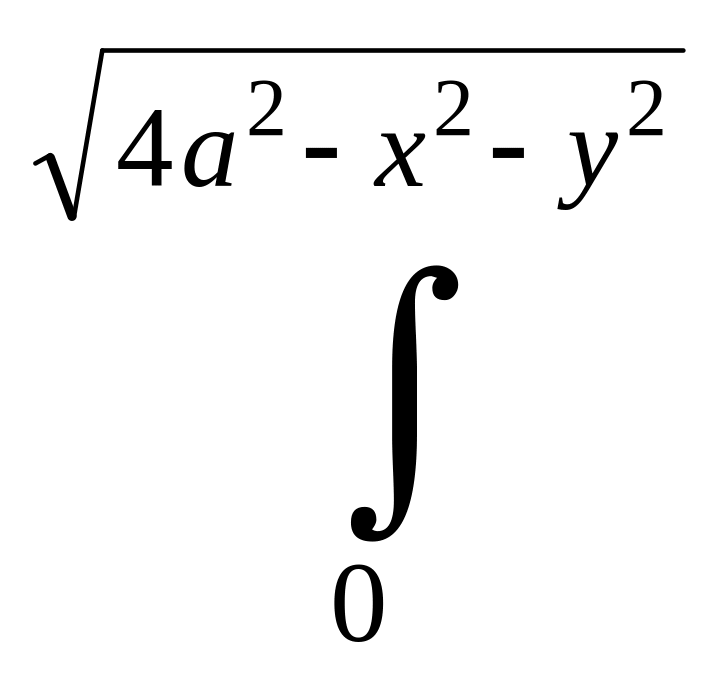dz.

8. Преобразовать к сферическим координатам и вычислить

dx dy dz , если V – шар x² + y² + z² x.

9. Найти объём тела, ограниченного поверхностями:

y = , y = 2 , x + z = 6, z = 0.

10. Найти координаты центра тяжести однородного тела, ограниченного поверхностями x² + y² = 2z , z = 2.

Вариант №2

1. Построить область интегрирования, изменить порядок интегрирования в интеграле: а) ; б) .

2. Вычислить а) соs (x+y) dx dy ; если D: x = 0, y = , y = x.

б) e^x dx dy , если D: x = 0, y = 2 , y = e^x.

3. Преобразовать к полярным координатам и вычислить

e^x dx dy, если D: x² + y² = 4x , y + x .

4. Найти массу пластинки D, если плотность =7x² + y ,

D: y² = 4x , x = 1 , y = 0

5. Найти координаты центра тяжести однородной фигуры, ограниченной линиями r = (1 – cos )

6. Вычислить y cos(z+x) dx dy dz , если V: y = , у = 0, x + z = , z = 0.

7. Преобразовать к цилиндрическим координатам и вычислить

.

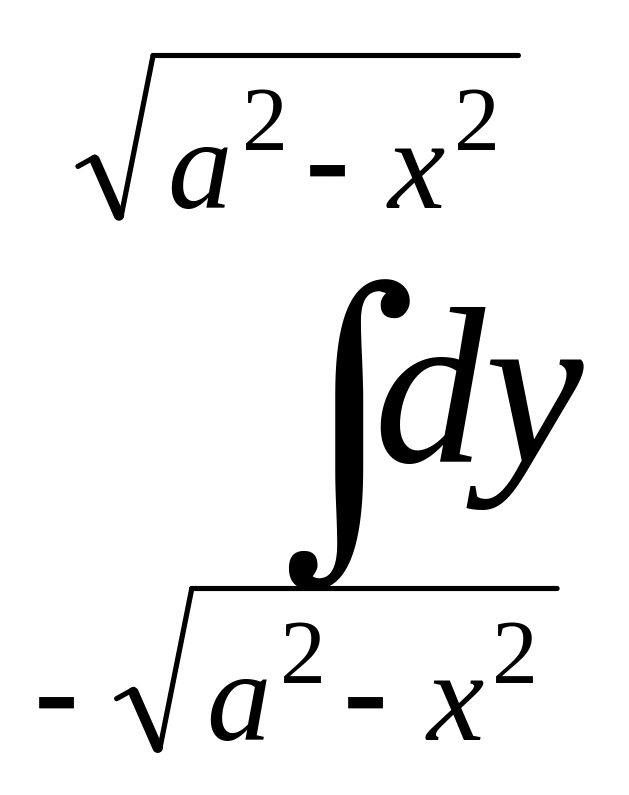
8. Преобразовать к сферическим координатам и вычислить:

dx dy dz , если V – шар x² + y² + z² z.

9. Найти объём тела, ограниченного поверхностями (внутри конуса)

x² + y² + z² = 25, x² + y² + z² = 36, x² + y² z².

10. Найти координаты центра тяжести однородного тела, ограниченного поверхностями: x² + y² = 2z, z = 2.

Вариант №3

1. Построить область интегрирования, изменить порядок интегрирования в интеграле: а) f(x, y) dx; б) .

2. Вычислить а) (x + 2y) dx dy , если D: y² = x + 4 , x = 5;

б) dx dy , если D: x² + y² 1, x , y 0.

3 Преобразовать к полярным координатам и вычислить

(y +1) dx dy , если D: x² + y² = y ;

4. Найти массу пластинки D, если плотность = 5x² + y , D: y² = 4x , x = 1 , y = 0.

5. Найти координаты центра тяжести однородной фигуры, ограниченной линиями r = a (1 – sin ).

6. Вычислить (3x+6y) dx dy dz , если V: z = x² + y², z = 0, y = x ,y = 0, x = 1.

7. Преобразовать к цилиндрическим координатам и вычислить

dx dy (x² + y²) dz.

8. Преобразовать к сферическим координатам и вычислить:

dx dy dz если V – шар x² + y² + z² z, z .

9. Найти объём тела, ограниченного поверхностями:

x² + y² = 4x, z = 4 - y², z = 0.

10. Найти координаты центра тяжести однородного тела, ограниченного поверхностями: y² + z² = 3x, x = 3.

Вариант №4

1. Построить область интегрирования, изменить порядок интегрирования в интеграле: а) f(x, y) dy; б) f(x, y) dх.

2. Вычислить а) x dx dy , если D: y+ x 2 , x² + y² 2y;

б) e dx dy , если D: x = y², x = 0, y = 1.

3 Преобразовать к полярным координатам и вычислить

(x +1) dx dy , если D: x² + y² = x;

4. Найти массу пластинки D, если плотность =x + 3y², D: x² = 2y , x 0 , y = 2

5. Найти координаты центра тяжести однородной фигуры, ограниченной линиями r = a (1 + sin ).

6. Вычислить (x+y) dx dy dz , если V: z = 30x² + 60y²,z = 0,y = x , y = 0, x = 1.

7. Преобразовать к цилиндрическим координатам и вычислить

dx dy (x² + y²) dz.

8. Преобразовать к сферическим координатам и вычислить:

dx dy dz , если V – шар x² + y² + z² + z = 0.

9. Найти объём тела, ограниченного поверхностями:

x = 0, y = 0, z = 0, x + y = 2, z + y² = 4.

10. Найти массу тела плотностью =z, ограниченного поверхностями:

x² + y² + z² 4, x² + y² 3, z 0.

Вариант №5

1. Построить область интегрирования, изменить порядок интегрирования в интеграле: а) dx f(x, y) dy; б) .

2. Вычислить а) dx dy , если D: x = 1, x = 4, y = x, y = 2x;

б) (x² + y) dx dy , если D: x² + y² = ².

3 . Преобразовать к полярным координатам и вычислить:

(x - 2) dx dy , если D: x² + y² = 4x , x + y 0.

4. Найти массу пластинки D, если плотность = y² + 2x и D: x = 0, y² = 4 – x.

5. Найти координаты центра тяжести однородной фигуры, ограниченной линиями x y = 5, x + y = 6.

6. Вычислить x sin (z + y) dx dy dz , если V: x = , x = 0, z = 0, y + z = .

7. Преобразовать к цилиндрическим координатам и вычислить

dx dy (x² + y²) dz.

8. Преобразовать к сферическим координатам и вычислить:

, если V: x² + y² + z² 2z, x 0.

9. Найти объём тела, ограниченного поверхностями:

x = 0, z = 0, x – y = 3, 2z = 9-y².

10. Найти массу тела плотностью = 2y, ограниченного поверхностями:

x² + y² + z² 4, x² + z² 2, y 0.

Вариант № 6

1. Построить область интегрирования, изменить порядок интегрирования в интеграле: а) f(x, y) dy; б) f(x, y) dx.

2. Вычислить а) (12x²y²+16x³y³) dx dy , если D: x = 1, y = x², y = - ;

б) ye dx dy , если D: y = ln2, y = ln3, x = 2, x = 4.

.3 Преобразовать к полярным координатам и вычислить

(x – 1) dx dy , если D: x² + y² - 2ay , y x.

4. Найти массу пластинки D, если плотность =7x²y³,

D: 4x² + 9y² = 36, x , y .

5. Найти координаты центра тяжести однородной фигуры, ограниченной линиями y = 4 – x², y = 0.

6. Вычислить x²z cos x y dx dy dz , если V: x = 1, y = 2x, y = 0, z = 0, z = 3.