Глава 9 Интегральные уравнения специального вида – потенциалы. Сведение краевых задач к интегральным уравнениям

§1. Объемный потенциал

п.1. Из курса общей физики известно, что потенциал u(M) электростатического поля, создаваемого точечным электрическим зарядом величины e, расположенным в точке трехмерного пространства, определяется в точке М выражением (это определение потенциала)

Замечание. Потенциал (или потенциальная функция) электростатического поля – это такая функция, которая определяет силовое поле выражением

Если точечные заряды e₁, e₂, …, e_n расположены соответственно в точках Р₁, Р₂, …, Р_n, то потенциал u(M) в точке М определяют по формуле

(1)

Пусть – плотность распределения зарядов в области D (заряд/объем). В малом объеме заключен заряд величиной Тогда потенциал поля, созданного зарядами, расположенными непрерывно в области D,

(2)

Это объемный потенциал Ньютона. В двухмерном случае имеем «плоский» потенциал

(3)

При Р = М имеем особенность. Таким образом, потенциал является несобственным интегралом.

п.2. Рассмотрим интеграл общего вида

(4)

где точка играет роль параметра, т. е. выражение (4) есть интеграл по параметру.

Определение. Интеграл (4) называют равномерно сходящимся в окрестности точки , если для можно указать такое число , что 1) для всякой области , содержащей точку , с диаметром, меньшим , и 2) для всех точек для которых расстояние , выполнится неравенство

Равномерность – значит точка М играет роль параметра для несобственного интеграла (4).

Теорема. Несобственный интеграл (4), равномерно сходящийся в окрестности точки М₀, непрерывен в этой точке.

Доказательство теоремы приводится в курсе математического анализа, в разделе "Несобственные интегралы, зависящие от параметра".

Свойства объемного потенциала. Пусть Тогда

1. Объемный потенциал определен и непрерывен всюду.

Это следует из теоремы.

2. Объемный потенциал имеет всюду непрерывные частные производные первого порядка по координатам точки М.

Доказательство. Если то свойство очевидно. Если , то достаточно доказать равномерную сходимость в окрестности точки М₀ интегралов от производных

Здесь Рассмотрим первый интеграл. Имеем

,

где – шар радиуса с центром в точке Перейдем в последнем интеграле к сферическим координатам, будем иметь

Чтобы выполнялось неравенство достаточно взять Свойство доказано.

4. В точках области D объемный потенциал удовлетворяет уравнению

Доказательство. Согласно определению функции Грина краевой задачи эллиптического типа и ее представления в виде

в 3D-случае,

в 2D-случае, где получим из формулы для потенциала

после применения оператора Лапласа:

5. Если D – конечная область и то при потенциал

§2. Потенциал двойного слоя

п.1. Пусть в точках Р₁ и Р₂ расположены заряды –e и +e. Направим вектор от отрицательного заряда к положительному:

Рис. 1.

Потенциал электростатического поля в точке М(x,y,z), созданного этими зарядами (диполем), имеет вид

или

где выражение , называют моментом диполя.

Далее запишем Устремим h 0 и считаем, что предел отношения существует. Тогда получим

(1)

где точка Р – это точка, к которой сближаются точки Р₁ и Р₂ при h 0.

Производная по направлению , как известно, имеет вид

В нашем случае

поэтому

г де – угол, отсчитываемый от к вектору против хода часовой стрелки:

Рис. 2.

Доказательство:

Отсюда следует:

.

Так как

а то справедливость формулы доказана.

В плоском случае

Итак, в трехмерном случае

( )

а в двухмерном

( )

Здесь вектор направлен от отрицательной "стороны" диполя к положительной.

Пусть поверхность S двухсторонняя с непрерывно меняющимся положением касательной плоскости к ней при переходе от одной точки поверхности к другой. Что значит, что поверхность односторонняя? Это значит, что если в некоторой точке выбрано положительное направление нормали , и точка движется по любому замкнутому контуру , причем направление вектора меняется непрерывно, то при возвращении в исходную точку она (нормаль) совпадает с начальным положением.

п.2. Пусть на поверхности S распределены диполи с плотностью .

Положительным направлением нормали к поверхности S назовем направление, совпадающее с направлением оси диполя – от знака минус к знаку плюс двух зарядов, образующих диполь.

Тогда потенциал поля в точке М пространства, создаваемый этими диполями, определяется как

(2)

и в плоском случае как .

И называется он потенциалом двойного слоя, см. рис. 3 и рис. 4.

Рис. 3. Два слоя зарядов, расположенных на расстоянии

И при получается двухсторонняя заряженная поверхность, рис. 4

Рис. 4. Двухсторонняя заряженная поверхность

Учитывая формулы ( ) и ( ), можем записать

(3)

в плоском случае.

Угол отсчитывается от вектора к вектору против хода часовой стрелки.

Обозначим через телесный угол, под которым из точки М виден элемент поверхности S, см. рис. 5.

Рис. 5.

Площадь куска сферы радиуса , высеченного конусом с вершиной в точке М и телесным углом , определяется выражением

И так как то потенциал примет вид

(4)

Здесь – телесный угол, под которым видна вся поверхность S.

Угол если угол острый, и если угол тупой, см. рис. 6 и рис. 7.

Рис. 6. Угол острый

Рис. 7. Угол тупой

Получается, что если вектор и точка М по одну сторону S, то угол острый. Это следует из того, что Если , то если , то

В дальнейшем положим, что – интегрируемые функции, а поверхность S кусочно-гладкая.

п.3. Свойства потенциала двойного слоя.

1) Потенциал двойного слоя определен всюду. Принимаем без доказательства.

2) В точках, не лежащих на несущей заряды поверхности S, – гармоническая функция.

Действительно. Воспользуемся формулой (2):

т. к.

Что и требовалось доказать.

3) Если поверхность S конечна, то при

Из формулы (3) имеем

где .

Отсюда следует справедливость свойства. Чтобы доказать следующее важное свойство 4, введем ряд вспомогательных понятий. Положим:

- S есть замкнутая поверхность;

- каждый луч, проведенный из любой точки, не принадлежащей поверхности S, пересекает ее конечное число k раз;

- в качестве положительного направления нормали к поверхности S выберем направление внутренней нормали.

Следовательно, если на поверхности S распределены диполи, отрицательно заряженной будет внешняя сторона поверхности, см. рис. 8.

Рис. 8.

Пусть плотность распределения диполей постоянна . В таком случае будем иметь потенциал вида:

Докажем. а) Пусть точка М вне S. В этом случае имеем конфигурацию:

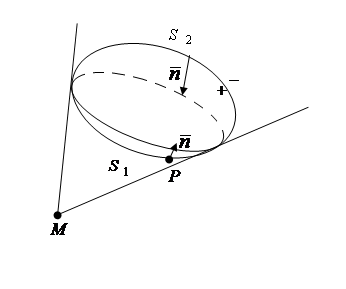
Рис. 9.

Телесным углом поверхность S разбивается на двеповерхности S₁ и S₂.

Очевидно, что

т. к. для S₁ и S₂ телесный угол по модулю одинаков, а знаки разные, из-за разнонаправленности векторов . Следовательно,

б) Пусть точка М на поверхности S. Будем иметь следующую конфигурацию.

S

Рис. 10.

Когда точка Р пробежит всю поверхность S, то сумма телесных углов составит полупространство, расположенное под касательной плоскостью в точке М. То есть Следовательно,

что и требовалось доказать.

в) Пусть точка М внутри поверхности S. И пусть (пока) всякий луч, проведенный из точки М, пересекает поверхность S один раз.

Тогда, очевидно

Пусть часть лучей (или все), проведенных из точки М, пересекает поверхность не более k раз, рис. 11.

Рис. 11.

Телесные углы, под которыми видны куски S₁ и S₃ будут положительны, а S₂ – отрицательны. В силу этого

Поэтому алгебраическая сумма всех телесных углов, над которыми видны все элементы поверхности S, будет опять равна Следовательно,

Сформулируем теперь свойство 4.

Если плотность моментов непрерывна на несущей поверхности S, то потенциал двойного слоя имеет разрыв первого рода (конечный скачок) в точках , равный

(5)

Здесь есть предел в точке М₀, когда точка , находясь внутри поверхности S.

И , когда точка М снаружи от S.

Пусть М₀ – рассматриваемая точка поверхности S, выбранная произвольно.

Рассмотрим вспомогательную функцию

(6)

Лемма. Функция непрерывна в точке М₀, т. е.

Доказательство. Пусть – некая - окрестность точки М₀, рис. 12.

М

М₀

Рис. 12.

Тогда поверхность , где . В таком случае

где

Функция непрерывна в точке М₀, потому что точка , и когда , то Следовательно, особенности нет.

Поэтому для величина как только

Далее имеем

Так как по предположению функция непрерывна в точке М₀, то

к огда достаточно мало. Знаменатель в форме взят для удобства, чтобы получилось , см. далее. Сделаем предположение, что луч, проведенный из точки М, пересекает поверхность не более раз, см. рис. 13. На рисунке 13 точки А и В суть следы пересечения области с поверхностью S.

Рис. 13.

Когда точка Р при интегрировании по пробегает от точки А до точки В, т. е. по поверхности , то

ибо

Отсюда следует

Если записать

то получится

как только . Что и требовалось доказать.

Докажем теперь свойство 4.

В выражении для потенциала двойного слоя точка М (точнее, ее координаты) является параметром несобственного интеграла. Перейдем в выражении (6) к пределу: .

Пусть изнутри (ВНТ) поверхности S. Имеем из формулы (6):

(а)

так как см. выше.

Пусть снаружи (НАР). Из формулы (6) получим

(б)

так как по выше доказанному.

Пусть на поверхности S. Из формулы (6) следует

. (в)

Так как в силу леммы функция непрерывна в точке М₀, то левые части у выражений (а), (б), (в) равны, т. е. .

Отсюда получаем цепочку равенств

из которой следует свойство 4, а именно:

Выпишем соотношения

(7)

(8)

(9)

В плоском случае потенциал двойного слоя имеет вид

.

Здесь – граница плоской области, см. рис. 14.

Рис. 14.

Аналогичные рассуждения в двухмерном случае приводят к формулам:

(10)

(11)

(12)

Эти формулы играют важную роль при сведении краевой дифференциальной задачи к интегральным уравнениям.

При численном решении краевой задачи решение интегральных уравнений предпочтительнее по многим причинам. Поэтому мы так подробно провели доказательство выше указанных свойств.