Вопрос 15.

При анализе ОЭС и ЕЭС возникает необходимость поиска экстр. нелинейной функции на множестве точек, удовлетворяющих нелинейным неравенствам.

Отсюда возникла теория экстремума в нелинейных задачах с ограничениями. Необходимое и достаточное условие существования такого экстремума было сформулировано Куном и Такером.

Теорема Куна-Такера

Если Ц(х)- целевая функция, g(х)- огр-я в форме неравенств, то для того, чтобы точка х была опт-й, т.е. Ц(х0)=min Ц(х) необходимо и достаточно, чтобы существовала точка , которую совместно с х , образовало бы седло функции Лагранжа.

Функция Лагранжа:

т.е. чтобы . Если L(х) и Ц(х) дифференциальные функции, то седловая точка может быть найдена из следующих условий:

Если ограничения записаны в форме равенств, в таком случае условия Кауна-Такера сводятся к применению метода множ-й Лагранжа

1 6 Применение методов возможных направлений для поиска экстремума целевой функции при решении задач оптимизации в электроэнергетике. Возможные направления. Градиент и антиградиент целевой функции. Способы задания длинны шага. Метод оптимизации при постоянной длине шага.

Методы возможных направлений.

Методы относятся к классу итеративных методов, в которых строится последовательность точек , стремящихся к абсолютному экстремуму целевой функции на основании критерия оптимизации, т.е. , лучше, чем .

С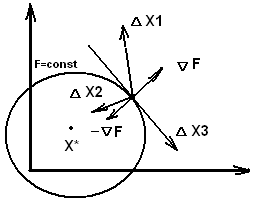 уть методов возможных направлений заключается в том, что спуск от начального приближения до абсолютного экстремума может осуществляться различными направлениями, называемыми возможными.

- рост целевой функции

- уменьшение

-

- возможные направления

Вектор, ортогональный к касательной функции, указывающий направление роста целевой функции называется градиентом целевой функции.

-градиент целевой функции

- - антиградиент является наилучшим из возможных направлений, указывающий путь наискорейшего убывания целевой функции.

Способы задания длины шага

,

где - длина шага вдоль вектора ;

- направление спуска на К-ом шаге.

Все методы нелинейного программирования, основанные на данном соотношении можно разделить на 2 класса по способу задания длины шага:

1. Класс основан на постоянной длине шага

Исходная длина шага задается примерно. Но при неудачно заданной длине шага может не выполняться критерий оптимизации, т.е.

16-1

нарушение критерия оптимизации, отсюда следует

,

,

.

Достоинством этих методов является малый объем вычислений на каждом шаге.

Недостатки – при неудачно заданных значениях длины шага q и , возможно большое количество шагов оптимизации, и следовательно, большой объем вычислений.

2. Класс - метод наискорейшего спуска

длина шага зависит от направления спуска и вычисляется из условия наискорейшего убывания целевой функции

Для того, чтобы найти оптимальное значение длины шага необходимо продифференцировать по длине шага и приравнять к нулю:

:

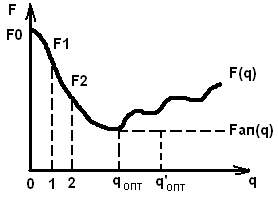- данная функция может быть нелинейной относительно q, и поэтому аппроксимируют полиномом 2-ой степени

псевдооптимальная длина шага

Найти

?