
- •Метод множителей Лагранжа
- •9 Размерность и физический смысл множителей Лагранжа в задачах оптимизации распределения нагрузки в энергосистеме.
- •10. Оптимальное распределение нагрузки при постоянном напоре гэс и структурная схема алгоритма поиска данного распределения.
- •11.Оптимальное распределение нагрузки при переменном напоре гэс.
- •12.Оптимальное распределение нагрузки между агрегатами эл/ст.
- •Вопрос 15.
- •1 7. Применение метода наискорейшего спуска при решении задач оптимизации в электроэнергетике.
- •1 8.Способ вычисления оптимальной длины шага вдоль заданного направления спуска при решении задач оптимизации в электроэнергетике.
- •19 Применение метода покоординатной оптимизации в электроэнергетике. Внешний и внутренний циклы метода.
- •2 0. Применение градиентных методов оптимизации в электроэнергетике. Критерии сходимости. Градиентный метод в сочетании с методом наискорейшего спуска.
- •22 Учет гораничений в форме равенств при решении задач оптимизации в электроэнергетике. Приведенный градиент
- •23. Учет ограничений в форме неравенств
П онятие
оптимизации. Основные задачи оптимизации
в электроэнергетике. Степени свободы
электроэнергетической системы. Допустимый
и оптимальный режимы.
онятие
оптимизации. Основные задачи оптимизации
в электроэнергетике. Степени свободы
электроэнергетической системы. Допустимый
и оптимальный режимы.
Оптимальным называется процесс или объект, который лучше других в соответствии с некоторым критерием оптимальности. Сравнение процессов – задача, решение которой показывает, на сколько один процесс лучше другого в соответствии с неким критерием оптимальности.
Критерий оптимальности:
- количественный (снижение расхода условного топлива на ТЭС);
- качественный (улучшение влияния электроэнергетического объекта на экологию).
Задачи оптимизации в электроэнергетике:
1. Стратегия развития энергосистемы (сооружение, реконструкция электроэнергетических объектов, местоположение, мощность и срок ввода в эксплуатацию новых электростанций, подстанций, ЛЭП );
2. Выбор оптимальной конфигурации эл.сетей, соединяющих подсистемы или распределяющих передающих энергию внутри сети;
3. Оптимальное распределение нагрузки между электростанциями;
4. Оптимальная стратегия использования материальных ресурсов;
5. Выбор оптимальных маршрутов грузоперевозки, в т.ч. перевозки топлива;
6.Выбор точек размыкания линии с двухсторонним питанием;
7. Выбор маршрута осмотра электротехнических объектов.
Взаимосвязь
расчета установившегося режима и его
оптимизации.
![]()
Параметры
уравнения установившегося режима
![]() :
:
-
![]() -
независимые, заданные параметры;
-
независимые, заданные параметры;
-
![]() -
зависимые параметры.
-
зависимые параметры.
Уравнения установившегося режима связывают между собой его параметры.
Пусть k – число уравнений, n – число неизвестных. Если k=n, то система полностью определена. При k<n система недоопределена. Избыток числа неизвестных над числом уравнений физически означает что система имеет (n-k) степеней свободы.

У УР
БМ
УР
БМ
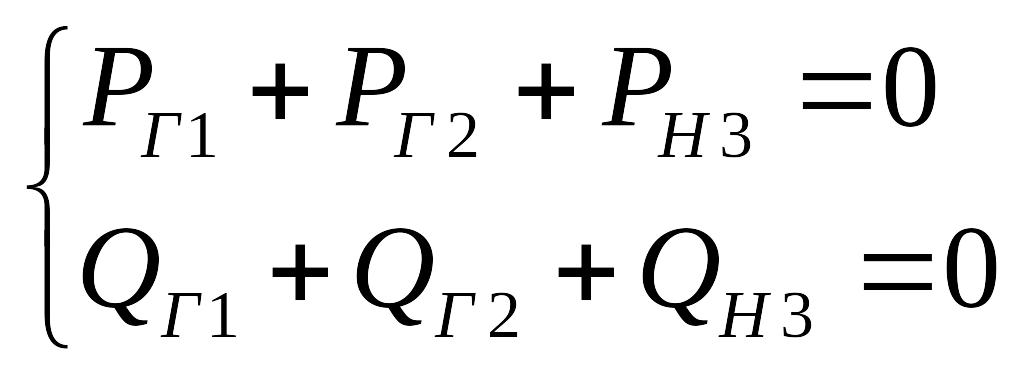
![]() -
заданы
-
заданы
Система
имеет 2 степени свободы
![]() 2 любых параметра могут быть заданы в
пределах минимальных и максимальных
допустимых значений.
2 любых параметра могут быть заданы в
пределах минимальных и максимальных
допустимых значений.
Регулируются P и Q:
- с помощью регулирующих трансформаторов;
- при включении/отключении оборудования.
Из всех возможных состояний системы наибольший интерес представляют допустимые режимы, в которых значения параметров установившегося режима находятся в заданных пределах.
Задача оптимизации: найти наиболее экономичный режим.
Рост числа степеней свободы – рост возможности оптимизации и усложнение задач.
|
|
генератор |
нагрузка |
Z |
X |
Q, |
U, |
Y |
P,U |
P,Q |
В задаче оптимизации используются добавочные степени свободы для изменения переменных параметров режима, чтобы из множества состояний системы выбрать такое, которое обеспечит минимальный суммарный расход условного топлива, что снижает экономические затраты.
70% электроэнергии вырабатывается на ТЭЦ:
- 40% при сжигании газа;
- 10% при сжигании мазута;
- 20% при сжигании угля.
При оптимизации режима за счет наличия степеней свободы выбираются параметры режима, обеспечивающие минимальные суммарные потери активной мощности.
Применение метода множителей Лагранжа при решении задач оптимизации в электроэнергетике.
М етод
позволяет отыскать условные или
относительные экстремумы функции,
которые являются ее минимумом или
максимумом при выполнении дополнительных
условий в форме равенств, т.е. уравнений
связи.
етод
позволяет отыскать условные или
относительные экстремумы функции,
которые являются ее минимумом или
максимумом при выполнении дополнительных
условий в форме равенств, т.е. уравнений
связи.
Данный
метод дает возможность найти систему
уравнений, которой удовлетворял экстремум
функции
![]() на множестве N.
Для того чтобы найти экстремум,
характеризующийся на множестве N
вектором
на множестве N.
Для того чтобы найти экстремум,
характеризующийся на множестве N
вектором
![]() необходимо найти m
чисел
необходимо найти m
чисел
![]() ,
которые совместно с вектором
,
которые совместно с вектором
![]() удовлетворяют
удовлетворяют
![]() уравнениям с
неизвестными.
уравнениям с
неизвестными.
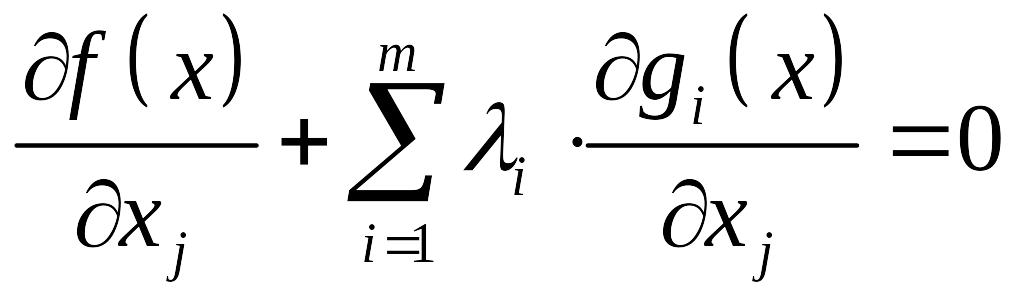
Эти уравнения получены как условный экстремум функции Лагранжа.
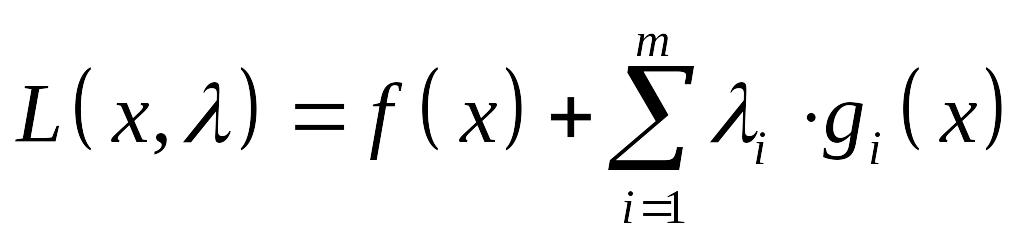
Структура энергосистемы
![]()
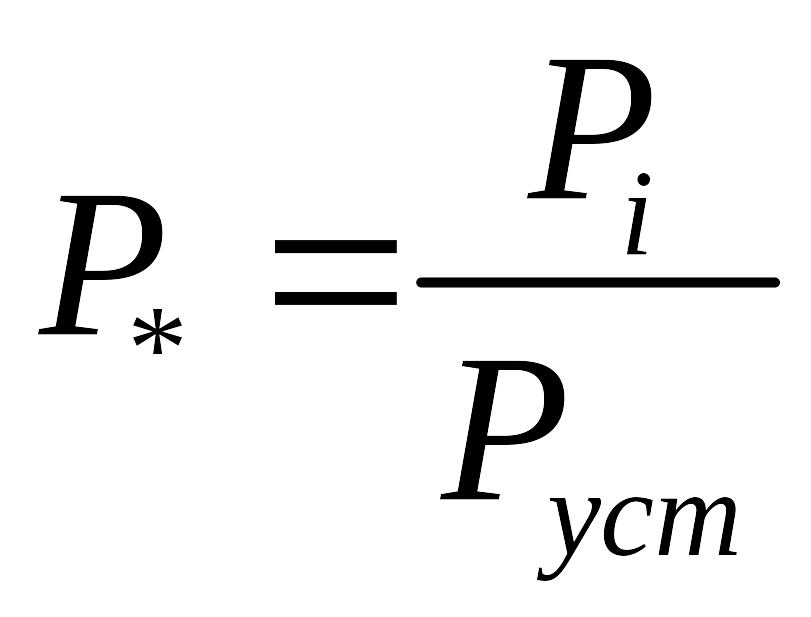
![]() (РФ,1996)
(РФ,1996)
Цена (АЭС) > Цена (КЭС) > Цена (ГЭС)
tпуск=часы tпуск=1 мин
ТЭС – тепловая система;
ТЭС+ГЭС – гидротепловая (смешанная) система.
Параметры энергосистемы:
- технологические:
а) ГЭС (расход пара, напор);
б) ТЭС (расход пара, расход охлаждающей воды);
-
электромеханические (![]() ).
).
Т епловая
и гидротепловая системы. Структура
энергосистемы и декомпозиция задачи
наивыгоднейшего распределения нагрузки
в энергосистеме. Иерархия данной задачи
в пространстве, времени и ситуации.
епловая
и гидротепловая системы. Структура
энергосистемы и декомпозиция задачи
наивыгоднейшего распределения нагрузки
в энергосистеме. Иерархия данной задачи
в пространстве, времени и ситуации.
Руст- установившееся активная мощность.
Руст=РГЭС+РГАЭС+РКЭС+РТЭЦ+РГТУ+РПГУ+РАЭС+Рпр.
Р*=Рi / РУСТ.
Так Р*ГЭС=0,14; Р*КЭС=0,46; Р*ТЭЦ=0,24; Р*АЭС=0,16.
Цена (АЭС)> Цена (КЭС)> Цена (ТЭС).
Тепловая система: ТЭС.
А если ТЭС+ГЭС, то получиться гидротепловая система.
Параметры: 1-технологические;
2-электротехнические.
Технологические деляться на:
-Расходы напора на ГЭС;
-Расходы пара на ТЭС.
Электротехнические: Uy, IB, P, Q, KTP.
Одной из главных задач управления ЭС в условиях нормальной эксплуатации является задача наивыгоднейшего распределения нагрузки между генераторами, что обеспечивает высокую эффективность использования трудовых, материальных и экономических ресурсов.
Данная задача имеет декомпозицию (разделение) в пространстве, времени и ситуации.
А). Уровни в разделение по пространству:
1.Распределение нагрузки между ОЭС и ЕЭС;
2.Распределение нагрузки между РЭС и ОЭС;
3.Распределение нагрузки между ЭС и РЭС;
4.Распределение нагрузки между агрегатами ЭС.
Б). Разделение по времени:
1.Долгосрочное планирование (мес.,год)- определение прогнозируемых графиков нагрузки, необходимых для проведения технологических и хозяйственных мероприятий.
2.Краткосрочное планирование (мес.,сут.)- определение плановой нагрузки ЭС.
3.Регулирование мощности в ЭС в темпе производств, протекающих в ЭЭС.
В). Разделение по ситуации:
1.Нормальный режим.
2.Аварийный режим.
3.Послеаварийный режим.
Определение оптимального распределения нагрузки между ТЭС методом множителей Лагранжа. Относительные приросты ТЭС.

Пусть имеется ЭС с числом n ТЭС, для которых заданы расходные характеристики Bi (Pi ) (на i-ой ТЭС) суммарная нагрузка Р.
Задачу навыгоднейшего распределения нагрузки рассмотрим при помощи метода Лагранжа:
Уравнение цели:
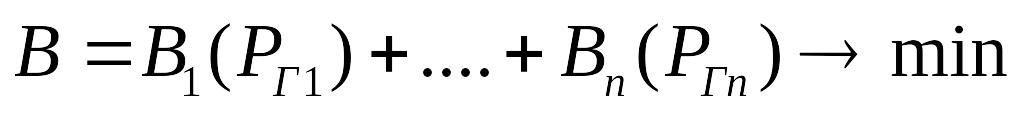
где В- суммарный расход топлива.
Уравнение связи:
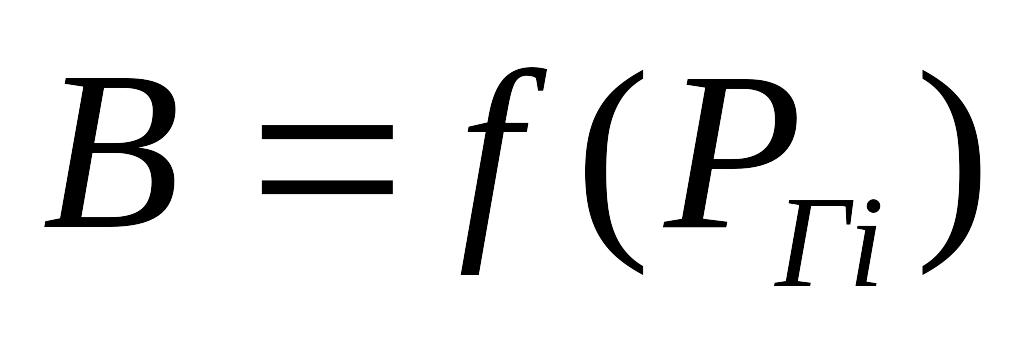
Уравнение ограничений:
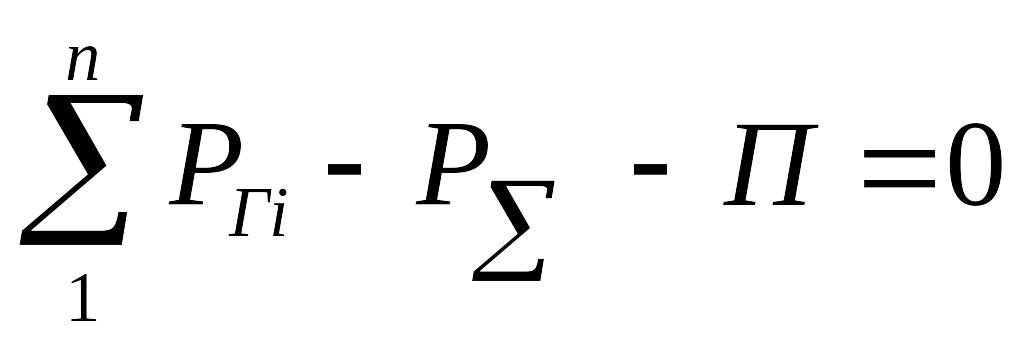
где Р-суммарная нагрузка.
П- потери.
Функция Лагранжа:
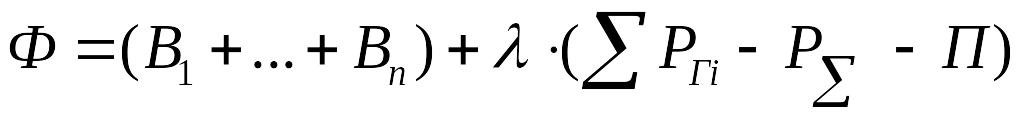 .
.
Дифференцируя функцию Лагранжа по РГ1….PГn и приравняв все производные к нулю, получим:
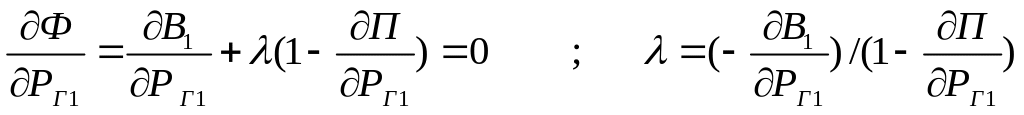

………….…………………………………………………
………….………………………………………………….
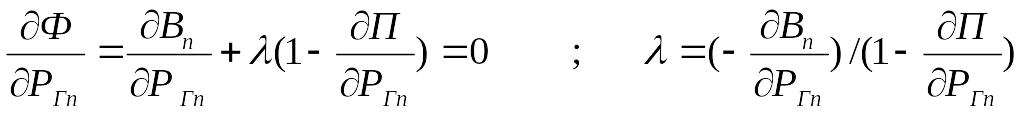
Таким образом, условия оптимизации:
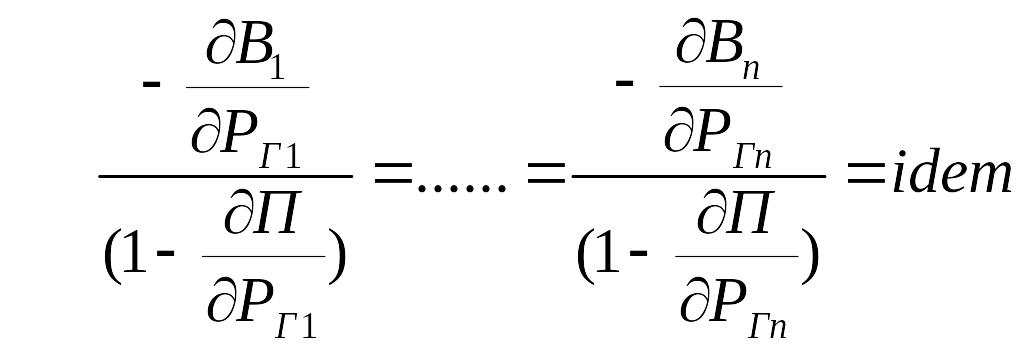
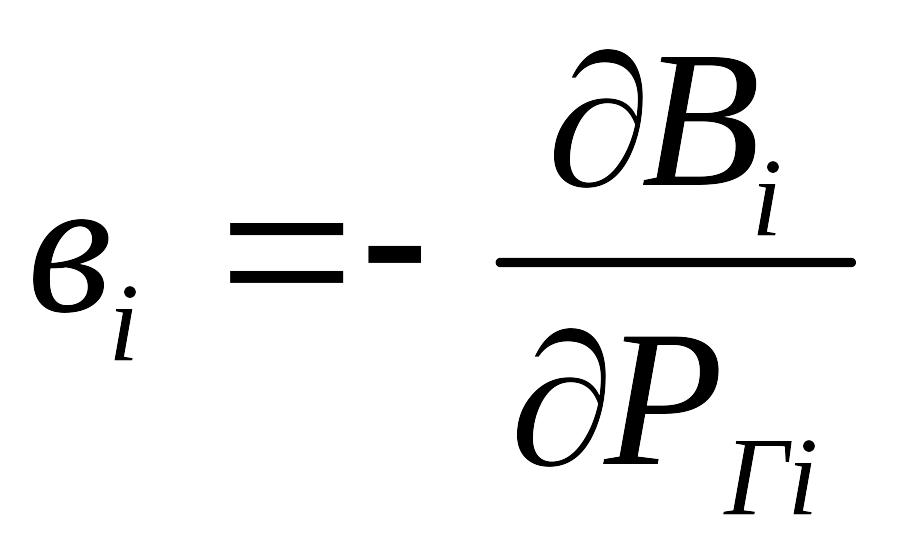 ---относительный
прирост расхода топлива (на сколько
изменится расход топлива, если мощность
i-ой
станции измениться на Рi
).
---относительный
прирост расхода топлива (на сколько
изменится расход топлива, если мощность
i-ой
станции измениться на Рi
).
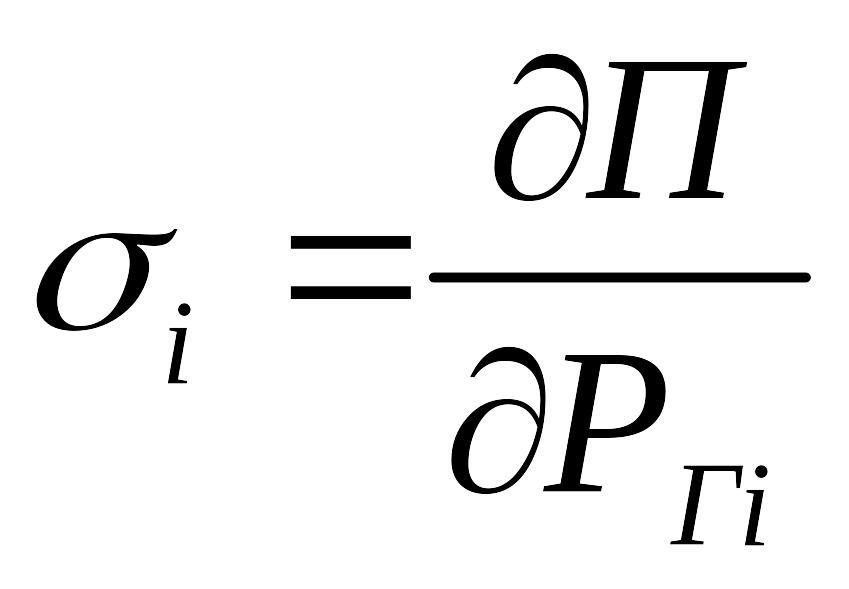
 ---относительный
прирост потерь активной мощности ( на
сколько изменяться потери активной
мощности, если мощность i-ой
станции измениться на Рi
)
---относительный
прирост потерь активной мощности ( на
сколько изменяться потери активной
мощности, если мощность i-ой
станции измениться на Рi
)
Условие оптимальности распределения нагрузки:
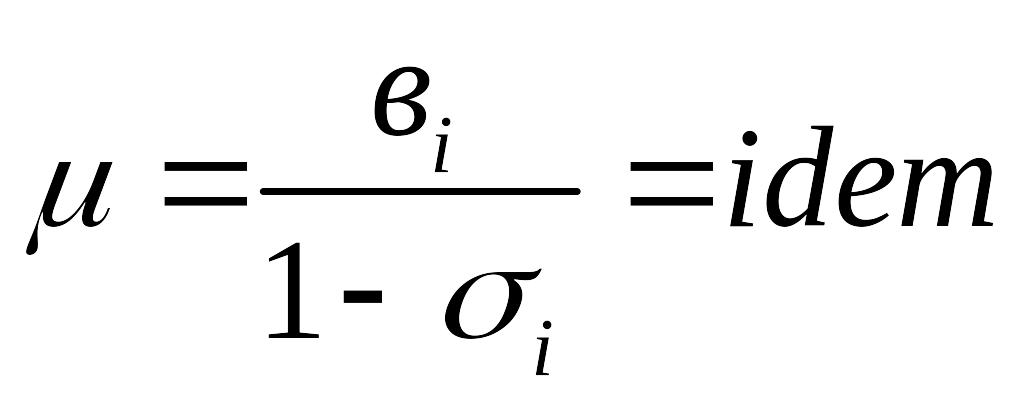
Если
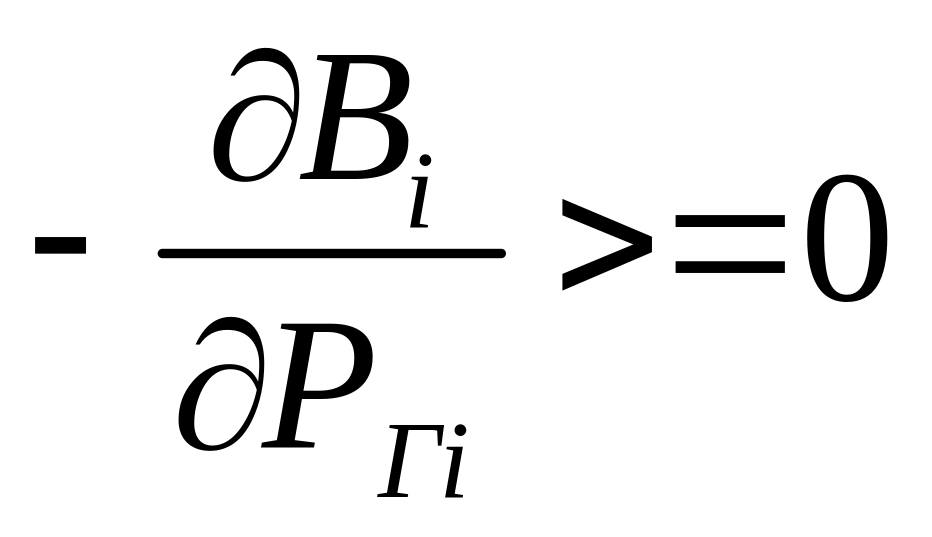 и выполняется условие оптимальности,
то функции соответствует min,
иначе max.
и выполняется условие оптимальности,
то функции соответствует min,
иначе max.
Физический смысл условия оптимальности:
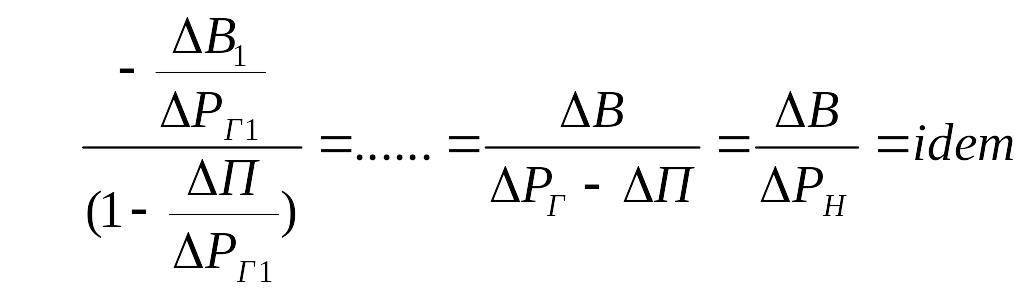
![]() --мощность
доведенная до потребителя.
--мощность
доведенная до потребителя.
Если
 ,
то на какой либо эл. станции наблюдается
чрезмерный расход топлива, т.е. не
рациональное распределение нагрузки,
не экономично.
,
то на какой либо эл. станции наблюдается
чрезмерный расход топлива, т.е. не
рациональное распределение нагрузки,
не экономично.
О пределение
оптимального распределения нагрузки
между ТЭС методом множителей Лагранжа.
Структурная схема алгоритма.
пределение
оптимального распределения нагрузки
между ТЭС методом множителей Лагранжа.
Структурная схема алгоритма.
Пусть имеется ЭС с числом n ТЭС, для которых заданы расходные характеристики Bi (Pi ) (на i-ой ТЭС) суммарная нагрузка Р.
Задачу навыгоднейшего распределения нагрузки рассмотрим при помощи метода Лагранжа:
Уравнение цели:
где В- суммарный расход топлива.
Уравнение связи:
Уравнение ограничений:
где Р-суммарная нагрузка.
П- потери.
Функция Лагранжа: .
Дифференцируя функцию Лагранжа по РГ1….PГn и приравняв все производные к нулю, получим:
………….…………………………………………………
………….………………………………………………….
Таким образом, условия оптимизации:
 ---относительный
прирост расхода топлива (на сколько
измениться расход топлива, если мощность
i-ой
станции измениться на Рi
).
---относительный
прирост расхода топлива (на сколько
измениться расход топлива, если мощность
i-ой
станции измениться на Рi
).
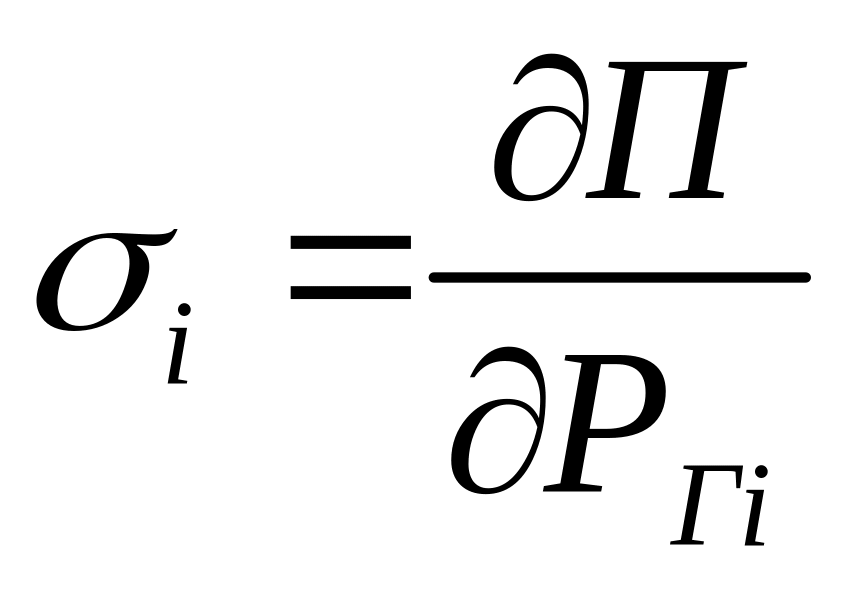 ---относительный
прирост потерь активной мощности ( на
сколько изменяться потери активной
мощности, если мощность i-ой
станции измениться на Рi
)
---относительный
прирост потерь активной мощности ( на
сколько изменяться потери активной
мощности, если мощность i-ой
станции измениться на Рi
)
У словие
оптимальности распределения нагрузки:
словие
оптимальности распределения нагрузки:
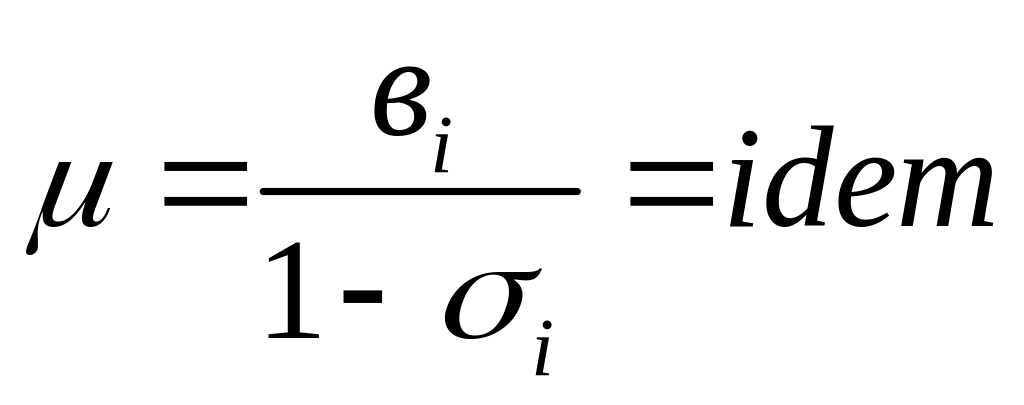
Если и выполняется условие оптимальности, то функции соответствует min, иначе max.
Физический смысл условия оптимальности:
--мощность доведенная до потребителя.
Если , то на какой либо эл. станции наблюдается чрезмерный расход топлива, т.е. не рациональное распределение нагрузки, не экономично.
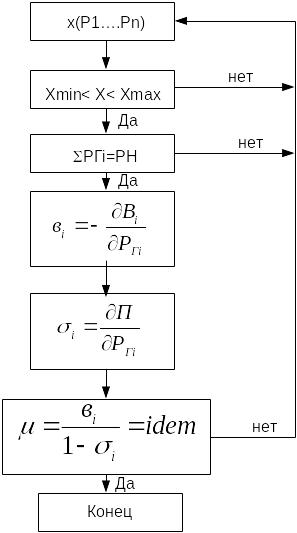
Алгоритм
Н аивыгоднейшее
распределение нагрузки между ТЭС без
учета потерь активной мощности. Физический
смысл равенства относительных приростов.
аивыгоднейшее
распределение нагрузки между ТЭС без
учета потерь активной мощности. Физический
смысл равенства относительных приростов.
Это случай задачи наивыгоднейшего распределения нагрузки между агрегатами электростанций или в ЭС с высокой концентрацией мощности.
![]()
![]()
![]() -усл-ие
оптимальности, т.е. оно соотв-ет рав-ву
отн-ых приростов
-усл-ие
оптимальности, т.е. оно соотв-ет рав-ву
отн-ых приростов
Р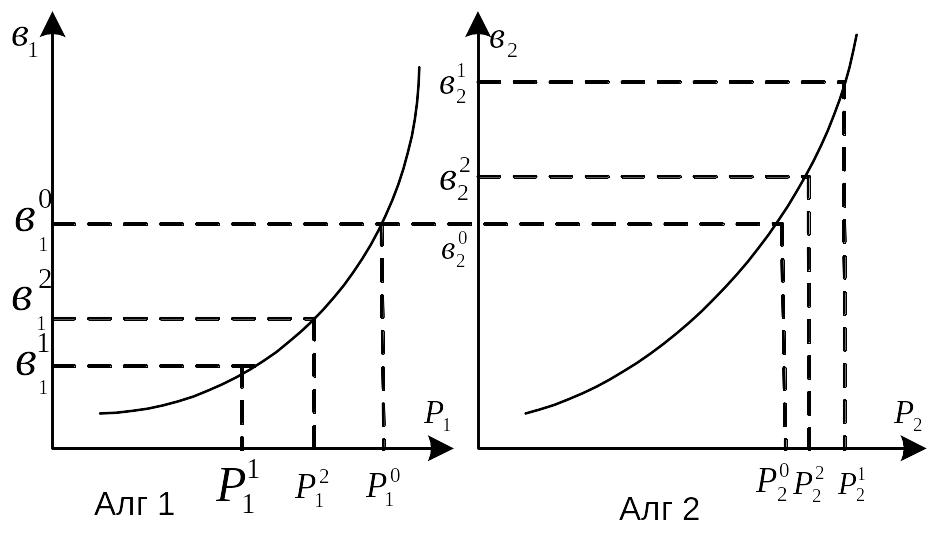 ассмотрим
на примере из 2-х агрегатов Эл/ст
ассмотрим
на примере из 2-х агрегатов Эл/ст
Если
у двух агрегатов имещих мощн-ь
![]() и
и
![]() и возрастные хар-ки
и возрастные хар-ки
![]() и отн-ные приросты, не равные друг другу
(
и отн-ные приросты, не равные друг другу
(![]() ).
).
Догрузим
агрегат 1 на некоторое значение
![]() ,
а агрегат 2 –разгрузим наэто же
,
а агрегат 2 –разгрузим наэто же
Когда
![]() ,
дальнейшее перераспределение нагрузки
не принесёт экономии
мы имеет наив-шее распр- ие нагр-и –
оптим. режим.
,
дальнейшее перераспределение нагрузки
не принесёт экономии
мы имеет наив-шее распр- ие нагр-и –
оптим. режим.
Алгоримт оптим-ции с испол-ем ЭВМ.
![]()
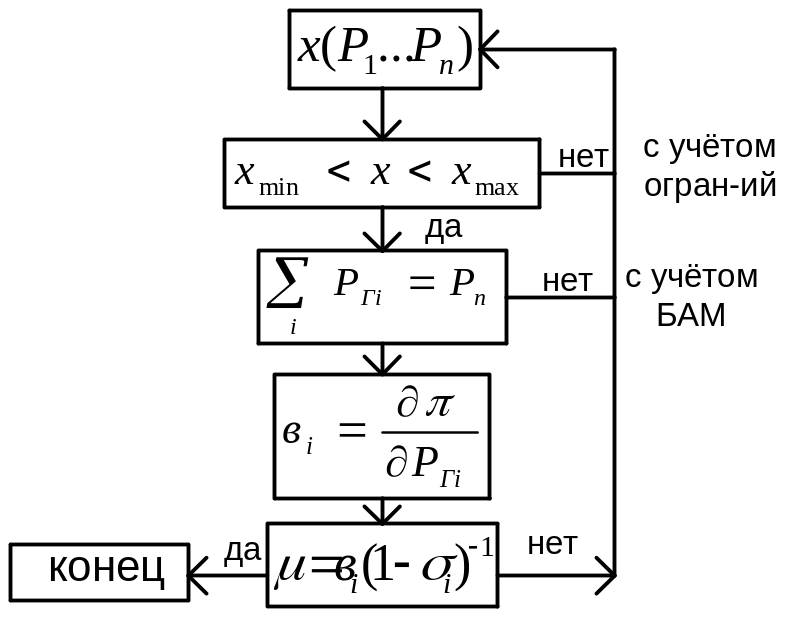 -
берётся произ-ое распт- ие нагр-ки м/у
эл/ст
-
берётся произ-ое распт- ие нагр-ки м/у
эл/ст
Определение оптимального распределение нагрузки в энергосистеме с ГЭС и ТЭС методом множителей Лагранжа. Относительные приросты ТЭС и ГЭС.
З -ча
наив-шего распределения нагр-и в
гидротепл. Системе делится на:
-ча
наив-шего распределения нагр-и в
гидротепл. Системе делится на:
1 З-ча оптим-ции длит-ных реж-ов; 2 З-ча оптим-ции краткосрочн. режим (сутки и менее).
Для всего цикла регул- ия ГЭС находит наив-шее распр-е нагрузки м/у всеми станциями сист-ы, и опр-ет оптим режим исп-ния гидроресурсов, т.е. график сработки и заполнения водохранилищадля всей ГЭС с-мы. На основании этих расчётов регламентируются гидроресурсы на более короткий период оптим-ции.
Метод множителей Лагранжа
1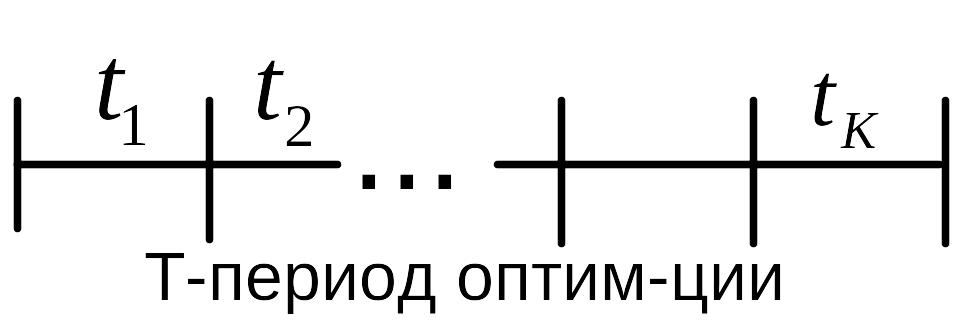 Ур-ние цели
Ур-ние цели ![]()
![]() -
расход топлива эквив-ой ТЭС за период
времени Т
-
расход топлива эквив-ой ТЭС за период
времени Т
![]()
2 Ур-ние связи
2.1
![]() -
расх-ая хар-ка ТЭС
-
расх-ая хар-ка ТЭС
2.2
![]() -
расх хар-ка ГЭС
-
расх хар-ка ГЭС
3 Ур-ние огр-ний
![]() -ур-ний:
-ур-ний:
![]()
![]() -
сумма нагр-ки,
-
сумма нагр-ки,
![]() -
сумма потерь.
-
сумма потерь.
![]() ур-ние:
ур-ние:
![]()
![]() -
заданные огр-ния по стоку для j-ой
ГЭС,
-
заданные огр-ния по стоку для j-ой
ГЭС,
![]() -
расход, с которым работала ГЭС в период
Т
-
расход, с которым работала ГЭС в период
Т
![]() -
мощн-ти
-
мощн-ти
![]() -ой
ГЭС на инт t
-ой
ГЭС на инт t
4 Ф-ция Лагранжа
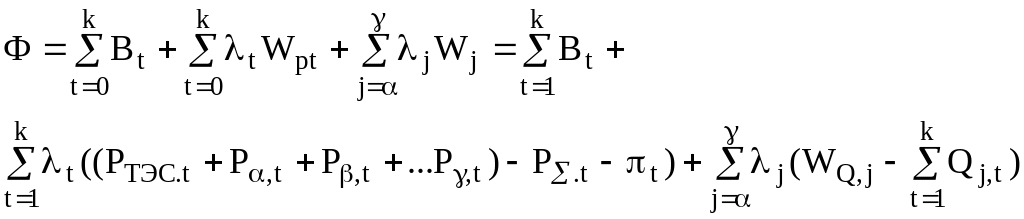
Кол-во
неиз-ых
![]()
![]()
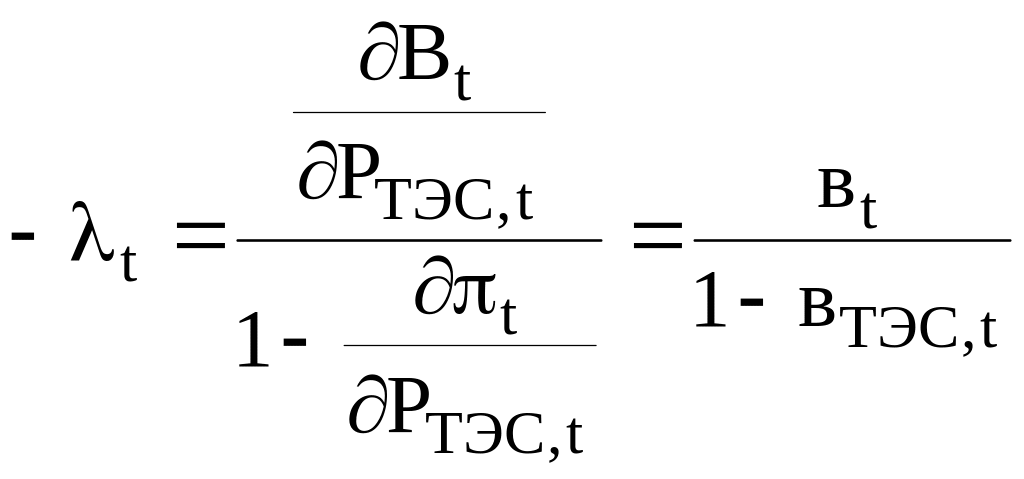

![]() ур-ний:
ур-ний:
![]() ;
….
;
….![]()
![]()
![]() ,
где
,
где
![]() ,
,
![]()
ур-ний:
![]() (*)
(*)
Все величины, вход-щие в сист-у ур-ний (*) опр-ся энерг-ми хар-ми оборуд-ния, т.е. отн-ный прирост расх топлива (В) и расх топлива на ТЭС (q), или же парам-ми сети.
Индексы при этих велич-ах можно опус-ть
![]()
![]() -
усл оптим-ции режима гидро-теплов с-мы.
-
усл оптим-ции режима гидро-теплов с-мы.
Смысл усл-ия оптим-ции
В
том, что для наив-шего распр-ия нагрузки
необх-мо в теч всего периода оптим-ции
собл-ть пост-ное соотн-ние
![]() м/у ТЭС и каж-ой из ГЭС, т.е. м/у ТЭС и
м/у ТЭС и каж-ой из ГЭС, т.е. м/у ТЭС и
![]() -ГЭС
нагрузка должна рапр-ся по соотн-ию
-ГЭС
нагрузка должна рапр-ся по соотн-ию
![]() и
это постоянное соотн-ие должно собл-ся
в теч. всех периодов оптим-ции
и
это постоянное соотн-ие должно собл-ся
в теч. всех периодов оптим-ции
Соотн-ие
м/у ТЭС и
![]() -ГЭС
-ГЭС
![]()
При
усл-вии соблюдения баланса величины
![]() ,
,
![]() связывают м/у собой режимы ТЭС и соотв-щей
ГЭС.
связывают м/у собой режимы ТЭС и соотв-щей
ГЭС.
9 Размерность и физический смысл множителей Лагранжа в задачах оптимизации распределения нагрузки в энергосистеме.
Размерность и физический смысл множителей Лагранжа
1 ТЭС и 1 ГЭС
![]() если
пренебречь потерями
если
пренебречь потерями
![]() ,
то усл-вие оптим-ции
,
то усл-вие оптим-ции
![]()
![]() ;
;
![]()
![]()
![]()
![]()
![]() -
мера эффект-ти использ-я гидроресурсов,
т.е. ккая экономия топлива будет получена
на ТЭС при измен-ии расхода на ГЭС на
-
мера эффект-ти использ-я гидроресурсов,
т.е. ккая экономия топлива будет получена
на ТЭС при измен-ии расхода на ГЭС на
![]() .
.
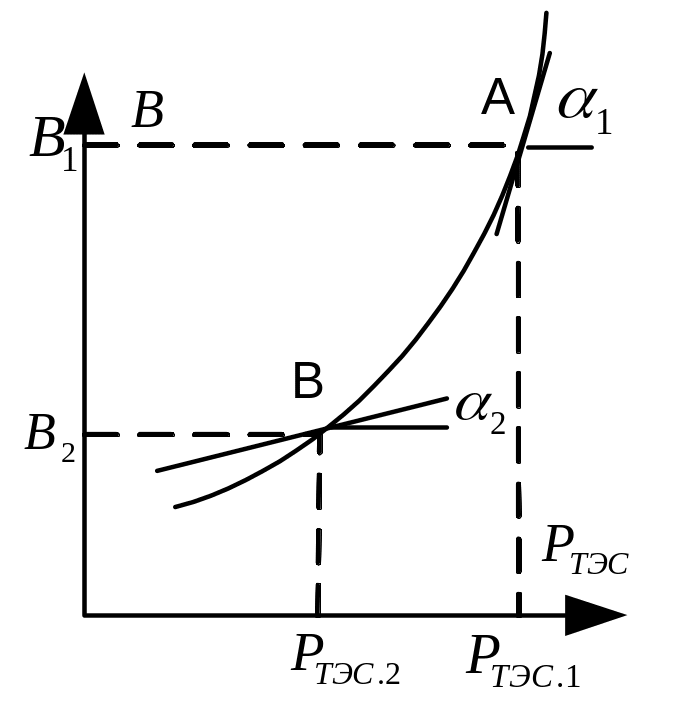
Наивыгодн-ший
режим тот, при к-ом эфф-сть исп-ния
ресурсов на к-ой ГЭС одинакова на всём
периде оптим-ции, т.е.
![]()
![]()
![]()
 ;
;
![]() ;
;
![]()
![]()
 ;
;
![]()
![]()
![]()
![]() ,
,
![]()
Эффект-ть использ-я гидроресурсов в данной с-ме (т.е. в с-ме с недозагруженной ГЭС) пропорц-на расходу на ГЭС.
Если ГЭС работает с малым расходом, то в с-ме имеется неэкон-но работающая ТЭС.
10. Оптимальное распределение нагрузки при постоянном напоре гэс и структурная схема алгоритма поиска данного распределения.
Д ля
всего цикла регулирования распределения
ГЭС находится наивыгоднейшее распределение
нагрузки между всеми станциями системы,
и опред-ся оптимальный режим использования
гидроресурсов, т.е. график сработки и
заполнения водохранилища для всех ГЭС
системы. На основании этих расчетов
регламентируются гидроресурсы на более
короткий период оптимизации.
ля
всего цикла регулирования распределения
ГЭС находится наивыгоднейшее распределение
нагрузки между всеми станциями системы,
и опред-ся оптимальный режим использования
гидроресурсов, т.е. график сработки и
заполнения водохранилища для всех ГЭС
системы. На основании этих расчетов
регламентируются гидроресурсы на более
короткий период оптимизации.
В течении всего промежутка напор не меняется, т.е. Е /3Н2О= const
W = QH ; Q- расход; Н- напор; - кпд.
W=(dV/dT)g(hВБ – hНБ )
j=, , ……ГЭС
Любая ГЭС за период оптимизации Т может израсходовать определенное количество гидроресурса WQj.
Структурная схема алгоритма распред-я нагр. при пост. напоре.
Для наивыгоднейшего распределения нагрузки необходимо в процессе расчета подобрать в соответствии с заданными ограничениями стока на ГЭС и найти такое распределение нагрузки, при котором в течение всего периода оптимизации не меняется = idem. Неопред-ть обусл-ет необходимость применения итерационного решения.
Исходные данные
1) Р1, Р2 ..РК t1 …tК – нагрузки
2) Расходные характеристики В(РТЭС ), Q(PТЭС )
3) Характеристики относительных приростов q(PГЭС ), b(PТЭС)
4) Ограничение по стоку и по мощностям станций W задан ГЭС
РТЭС max; РТЭС min; РГЭС max; РГЭС min.
Исходн. Данные 1 Зад-ся нагрузки РГЭС1 для t =1
t
 = 1……..k
РГЭС
= РГЭС t
p
= 1……..k
РГЭС
= РГЭС t
p
Р



 ГЭС
min
РГЭС1
РГЭС
max
нет
ГЭС
min
РГЭС1
РГЭС
max
нет
РТЭС = Рt – РГЭС
Р
 ТЭС
min
РТЭС
РТЭС
max
нет
ТЭС
min
РТЭС
РТЭС
max
нетОпределение ГЭС, ТЭС
b*= b/(1-b ТЭС )
q*= q/(1-q ГЭС )
t
=ср - t

=
0
=
0Рассчит. Wк
W
 ГЭС
=
Wt
= Wзад
нет
ГЭС
=
Wt
= Wзад
нет
конец
Для кажд. интервала t определ-ся коэф-т t. Поскольку распред-е нагрузки было произвольным t idem, т.е. режим неоптимальный и выравнив-е производ-ся по отношению к среднему значению.
