1 0.2 Размерность и физический смысл множителей Лагранжа в задачах оптимизации распределения нагрузки в энергосистеме

экономию топлива за счет раз­грузки неэкономичного оборудования. Если же ГЭС работает с большими расходами и мощностью, то на тепловых станциях используется более экономичное обо­рудование, а следовательно, происходит уменьшение λ.

В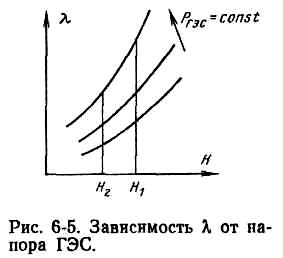 данной задаче заданы ограничения стока ГЭС. Коэффициент λ должен соответствовать заданному стоку (рис. 6-4). Эта задача решается подбором.

Коэффициент λ прямо пропорционально связан с на­пором ГЭС. Действительно, если ГЭС работает с по­стоянной мощностью , а напоры ее Н₁ и Н₂ раз­личны, то при Н₁ > Н₂ Q₁ < Q₂ (рис. 6.5).

11.1 Опт. Распред-ие нагрузки при постоянном напоре гэс и структурная схема алгоритма поиска данного распределения

Пусть в системе имеется одна эквивалентная ТЭС и j ГЭС. Каждая ГЭС за период Т может израсходовать опред. кол-во энергоресурса. Задача – полу­чить наивыгоднейшее распределение нагрузки между станциями.

1. Уравнение цели: .

Расход топлива эквивалентной ТЭС Bt зависит от того, с какой мощностью она будет работать в каждом интервале времени t = l, 2, ..., k.

2. Уравнения связи – расходная энергетическая хар-ка эквивалентной ТЭС В(Ртэс) и расход­ные энергетические хар-ки каждой ГЭС Qj(Pj, Hj).

3. Уравнения ограничений. Для каждого интервала имеется балансо­вое уравнение мощностей: . Для каждой ГЭС задается ограничение по стоку: , где P_t = P_l, P₂ ... - нагрузка си­стемы в интервале t = 1, 2, ..., k; Р_ТЭС,t - мощность ТЭС; - мощности ГЭС; – потери P; - заданные ог­раничения стока; - расход ГЭС в каждом интервале дли­тельностью .

4. Уравнение оптимизации: , где – относит. прирост расхода топлива ТЭС; – относит, прирост расхода воды j-й ГЭС; , – относит, приросты потерь P при изменении мощностей ТЭС и ГЭС.

Функция Лагранжа: .

Неизвестными величинами будут мощности ТЭС и каждой j-й ГЭС в каждом t-м интервале вре­мени. Неизвестны также множители Лагранжа: и . Общее число неизвестных jt+2t+j. Чтобы решить задачу, необходимо составить jt+2t+j уравнений. Если дифференцировать ф-ю Лагранжа по независ. переменным, получим jt+t ур-ий. Частные производные от ф-и Лагранжа берутся по мощно­стям

При решении этих ур-ий м. определить jt+t неизвестных. Балансовые ур-ия стока дают j ур-ий, а балансовые ур-ия мощности — t ур-ий. Т. о, число ур-ий достаточно для опре­деления неизвестных.

11.2 Опт. Распред-ие нагрузки при постоянном напоре гэс и структурная схема алгоритма поиска данного распределения

Производные по мощности ТЭС имеют вид:

(*)

Производные по мощности ГЭС дают уравнения: Отсюда получим:

Из этой системы и уравнений (*) получаем условия опти­мизации:

И ндексы времени м. опустить и получим окончательный вид уравнения оптими­зации:

Это условие означает, что для наивы­годнейшего распред-ия нагрузки необходимо для все­го периода оптимизации соблюдать постоянное соотно­шение между ТЭС и ГЭС. Между ТЭС и ГЭС α нагрузка должна распределяйся по соотношению Аналогично для ГЭС β. Одновременно требуется выполнить . Величины связывают режим ТЭС и соот­ветствующей ГЭС. ГЭС могут различаться своим напором и расходом, поэтому для каждой ГЭС имеется свой .

Блоки 1—3. Задается нагрузка ГЭС Р_ГЭС,1 для t = l и про­веряется ее допустимость. Если мощности ГЭС не удовлетворяют ограничениям, то они корректируются с приращением ± ΔP.

Блоки 4 и 5. Из уравнения баланса определяется мощность ТЭС и проверяется ее допустимость. Если она недопустима, то кор­ректируется мощность ГЭС и расчет возвращается в 2.