4.1 Применение метода множителей Лагранжа для оптимизации перетоков мощности в электрической сети

Применение метода Лагранжа для решения задачи оп­тимального распределения потоков мощности в сети состоит в определении минимума функции Лагранжа, в которую входят потери активной мощности

и уравнения пер­вого закона Кирхгофа (1):

;

; каждое из которых умножа­ется на соответствующий множитель Лагранжа. Рассмот­рим задачу оптимизации режима сети на рис. 13.2, когда потоки реактивной мощности в линиях Q_kj равны нулю.

Равенство нулю потоков Q в линиях 12, 23, 31 означает, что в узлах 2 и 3 на рис. 13.2 имеет место полная компен­сация реактивной мощности. Необходимо определить (2)

при выполнении двух ограничений равенств из (1)

. (3)

Функция Лагранжа

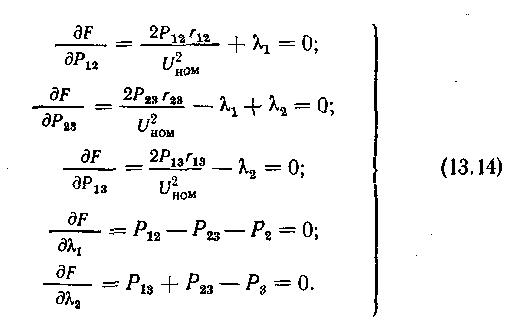, где и - множители Лагранжа.

З

(4)

адача на условный экстремум (2), (3) с тремя переменными P₁₂, Р₂₃ и Р₁₃ сведена к определению безуслов­ного экстремума (минимума) функции Лагранжа, которая зависит от пяти переменных; трех потоков мощно­сти и двух

4.2 Применение метода множителей Лагранжа для оптимизации перетоков мощности в электрической сети

множителей Лагранжа и . Минимум функ­ции Лагранжа соответствует решению исходной задачи и определяется равенством нулю пяти частных производ­ных:

Для решения системы линейных алгебраических урав­нений (4) преобразуем ее первые три уравнения в урав­нение второго закона Кирхгофа, исключив из них множи­тели Лагранжа. В результате получим выражение:

.

Решая два последних уравнения системы (4) совместно с этим уравнением, получим

.

Отсюда .

5.1 Оптимизация распределения перетоков мощности сложной электрической сети

Оптимизация распределения мощностей в сложной сети при выполнении первого закона Кирхгофа приводит к рас­пределению потоков мощности в сети только с активным сопротивлением.

Р ассмотрим самый простой случай, когда все потоки Q равны нулю. Потери активной мощно­сти в сети являются квадратичной формой потоков актив­ной мощности в линиях, которую можно записать следую­щим образом: (1), где Р_В — вектор - столбец потоков активных мощностей в ветвях, порядок которого равен числу ветвей т; индекс «т» означает транспонирование; R_B — диагональная матри­ца активных сопротивлений ветвей порядка т, l-й элемент которой равен активному сопротивлению l-й ветви.

Для сети на рис. 13.2 потери мощности можно записать

в таком виде:

.

Первый закон Кирхгофа можно записать: (2), где Р - вектор-столбец активных мощностей в узлах, по­рядок которого равен числу независимых узлов п; М — первая матрица инциденций, число строк которой равно п, а число столбцов — числу ветвей т. Для сети на рис. 13.2

и первый закон Кирхгофа

Задача оптимизации и

в матричном виде имеет вид: определить (3) при выполнении условия (2). Это задача квадратичного программирования, так как целевая функция (1) - квадратичная форма, а ограни­чения (2) - система линейных алгебраических уравне­ний. Запишем функцию Лагранжа в матричном виде:

5.2 Оптимизация распределения перетоков мощности сложной электрической сети

, где - вектор-столбец множителей Лагранжа.

Для нашей сети при потоках Q, равных нулю .

Минимум функции Лагранжа определяется системой уравнений:

Второе уравнение - это уравнение первого закона Кирхгофа для Р, совпадающие с (2). Первое уравнение можно рассматривать как закон Ома для каждой из ветвей сети, напряжения в узлах которой равны . Покажем, что эти уравнения эквивалентны уравнениям уз­ловых напряжений.

Для этого выразим из первого и, подставив во второе и учитывая, что , по­лучим .

Последнее выражение перепишем так: (4), где G_y — матрица активных собственных и взаимных проводимостей узлов. Примем, что напряжения узлов в сети с r равны множителям Лагранжа, умноженным на : .

Тогда (4) — это уравнение узловых напряжений в сети только с r, для которой G_y — матрица активных уз­ловых проводимостей, Р — вектор узловых мощностей, — вектор узловых напряжений, деленный на .

Из всего этого следует, что задача оптими­зации потоков Р (3), (1) сводится к решению уз­ловых уравнений для сложной сети с активными сопротив­лениями.

Повторив подобный вывод выражений, можно получить аналогичный (4) результат для сложной сети, в кото­рой потоки Q не равны нулю.