24.2 Комплексная оптимизация режимов энергосистемы

1. Уравнение цели .

Вектор параметров Z разделяется на вектор незави­симых переменных и зависимых переменных

Тогда можно записать .

2. Уравнения связи включают:

– эквивалентные характеристики генераторных узлов вида , где – эквивалентный расход условного топлива;

– связи между параметрами X и Y, которые имеют вид Y(Х);

3. Уравнения ограничений, которые задаются в виде не­равенств

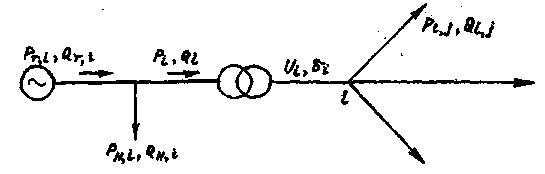
Задаются также балансовые ограничения по актив­ным и реактивным мощностям в виде системы уравне­ний установившегося режима (рис.).

Для каждого узла небаланс по мощности равен: , где и – функция небаланса по активной и реактивной мощностям.

Когда в стационарном режиме в узлах системы име­ется баланс, то , . Если в стационар­ном режиме изменить независимые переменные , , то появится небаланс и , . Меняя , , можно получить новый допустимый стацио­нарный режим для новых значений , . Задача и бу­дет заключаться в том, чтобы найти такое решение урав­нений установившегося режима, при котором .

4. Вычисление приведенного градиента. Решение считается оптимальным, если модуль градиент - вектора функции В (Х, Y) будет меньше заданного малого значения, т. е. .

1. Понятие оптимизации. Основные задачи оптимизации в электроэнергетике. Степени свободы электроэнергетической системы

2. Применение метода множителей Лагранжа при решении задач оптимизации в ЭЭ

3. Опт-е распределение перетоков мощности в замкнутых контурах эл. сети

4. Прим-ие м-да множителей Л. для опт-ии перетоков мощности в эл. сети

5. Оптимизация распределения перетоков мощности сложной эл. сети

6. Определение оптимального распределения нагрузки между ТЭС методом множителей Лагранжа. Относительные приросты ТЭС

7. Определение оптимального распределения нагрузки между ТЭС методом множителей Лагранжа. Структурная схема алгоритма

8. Наивыгоднейшее распределение нагрузки между ТЭС без учета потерь P. Физический смысл равенства относительных приростов

9. Определение опт. распределения нагрузки в энергосистеме с ГЭС и ТЭС методом множителей Лагранжа. Относит. приросты ТЭС и ГЭС

10. Размерность и физический смысл множителей Лагранжа в задачах оптимизации распределения нагрузки в энергосистеме

11. Оптимальное распределение нагрузки при постоянном напоре ГЭС и структурная схема алгоритма поиска данного распределения

12. Оптимальное распределение нагрузки при переменном напоре ГЭС

13. Оптимальное распределение нагрузки между агрегатами электростанций. Оптимальная последовательность включения агрегатов электростанций

14. Формулировка задачи оптимизации режима энергосистемы с позиций нелинейного программирования. Основные определения

15. Применение методов возможных направлений для поиска экстремума целевой функции при решении задач оптимизации в электроэнергетике

16. Применение метода наискорейшего спуска при решении задач опт-ии в ЭЭ

17. Способ вычисления оптимальной длины шага вдоль заданного направления спуска при решении задач оптимизации в электроэнергетике

18. Применение метода покоординатной оптимизации в электроэнергетике. Внешний и внутренний циклы метода

19. Применение градиентных методов оптимизации в электроэнергетике. Критерии сходимости. Градиентный метод + метод наискорейшего спуска

20. Применение градиентных методов оптимизации в электроэнергетике. Метод проектирования градиента

21. Учет ограничений в форме равенств при решении задач оптимизации в электроэнергетике. Приведенный градиент

22. Учет ограничений в форме неравенств при решении задач оптимизации в электроэнергетике. Метод штрафных функций

23. Оптимизация режима электроэнергетической системы методом Ньютона. Матрица Гессе. Геометрическая интерпретация аппроксимации ЦФ

24. Комплексная оптимизация режимов энергосистемы