18 Применение метода покоординатной оптимизации в электроэнергетике. Внешний и внутренний циклы метода

М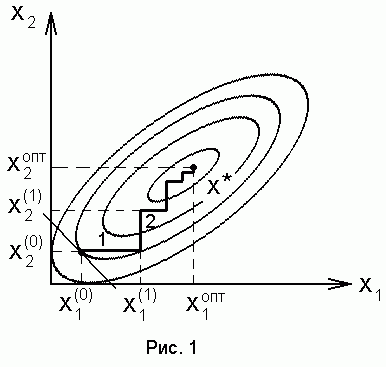 етод покоординатной оптимизации относится к наиболее простым по реализации ал­горитмам. Суть его заключается в том, что в качестве возможных направлений рассматриваются орты исходной системы координат

При этом N шагов по всем независимым переменным образуют внутренний цикл. Это означает, что на первом итерационном шаге минимизируется целевая функция F(x) при изменении только пер­вой переменной, а все остальные переменные остаются неизмен­ными. Если спуск осуществляется с отысканием оптимальной дли­ны шага, то

Н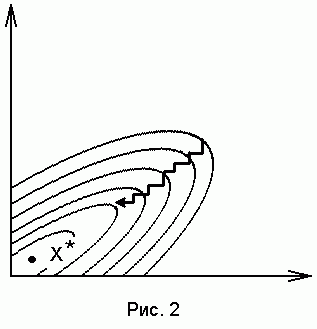 а втором шаге процедура повторяется для второй переменной: Частная минимизация по всем N переменным образует полный цикл, называемый внешним. Количество внешних циклов, т. е. пов­торений внутренних циклов, заранее неизвестно и определяется схо­димостью вычислительного процесса, которая зависит от свойств минимизируемой функции F(x) и выбора исходного приближения х°. На рис. 1 штриховой линией показана траектория спуска. Несмотря на простоту реализации и малый объем вычислений на шаге, часто от метода приходится от­казываться из-за неудовлетворительной сходимости. На рис. 2 приведена геометрическая интерпретация так называемой «овражной» функции для двумерной задачи F(x₁, х₂). Если «дно овра­га» не совпадает с направлением коорди­натных осей, то количество шагов становится неприемлемо большим.

19.1 Применение градиентных методов оптимизации в электроэнергетике. Критерии сходимости. Градиентный метод в сочетании с методом наискорейшего спуска

В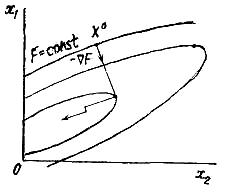 градиентных методах движение всегда осуществляется в направлении наи­большего убывания целевой функции . Вектор градиента определяется через производные функции F(x) по всем независимым переменным .

Таким образом, чтобы воспользоваться рекуррентным выраже­нием градиентного метода , необходимо на каждом шаге итерационного процесса вычислять значения производ­ных . Для организации скорейшего спуска необходимо определение оптимальной длины шага , которая в этом случае удовлетво­ряет условию . Это условие означает, что результирующий вектор спуска должен быть таким, чтобы новый градиент стал ортогонален предыдущему.

Рассмотрим два наиболее распространенных критерия окончания расчета, на основании которых можно судить о степени близости к экстремуму и к окончанию расчета.

Первый критерий основан на сопоставлении функции цели на двух соседних шагах k и к+1. Если убывание целевой функции мало, т. е. , где – заданная некоторая малая величина, то принимается, что найдено приближенное значение минимума F. Точность отыскания экстремума регулируется величиной : чем меньше , тем точнее решение, но тем больше потребуется итерационных шагов, так как при приближении к экстремуму сходимость методов возможных на­правлений замедляется.

Преимущество первого критерия заключается в простоте реали­зации, однако в некоторых случаях он не соответствует приближе­нию к экстремуму. Например, при отыскании минимума функции с оврагом, когда две соседние точки x^k+1 и x^k оказываются на дне оврага. Убывание целевой функции будет мало, хотя решение дале­ко не оптимально.

Более строгим является второй критерий — проверка длины гра­диента при отыскании абсолютного минимума F. Во втором критерии ис­пользуется тот факт, что в точке экстремума все частные