Приклад.

Обчислити площу фігури, обмеженої кривими і , та дожину дуги, що обмережує цю фігуру .

Обчислення в MathCAD:

Введемо функції та знайдемо точки перетину кривих.

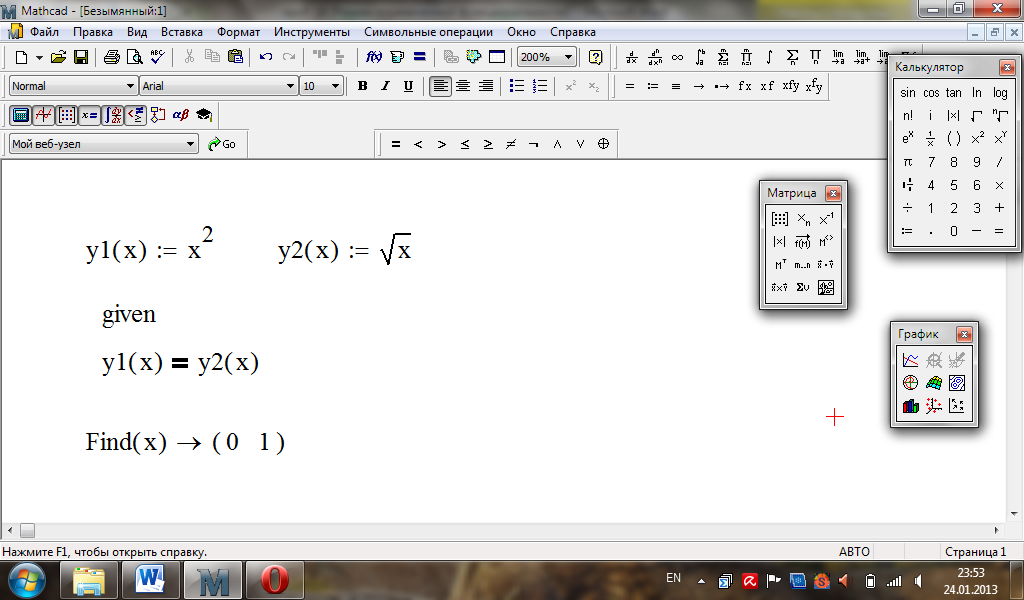або

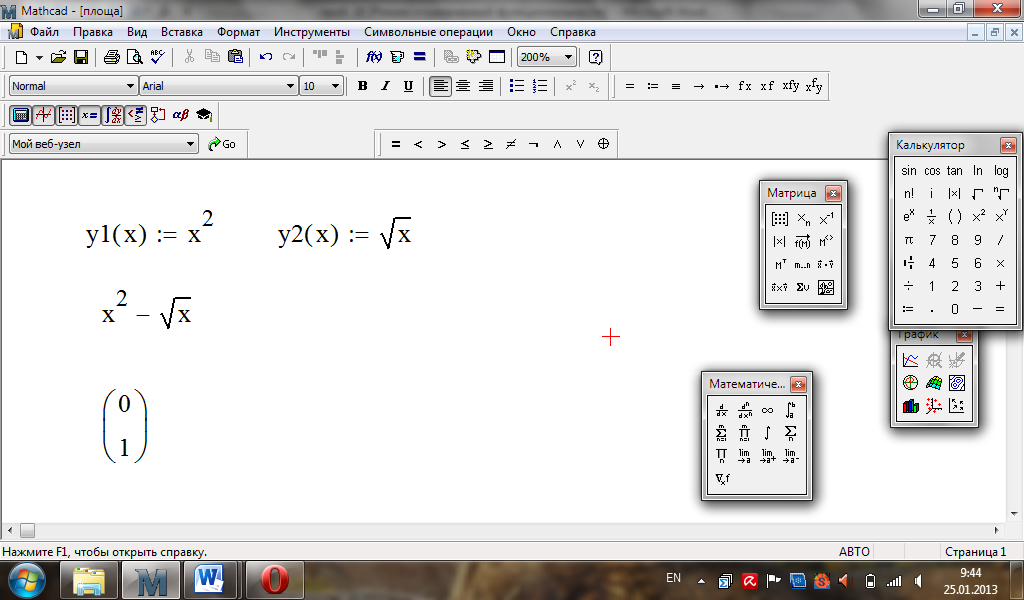
Побудова області:

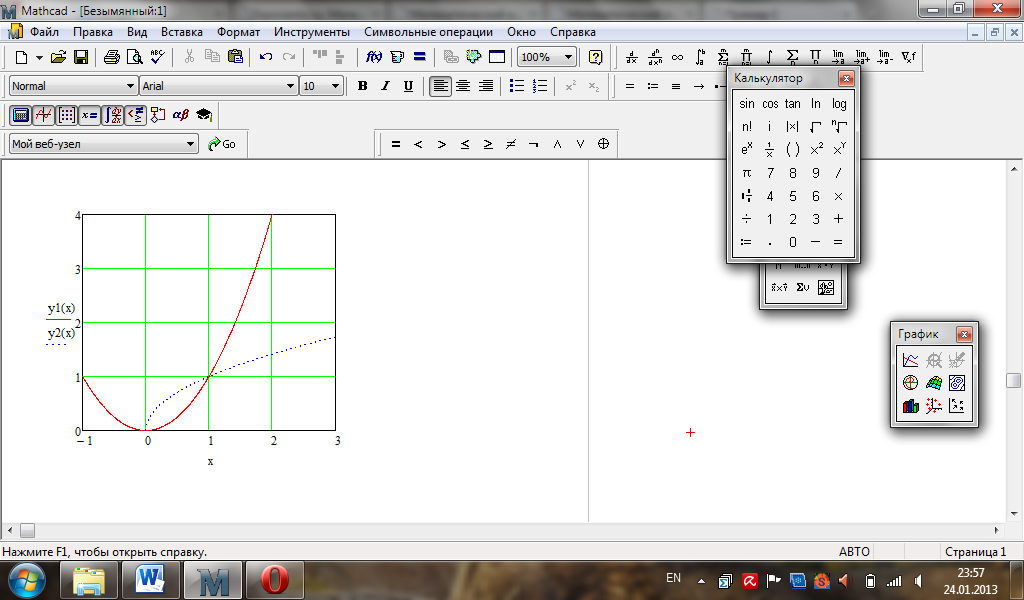
Обчислимо площу за формулою Ньютона – Лейбніца.

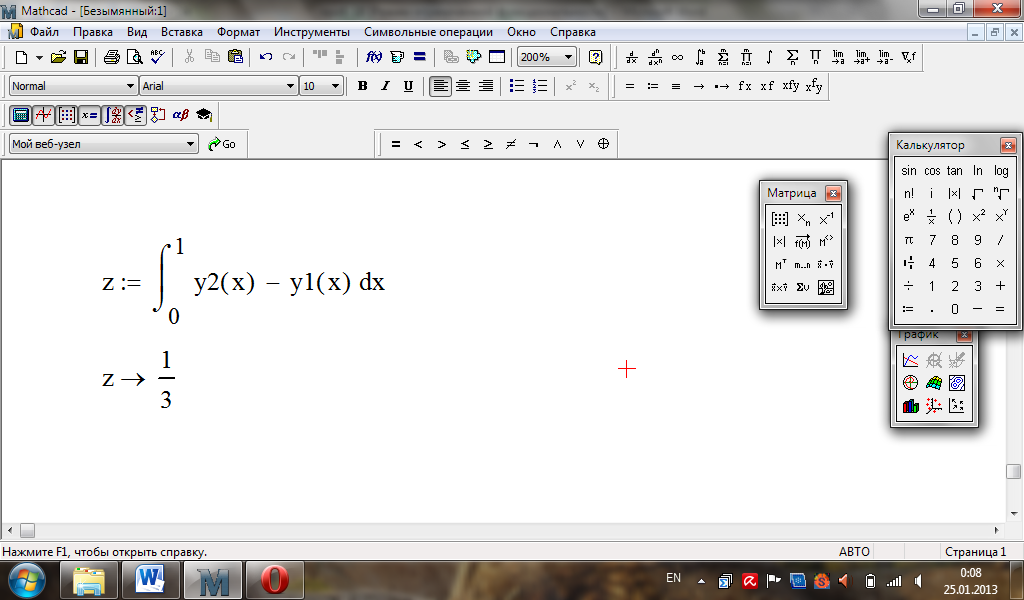
Обчислимо довжину дуги, що обмежує область (вона складається з двох частин).

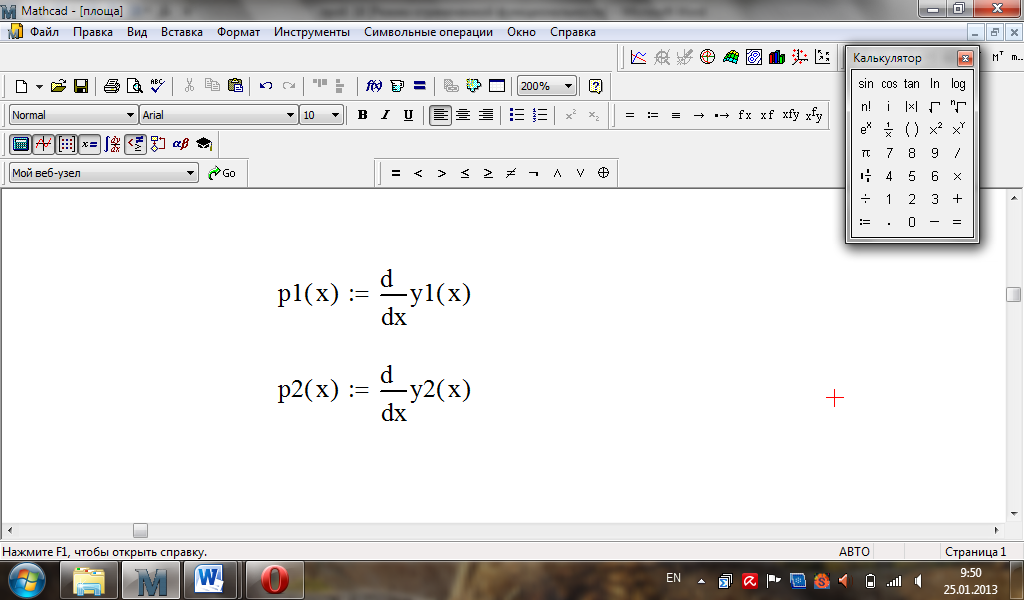
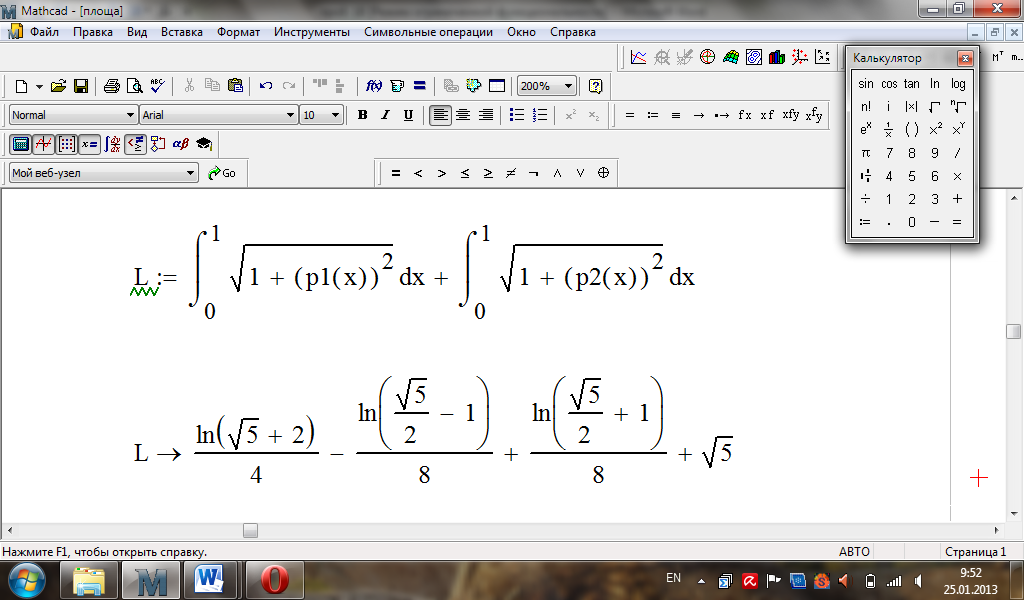
Аналогічні міркування, якщо функції занані параметрично або в полярних координатах.

Завдання до лабораторної роботи № 18.

Варіант	Завдання
1	1. а) і вісь ; б) одна арка циклоїди і вісь . 2. , якщо
2	1. а) , , ; б) . 2. , якщо .
3	1. а) ; б) . 2. , якщо .
4	1. а) , ; б) . 2. , якщо .
5	1. а) , ; б) . 2. , якщо .
6	1. а) , б) , . 2. , якщо .
7	1. а) ; б) . 2. , якщо .
8	1. а) ; б) 2. , якщо .
9	1. а) , ; б) , . 2. , якщо .
10	1. а) , ; б) одна арка циклоїди і вісь . 2. , якщо .
11	1. а) , ; б) . 2. Спіраль Архімеда від початку до кінця першого витка.
12	1. а) ; б) . 2. , якщо .
13	1. а) , ; б) . 2. , якщо
14	1. а) , ; б) . 2. , якщо .
15	1. а) ; б) . 2. , якщо .
16	1. а) , ; б) одна арка циклоїди і вісь . 2. , якщо .
17	1. а) , ; б) , вісь . 2. .
18	1. а) ; б) , , . 2. Спіраль Архімеда від початку до кінця першого витка.
19	1. а) ; б) , . 2. .
20	1. а) ; б) , , вісь . 2. .
21	1. а) ; б) , . 2. якщо .
22	1. а) ; б) , , вісь . 2. .
23	1. а) ; б) 2. одна арка циклоїди .
24	1. а) ; б) . 2. .
25	1. а) ; б) . 2. .
26	1. а) ; б) . 2. Спіраль Архімеда від початку до кінця другого витка.
27	1. а) ; б) . 2. .
28	1. а) ; б) . 2. .
29	1. а) ; б) . 2. .
30	1. а) ; б) . 2. .
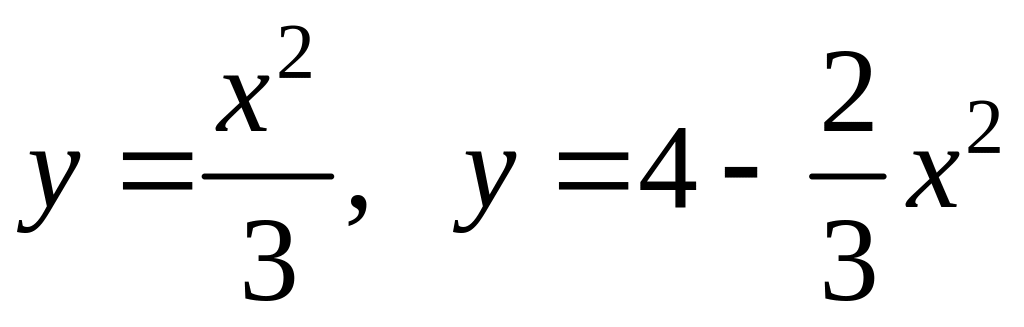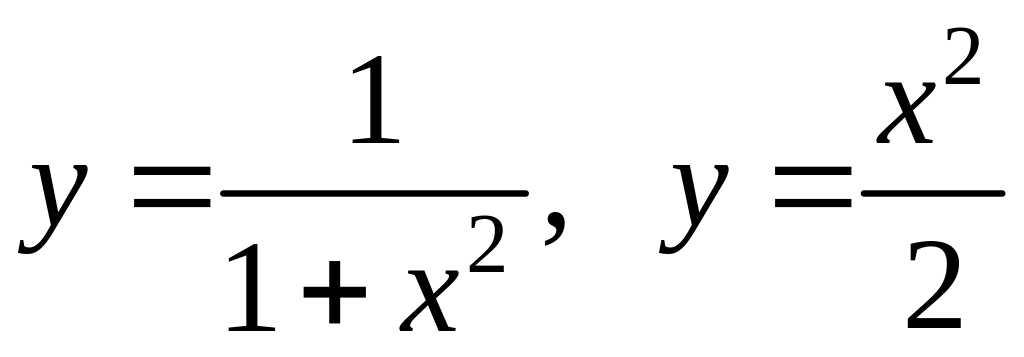