Геометрическое определение вероятности
В прямоугольник со сторонами 4 и 5 см вписан круг радиуса 1,5 см. Какова вероятность того, что точка, случайным образом поставленная в прямоугольник, окажется внутри круга?
Ответ:
.
Какова вероятность Вашей встречи с другом, если вы договорились встретиться в определенном месте, с 12.00 до 13.00 часов и ждете друг друга в течение 5 минут?
Ответ:
.
На отрезок ОА длины L числовой оси
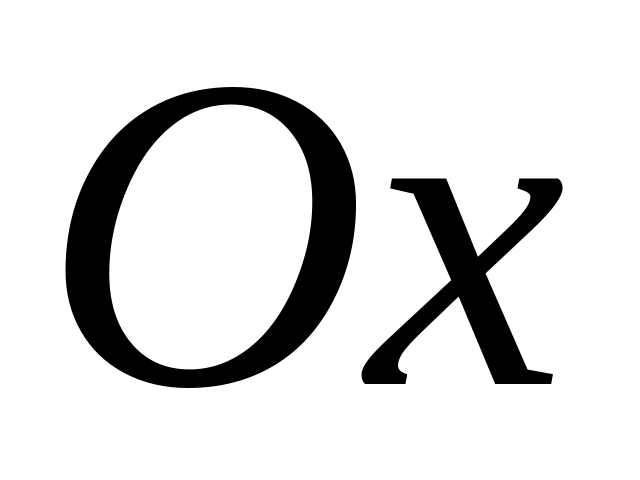наудачу поставлена точка В. Найдите
вероятность того, что меньший из отрезков
ОВ и ВА имеет длину, меньшую,
чем
.
Ответ:
.
Внутрь круга радиуса R наудачу брошена точка. Найдите вероятность того, что точка окажется внутри вписанного в круг квадрата.
Ответ:
.
На отрезке длины L наугад поставлены две точки x и y. Найдите вероятность того, что расстояние между ними меньше
и
.
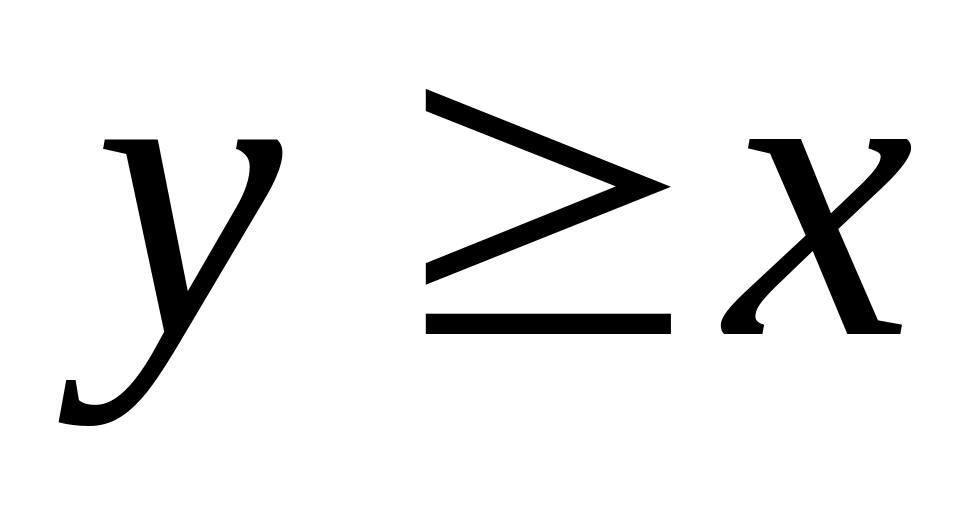Ответ: 0,375.
На отрезке длины L наугад поставлены две точки x и y. Найдите вероятность того, что расстояние между ними меньше
.
Ответ: 0,75.
Быстро вращающийся диск разделен на четное число равных секторов, попеременно окрашенных в белый и черный цвет. По диску производится выстрел. Найдите вероятность того, что пуля попадет в один из белых секторов.
Ответ: 0,5.
На плоскость с нанесенной сеткой квадратов со стороной
наудачу брошена монета радиуса
.
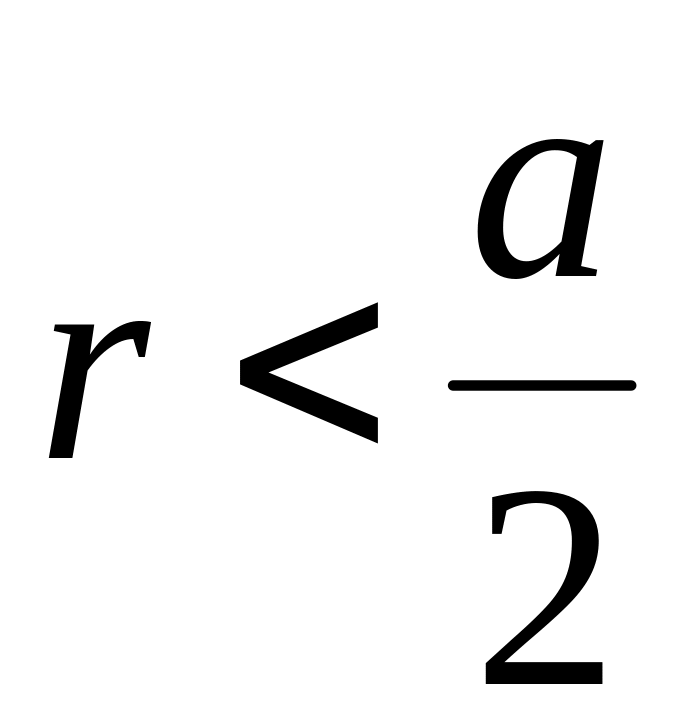Найдите вероятность того, что монета
не пересечет ни одной из сторон квадрата.
Ответ:
.
На плоскость, разграфленную параллельными полосами шириной 2d, расстояние между осевыми линиями которых равно 2D, наудачу брошен круг радиуса r (
).
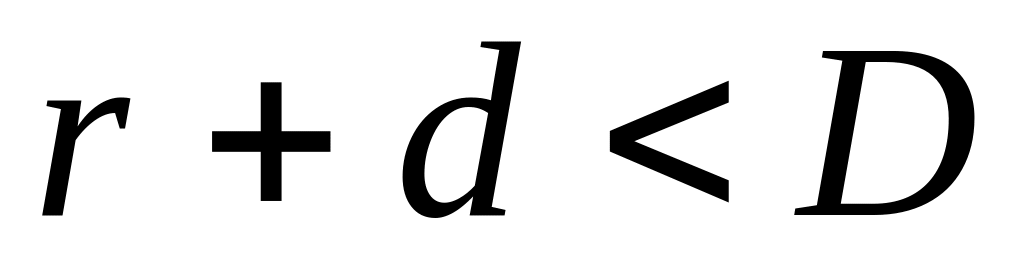Найти вероятность того, что круг
пересечет некоторую полосу.
Ответ:
.
Задачи на формулу Бернулли
Из 100 аккумуляторов за год хранения 7 выходит из строя. Наудачу выбирают 5 аккумуляторов. Определить вероятность того, что среди них 3 исправных.
Ответ:
0,0394.
Устройство, состоящее из пяти независимо работающих элементов, включается на время Т. Вероятность отказа каждого из них за это время равна 0,2. Найти вероятность того, что откажут:
а) три элемента (событие A);
б) не менее четырех элементов (событие B);
в) хотя бы один элемент (событие C).
Ответ:
0,0512;
0,00672;
0,67232.
В урне 20 белых и 10 черных шаров. Вынули 4 шара, причем каждый вынутый шар возвращают в урну перед извлечением следующего и шары в урне перемешивают. Найти вероятность того, что из четырех вынутых шаров окажется 2 белых.
Ответ:
.
Определить вероятность того, что в семье, имеющей 5 детей, будет не больше трех девочек. Вероятности рождения мальчика и девочки предполагаются одинаковыми.
Ответ:
.
Среди деталей, обрабатываемых рабочим, бывает в среднем 4% нестандартных. Найти вероятность того, что среди взятых на испытание 30 деталей две будут нестандартными.
Ответ: 0,202.
При каждом отдельном выстреле из орудия вероятность поражения цели равна 0,9. Найти вероятность того, что из 20 выстрелов число удачных будет не менее 16 и не более 19.
Ответ: 0,834.
Независимые испытания продолжаются до тех пор, пока событие А не произойдет k раз. Найти вероятность того, что потребуется n испытаний, если в каждом из них
.
Ответ:
.