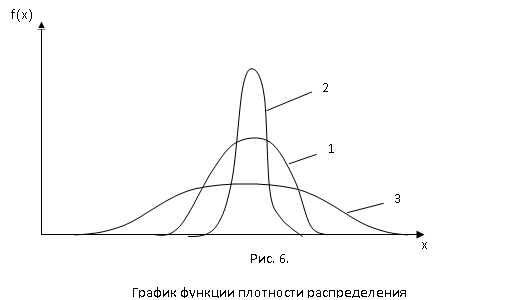
Плотность распределения случайной величины – общее понятие, графическое выражение
Мерой
остроты графика функции плотности
распределения является
- центральный момент четвертого порядка
(7)
(8)
Оценки моментов 3 и 4 порядков используются для решения вопроса о соответствии выборочных данных определенному типу распределения. Для этого обычно используют производные от них показатель асимметрии (А) и показатель эксцесса (Е) :
(9)
В формуле для Е цифра 3 отнимается, т. к. для симметричного распределения Е равен нулю.
Частота, частость, накопленная частость
Частота – число появлений событий в сери испытаний.
Частость – отношения числа поялений событий к общему числу событий.
Накопленная частость – Сумма всех частостей по классам, где значения случайной величины( т.е.е исследуемого признака) будет меньше заданного значения переменной х.
Среднее значение случайной величины, медиана, мода
Среднее
значение случайной величины –
арифметический корень из дисперсии,
т.е.
σ(X) =
.
Мода
– ее наиболее вероятное значение (рис.
2.3), а модой непрерывной случайной
величины – значение, при котором
плотность вероятности максимальна
(рис. 2.4).
Медиана — это такое значение признака, которое разделяет ранжированный ряд распределения на две равные части — со значениями признака меньше медианы и со значениями признака больше медианы. Для нахождения медианы, нужно отыскать значение признака, которое находится на середине упорядоченного ряда.
Дисперсия и её производные
Дисперсией 
случайной
величины 
называется
математическое ожидание квадрата
отклонения случайной величины от ее
математичекого ожидания *:
|
Показатели асимметрии, эксцесса
Асимметрия – это свойство распределения выборки, которое характеризует несимметричность распределения случайной величины. На практике симметричные распределения встречаются редко и чтобы выявить и оценить степень асимметрии, вводят следующую меру (третий центральный момент) Показатель асимметрии:
или
.
Для сравнения асимметрии в нескольких рядах используют относительный показатель асимметрии.
или
Величина
может быть положительной и отрицательной.
Если 
,
то на графике такой ряд будет иметь
вытянутость вправо (правосторонняя
асимметрия), если 
,
то вытянутость влево (левосторонняя
асимметрия).
Эксцесс – это мера крутости кривой распределения.
Основные статистические законы распределения, используемые в геологии
В геологии ограничиваются использованием четырех основных теоретических законов распределения случайной величины: нормального, логнормального или логарифмически для непрерывных случайных величин и биноминального и Пуассона для дискретных.
Нормальное распределение
Нормальное распределение – это наиболее часто встречающееся в статистике и теории вероятностей распределение.
Нормальное распределение характеризуется двумя параметрами – математическим ожиданием и дисперсией. Оно симметрично относительно математического ожидания, поэтому его математическое ожидание, мода и медиана совпадают. В условиях нормального закона распределения вероятность значений, отличающихся от математического ожидания больше, чем на 3 стандартных отклонения настолько мала, что попадание их в выборку ограниченного объема можно считать событием практически невозможным (правило «трех сигм»), а большинство выборочных значений (95,45%) будет находится в интервале от -2 до +2 (рис. 7). Другими словами, 95,45% и 99,73% всех независимых наблюдений из нормального распределения лежит в радиусе 2 –х и 3 – х стандартных отклонений от среднего значения.
Закон больших чисел.
В теории вероятностей под «законом больших чисел» понимается группа математических теорем, каждая из которых устанавливается факт приближения средних характеристик большого числа наблюдений к некоторым определенным постоянным. К нему также относится группа теорем, называемых центральной предельной теоремой. Эта группа теорем касается предельных законов распределения. Одной из наиболее важных является теорема Чебышева, устанавливающая в точной количественной форме свойство устойчивости среднего арифметического: при достаточно большом числе независимых опытов среднее арифметическое наблюденных значений случайной величины сходится по вероятности к ее математическому ожиданию. Центральная предельная теорема посвящена установлению условий, при которых возникает нормальный закон распределения.
Логарифмически нормальный (логнормальный) закон
Итак, функция логнормального распределения соответствует функции нормального распределенья, где вместо значений самой случайной величины вводятся характеристики, рассчитанные для ее логарифмов: При логнормальном распределении нормальному закону подчинены не сами значения случайной величины, а их логарифмы. Поэтому сначала находят натуральные (или десятичные) логарифмы всех значений случайной величины, а затем все операции проводят с логарифмами, как с обычными числами: вычисляют их статистические характеристики и по таблицам нормального распределения определяют вероятности. В случае, если в исходной совокупности встречаются нулевые значения, их заменяют минимальными или половиной чувствительности анализа, поскольку логарифмировать нулевые значения не представляется возможным.
Таблицы для логнормального распределения отсутствуют, поэтому теоретическую кривую плотности вероятности строят непосредственно по формуле (17), где - математическое ожидание и стандарт логарифмов значений. Как и нормальное распределение, логарифмически нормальное распределение имеет два параметра.
Появление логнормального распределения, как и нормального, связано с воздействием на исследуемое свойство множества факторов. Однако сила воздействия каждого фактора не одинакова, а пропорциональна изменению силы проявления данного фактора.
Биноминальный закон распределения.
Биноминальное распределение является важнейшим дискретным распределением, т.е. распределением, которое сосредоточено всего лишь в нескольких точках. Этим точкам биноминальное распределение присваивает ненулевые вероятности. Таким образом, биноминальное распределение отличается от рассмотренных выше распределений, которые являются непрерывными. Параметрами биноминального распределения являются вероятность успеха р и число испытаний n.
Биноминальный закон распределения называется также схемой Бернулли, который открыл этот закон.
Закон распределения Пуассона
Если число испытаний велико, а вероятность появления случайного события в каждом испытании очень мала, то для описания вероятностей того, что событие А в серии из п испытаний произойдет m раз.