2.1.2 Задание 6

Построить область устойчивости замкнутой системы в плоскости параметров, указанных в таблице 7.

Таблица 7

Номер задания	Передаточная функция W(p)	Параметры	Номер задания	Передаточная функция W(p)	Параметры
1			14
2			15
3			16
4			17
5			18
6			19
7			20
8			21
9			22
10			23
11			24
12			25
13			26

2.1.3 Пример выполнения задания 6

Дано: передаточная функция разомкнутой системы

Построить область устойчивости в координатах

Решение

Запишем характеристический полином замкнутой системы:

Составим определитель Гурвица:

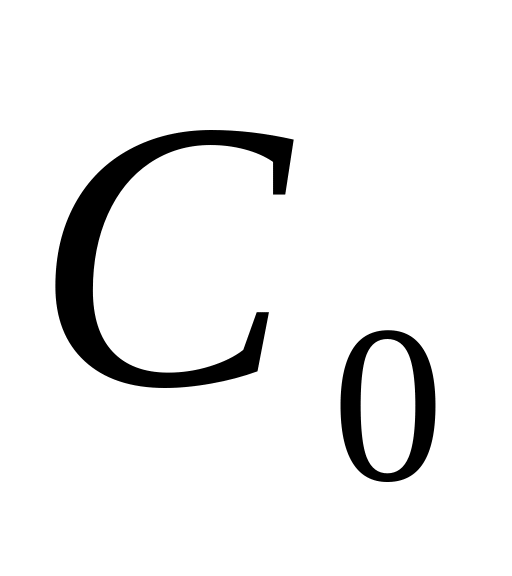
		0
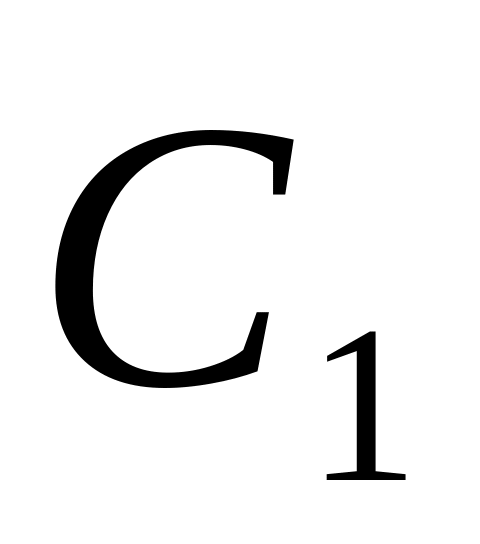
		0
0	0

Значит, должны выполняться два условия:

1. .

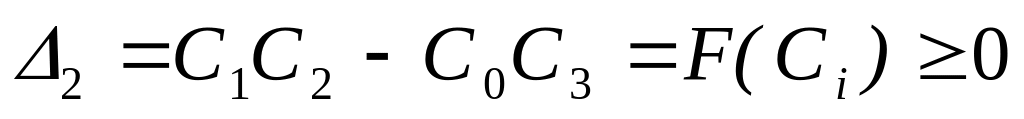2. Δ₂ = С₁С₂ – С₀ С₃ = F(C_i) >= 0.

Критерием устойчивости является:

Значит,

Область устойчивости приведена на рисунке 6.

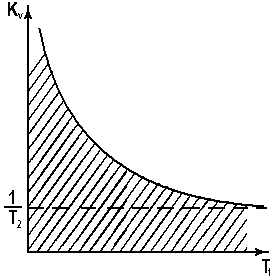
Рисунок 6 – Область устойчивости

2.1.4 Задание 7

Построить годограф характеристического вектора замкнутой системы. Пользуясь критерием Михайлова, определить устойчивость системы, если известны исходные данные (таблица 8).

Таблица 8

Номер задания	Передаточная функция W(p)	Номер задания	Передаточная функция W(p)
1		14
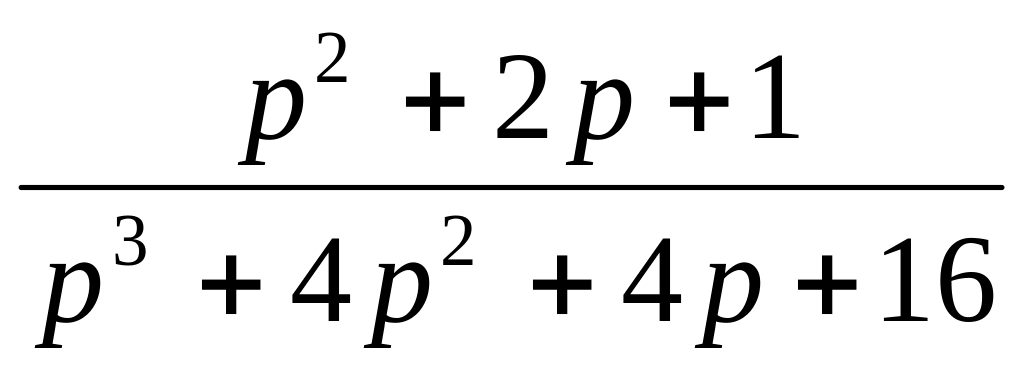
2		15
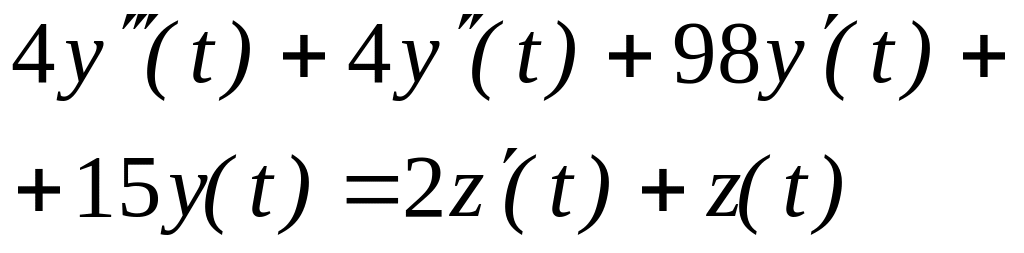
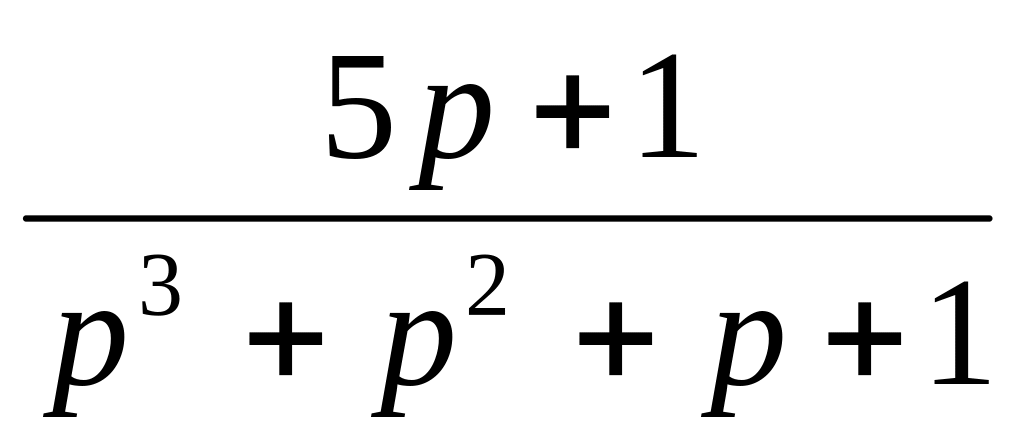
3		16
4		17
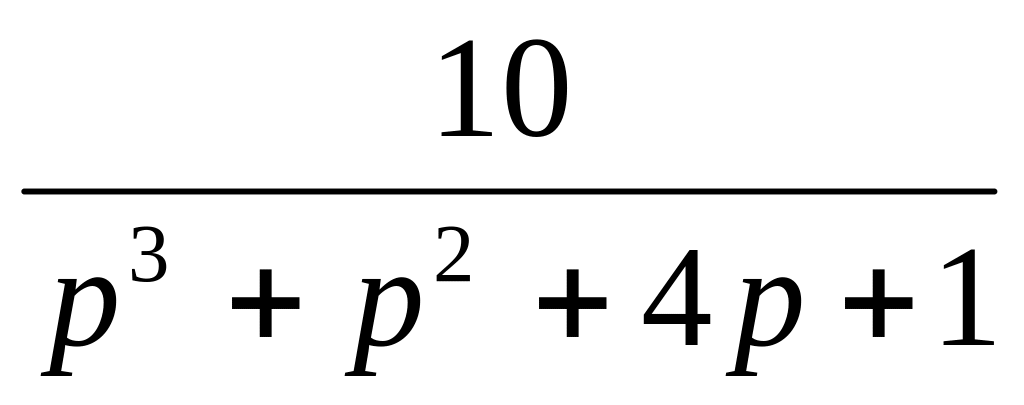
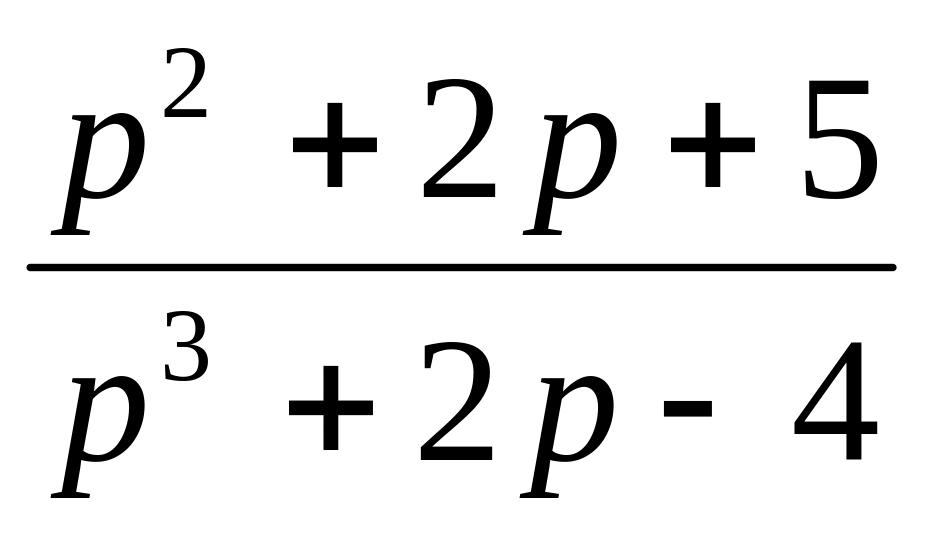
5		18
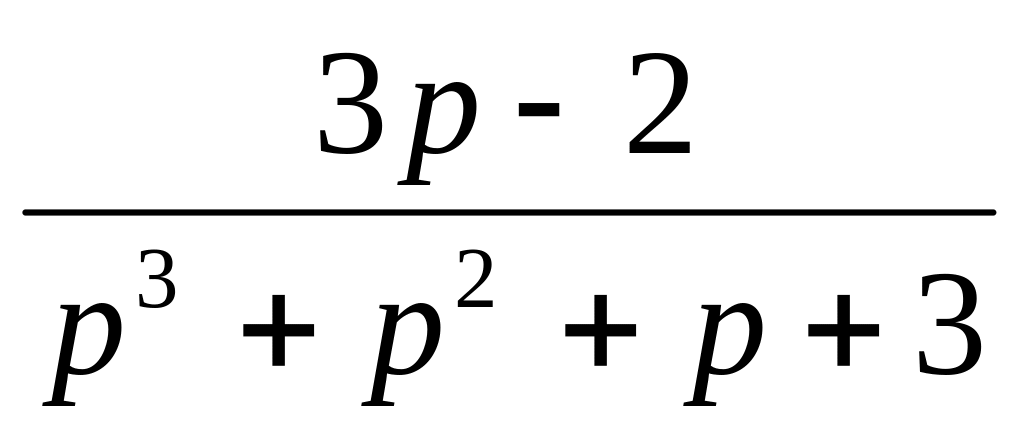
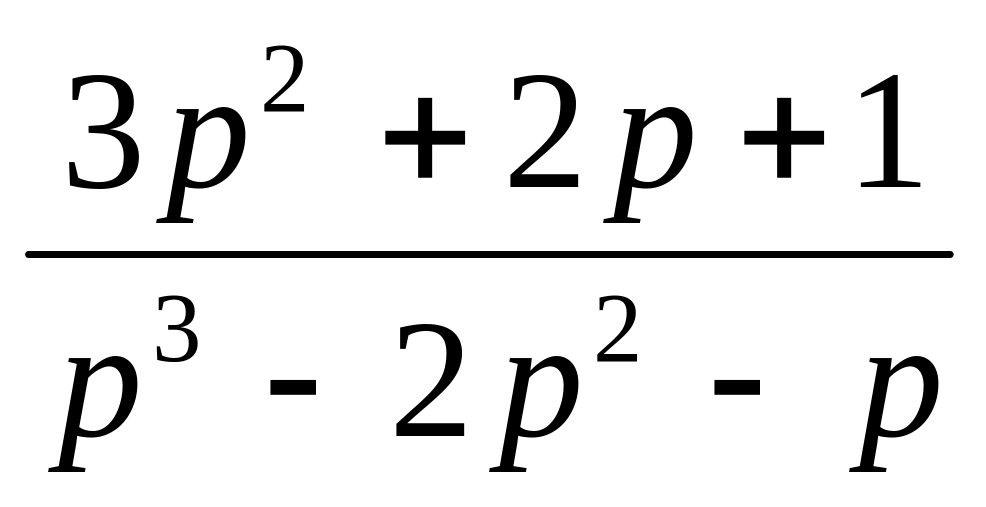
6		19
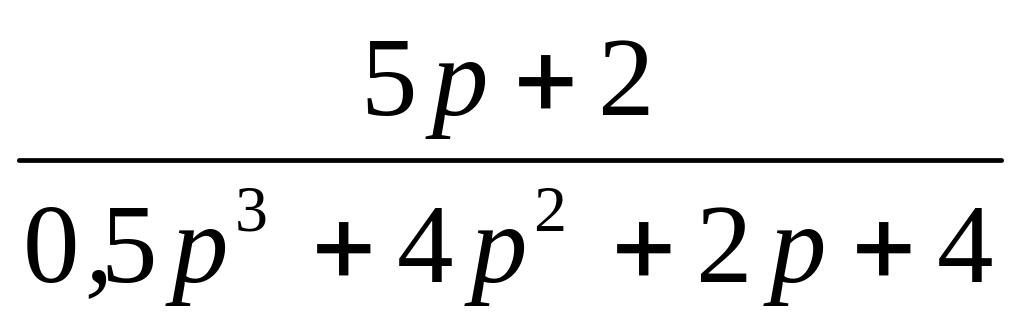
7		20
8		21
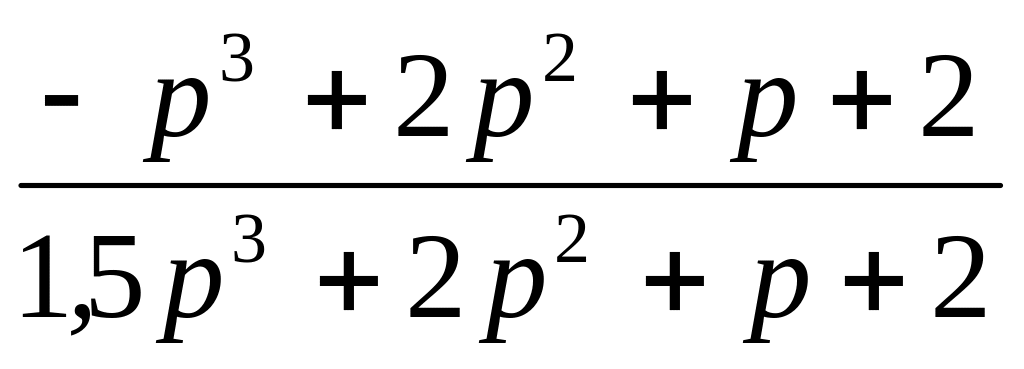
9		22
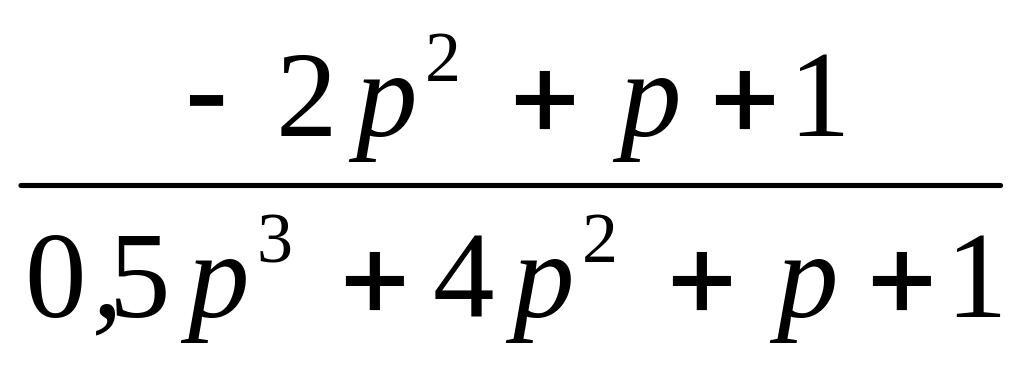
10		23
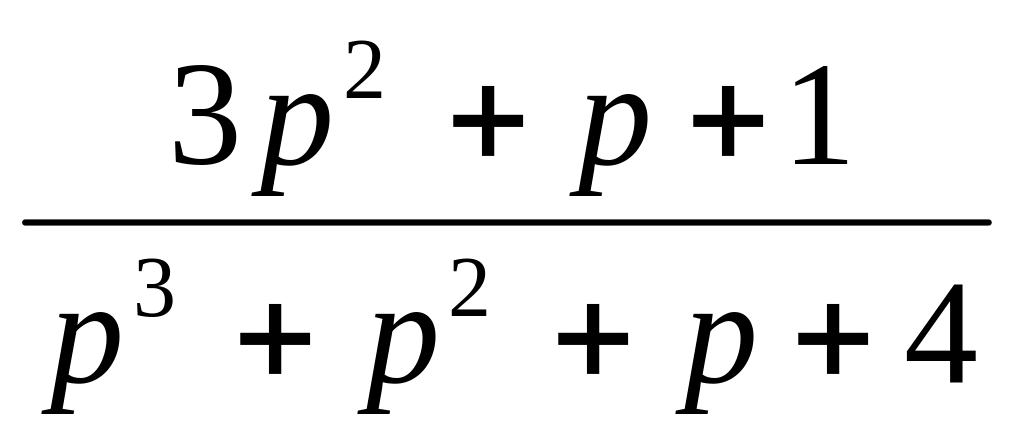
11		24
12		25
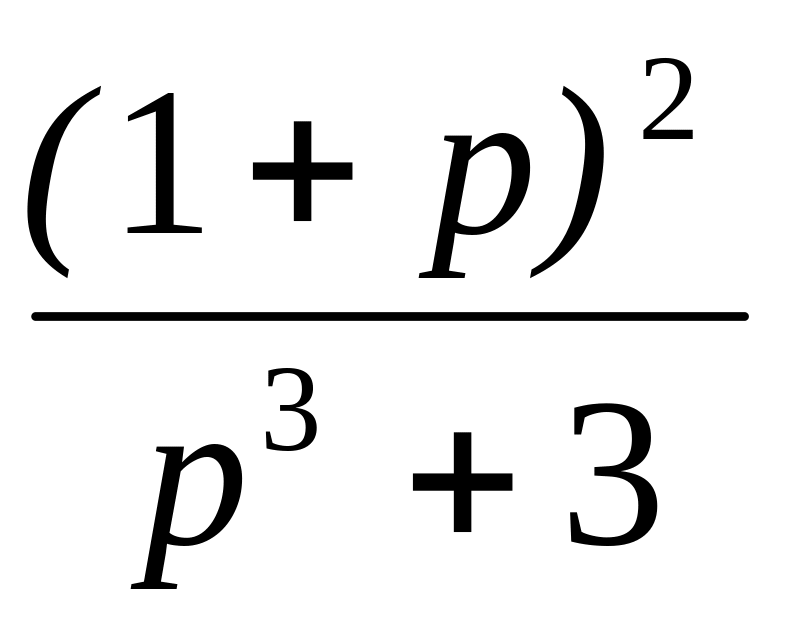
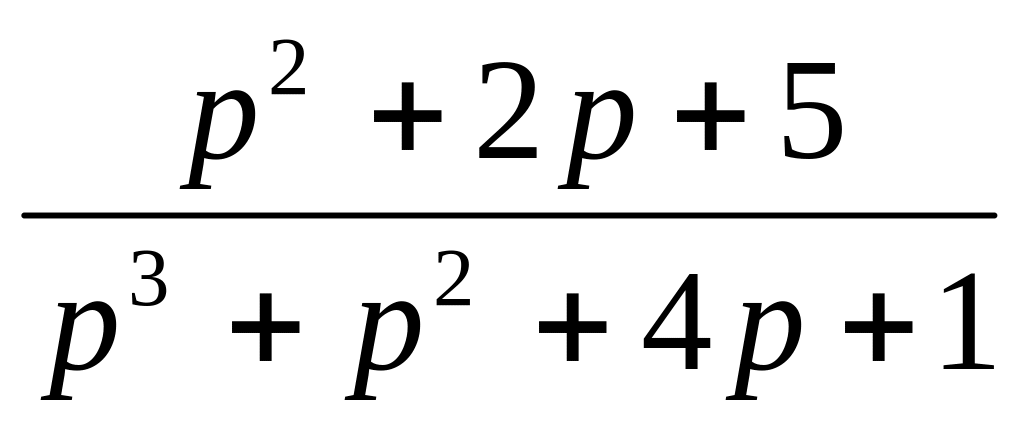
13		26