2.1.2 Пример выполнения задания 1

Дано:

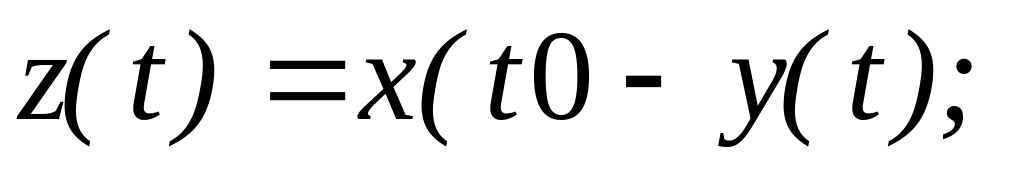1. 2) 3)

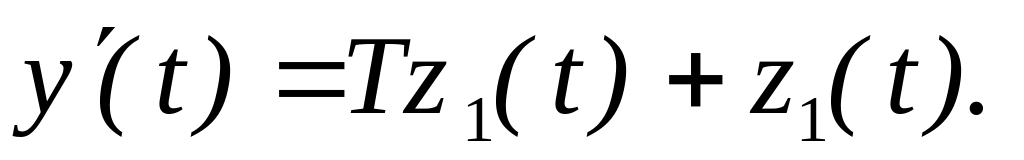
Определить передаточные функции.

Составленная структурная схема приведена на рисунке 1.

f (t)

+

z(t) k₁z(t) z ₁(t) y’(t) y(t)

x(t) _

+ +

k₂z(t)

Р исунок 1 – Структурная схема, составленная по дифференциальным

уравнениям

По структурной схеме запишем передаточные функции.

а) разомкнутой системы:

б) замкнутой системы:

в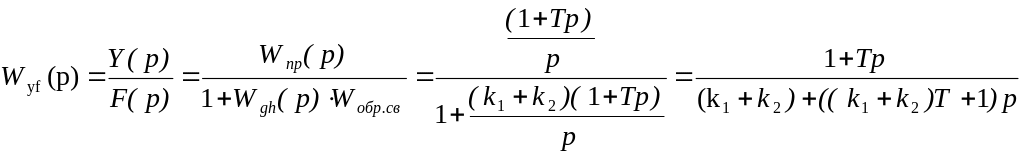 ) по возмущению f(t):

2.1.3 Задание 2

Для заданной передаточной функции системы, приведенной в таблице 3, записать математические зависимости и построить следующие частотные характеристики:

а) амплитудно-фазовую частотную характеристику W(jω);

б) амплитудную частотную характеристику A(ω);

в) фазовую частотную характеристику φ(ω);

г) вещественную частотную характеристику P(ω);

д) мнимую частотную характеристику Q(ω).

Таблица 3

Номер задания	Передаточная функция W(p)	Номер задания	Передаточная функция W(p)
1		14
2		15
3		16
4		17
5		18
6		19
7		20
8		21
9		22
10		23
11		24
12		25
13		26

Примечание. В передаточной функции заменить р на jω и выделить вещественную и мнимую часть: W(jω)=P(ω)+jQ(ω). Тогда А(ω)= , φ(ω) = arctg .

Построить графики полученных математических зависимостей при изменении ω от 0 до (графики можно строить с использованием прикладных программ MathCad, MATLAB).