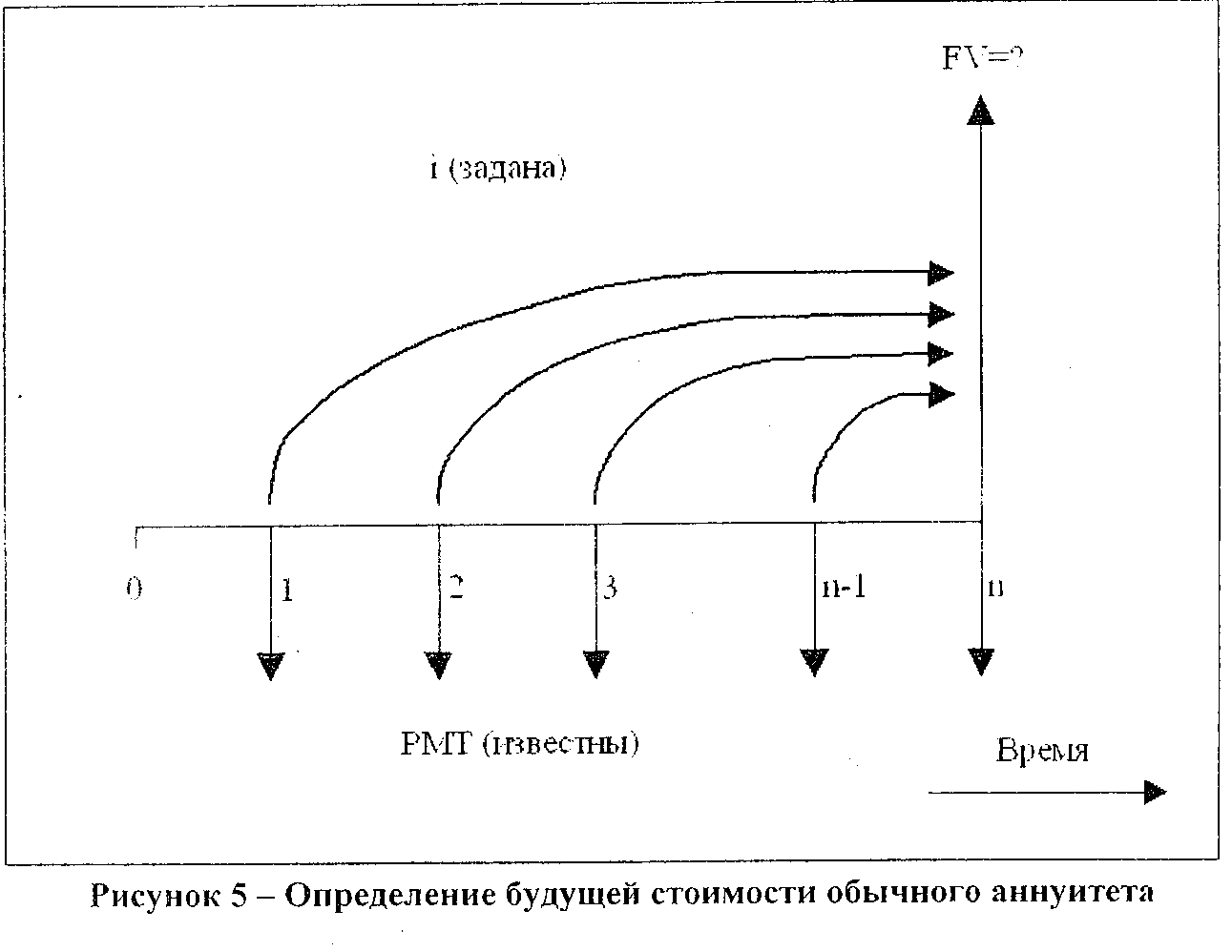
Накопление денежной единицы за период
Накопление денежной единицы за период – третья функция денег. Экономический смысл этой функции – какая сумма будет накоплена на счете при заданной ставке, если регулярно в течении определенного периода времени откладывать на счет одну денежную единицу.
PMT – периодический равновеликий платеж.
Расчет будущей стоимости обычного аннуитета
а) при начислениях в конце каждого года:
(8)
б) при начислениях, осуществляемых чаще, чем один раз в год:
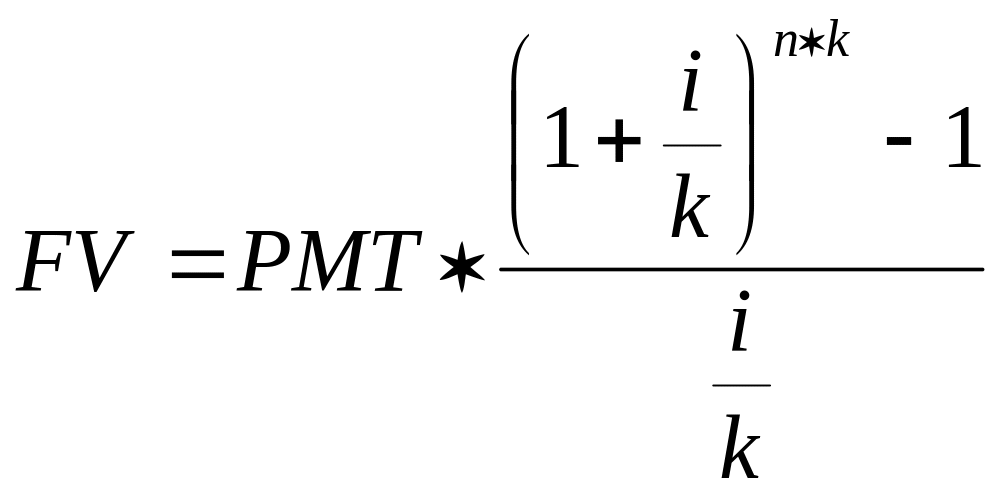(9)
Расчет будущей стоимости авансового аннуитета (в начале года, месяца)
а) при платежах, осуществляемых один раз в год:
(10)
б) при платежах, осуществляемых чаще, чем один раз в год:
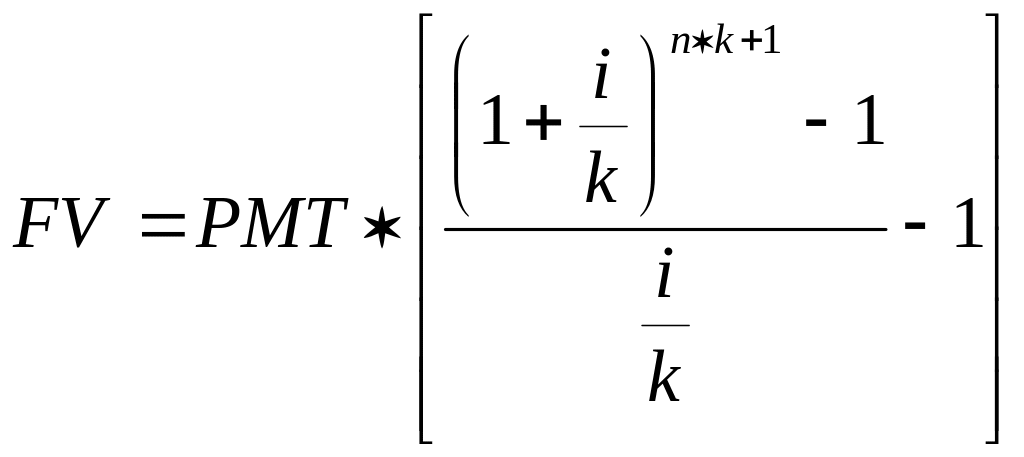(11)
Задача 3. Определить сумму, которая будет накоплена на счете, приносящем 12% годовых к концу 16 месяца, если ежемесячно откладывать на счет 2000 рублей.
а) в конце месяца;
б) в начале месяца.
Решение:
а) формула (9)
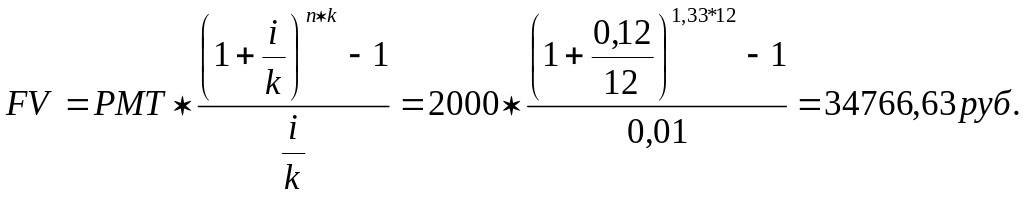
б) формула (11)
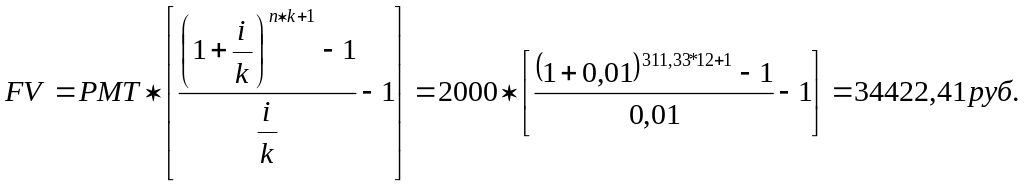
Ответ: а) FV = 34766,63руб.
б) FV = 34422,41 руб.
1.4 Фонд возмещения
Фонд возмещения – четвертая функция денег. Данная функция показывает, сколько нужно откладывать на счет регулярно в течение определенного периода времени, чтобы заданной ставке дохода иметь на счете к концу этого срока одну денежную единицу.
а) при платежах, осуществляемых один раз в год:
(12)
б) при платежах, осуществляемых чаще одного раза в год:
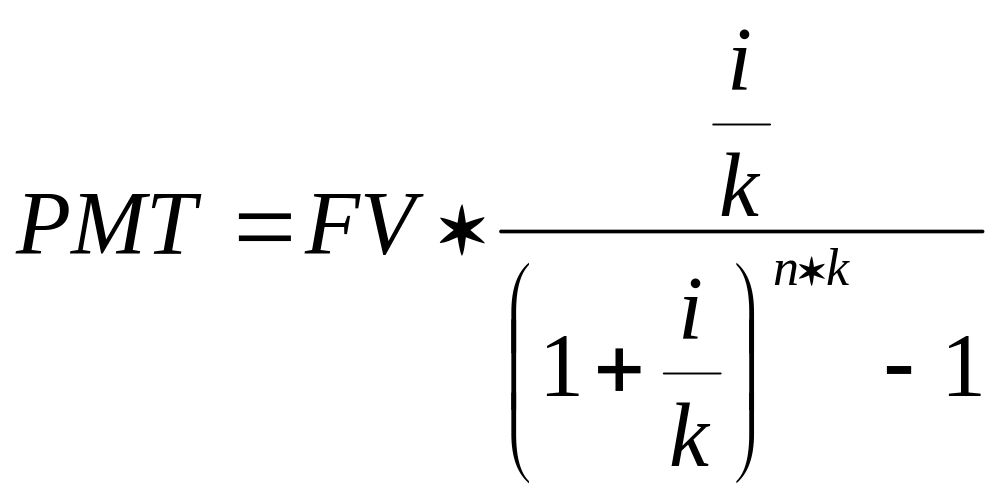(13)
- фактор
фонда возмещения.
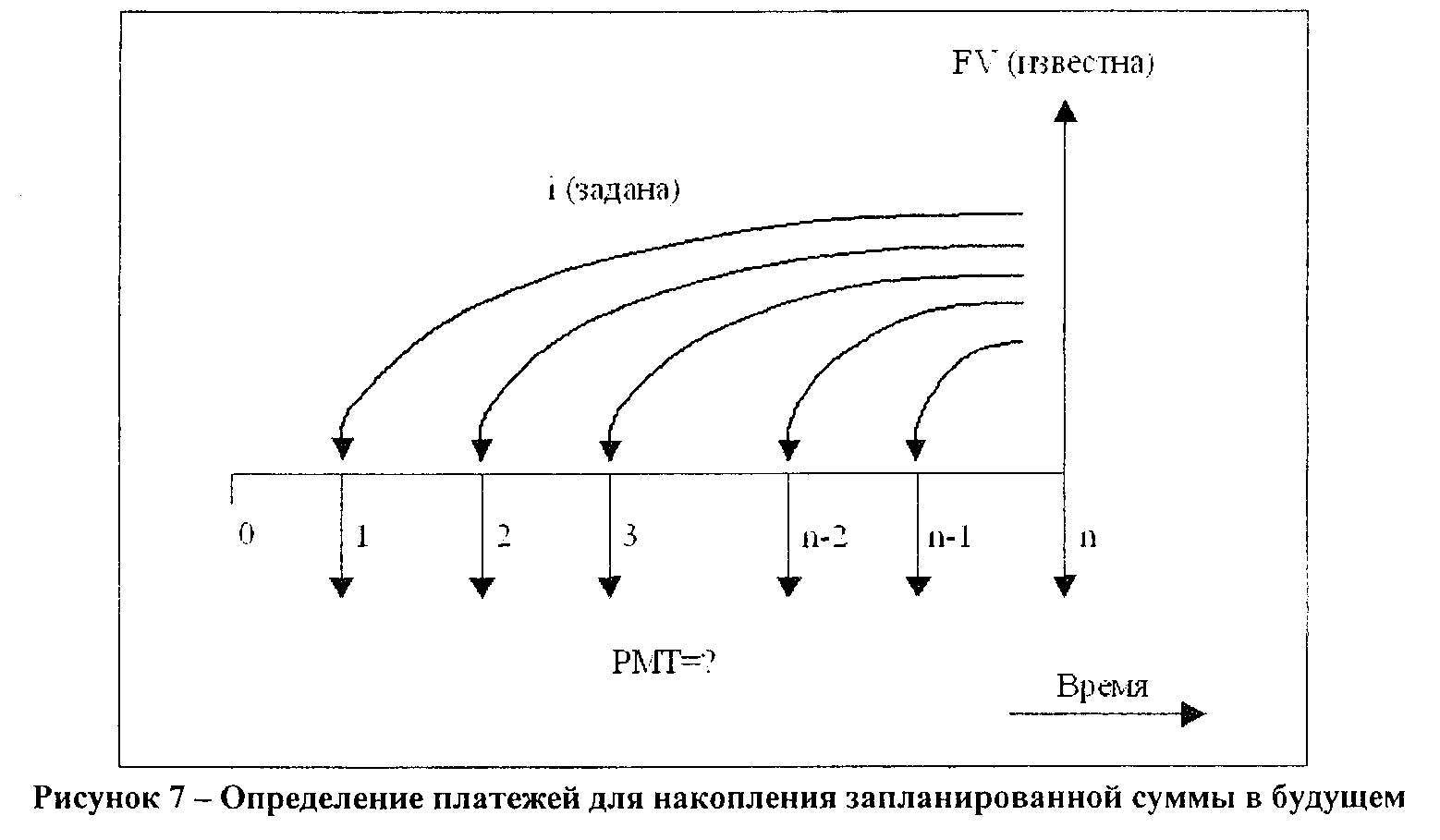
Задача 4. Определить сумму платежей, чтобы к концу 16-ти лет иметь на счете, приносящем 11% годовых, 20 000 рублей. Платежи осуществляются:
1) ежегодно k = 1 ,
2) ежемесячно k = 12.
Решение:
1)
2)
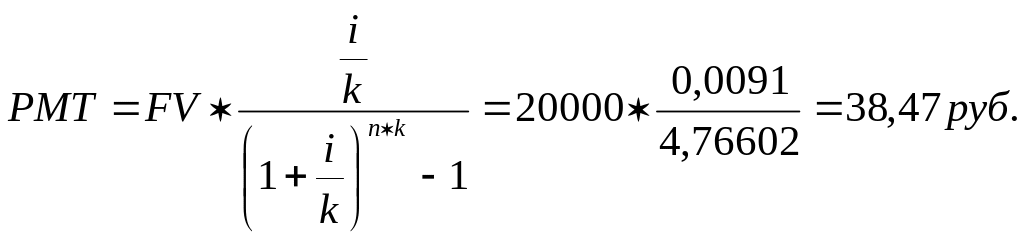
Ответ: 1) PMT = 510,33 руб.
2) PMT = 38,47 руб.
1.5 Взнос на амортизацию единицы
Взнос на амортизацию – пятая функция денег. Под амортизацией в данном случае понимают процесс погашения долга с течением времени. Данная функция показывает, какими должны быть аннуитетные или равновеликие платежи в счет погашения кредита в одну денежную единицу, выданного под определенный процент на определенный срок. Функция используется для определения обязательных периодических платежей, необходимых для погашения (возврата) кредита в течение установленного срока.
а) при платежах, осуществляемых один раз в год:
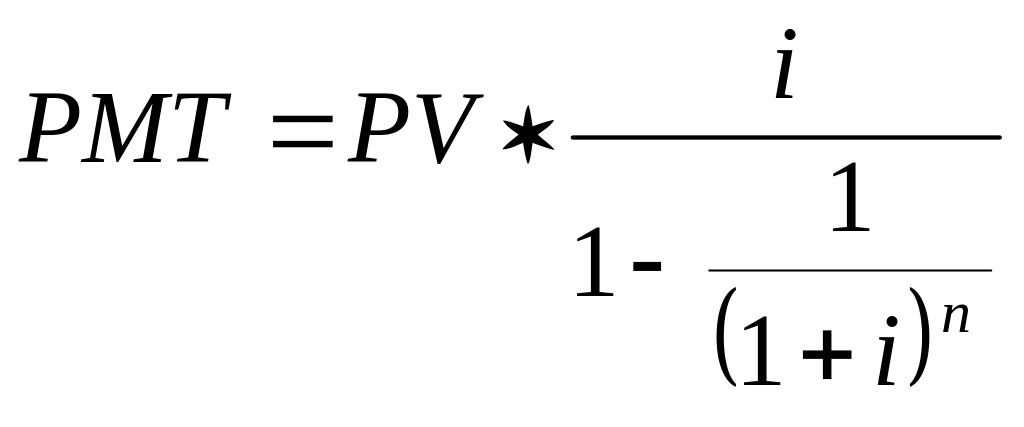(14)
б) при платежах, осуществляемых чаще одного раза в год:
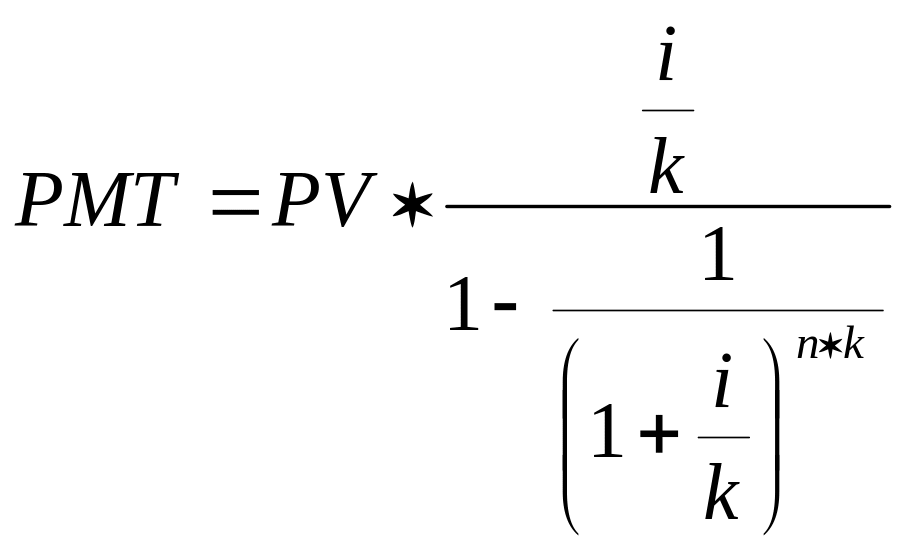(15)
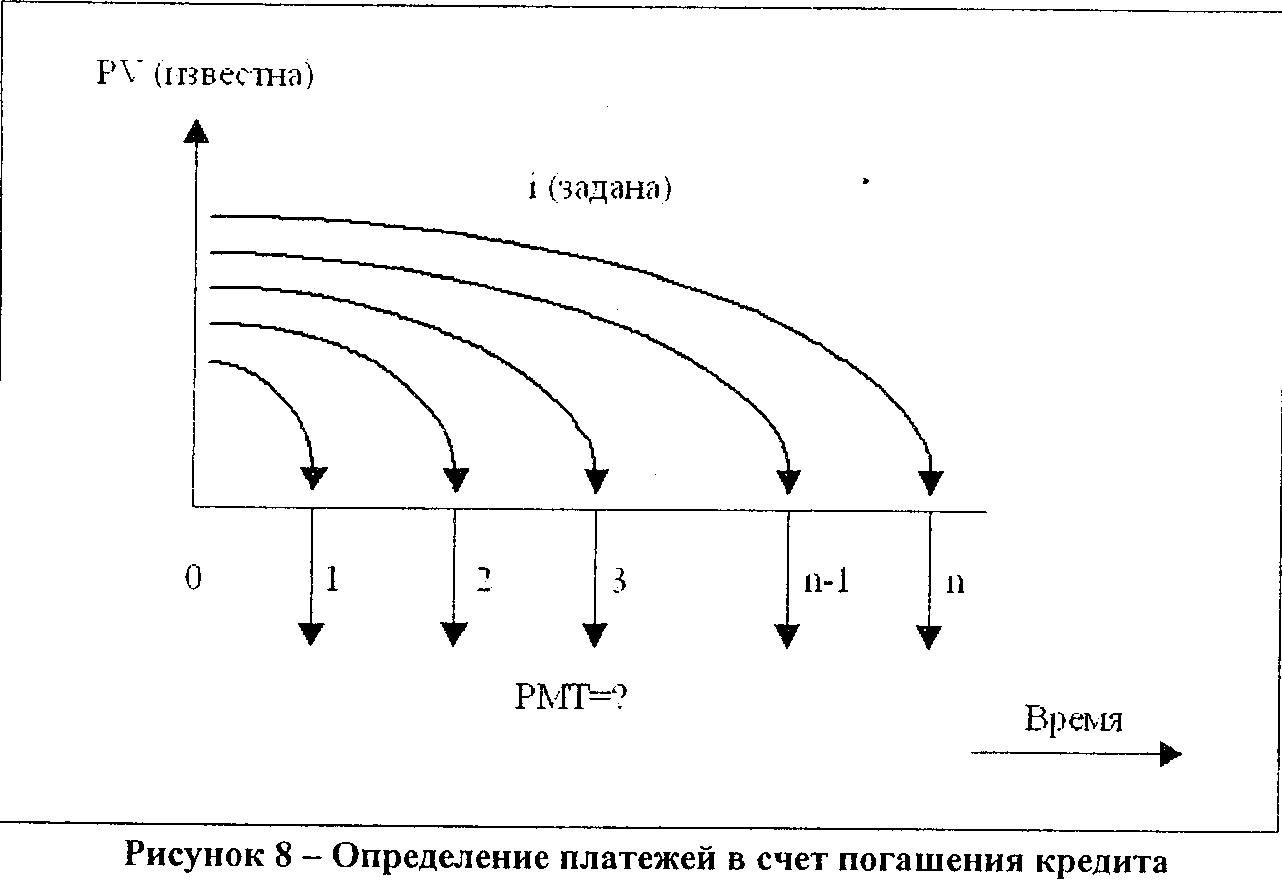
Задача 5. Кредит в размере 130 000 рублей выдан на 6 лет под 15% годовых. Определить размер аннуитетных платежей. Погашение кредита осуществляется ежемесячно.
Решение:
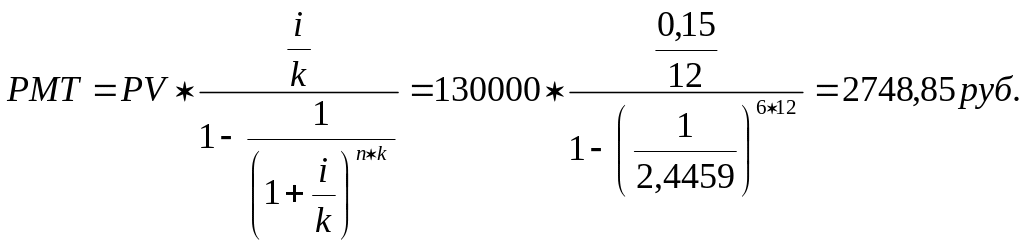
Ответ: PMT = 2748,85 руб.
1.6 Текущая стоимость аннуитета
Текущая стоимость аннуитета – шестая функция денег. Смысл – какова при заданной ставке дисконта текущая стоимость серии равновеликих платежей в одну денежную единицу в течение определенного периода времени.
Аннуитет – серия равновеликих платежей, вносимых через один и тот же промежуток времени, бывает обычным и авансовым.
Данная функция является обратной функции износа на амортизацию единицы. Используется для того, чтобы определить текущую стоимость регулярных платежей, получаемых в будущем в течение определенного времени.
Расчет текущей стоимости обычного аннуитета (платежи производятся в конце периода).
а) при платежах, осуществляемых один раз в конце года:
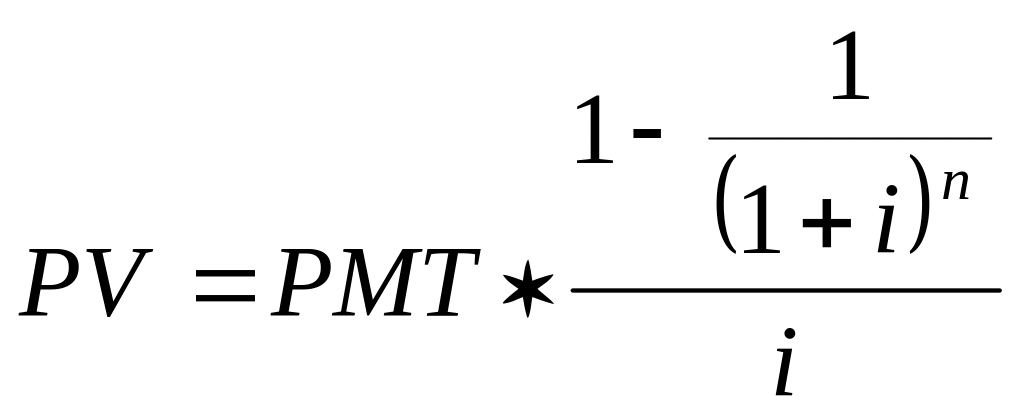(16)
б) при платежах, осуществляемых чаще, чем один раз в год в конце каждого периода:
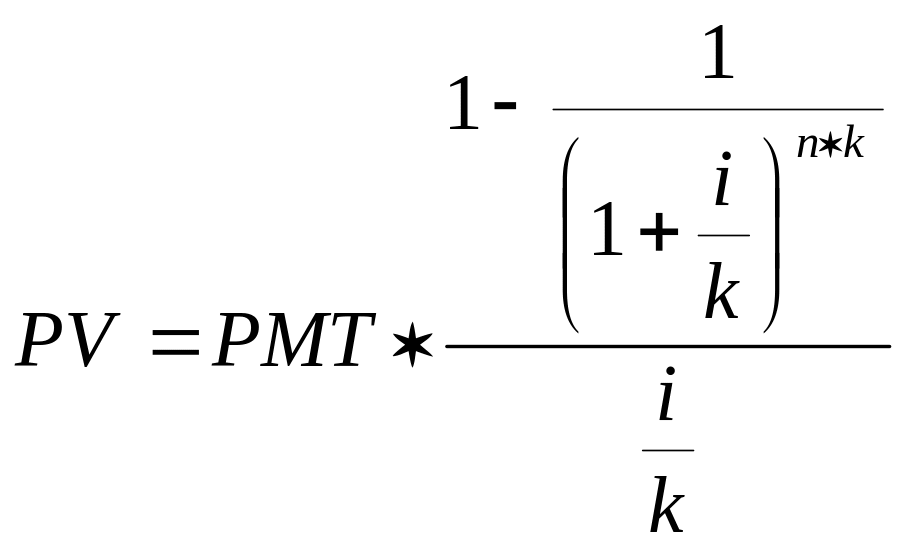(17)
Расчет текущей стоимости авансового аннуитета (платежи производятся в начале периода).
а) при платежах, осуществляемых один раз в начале года:
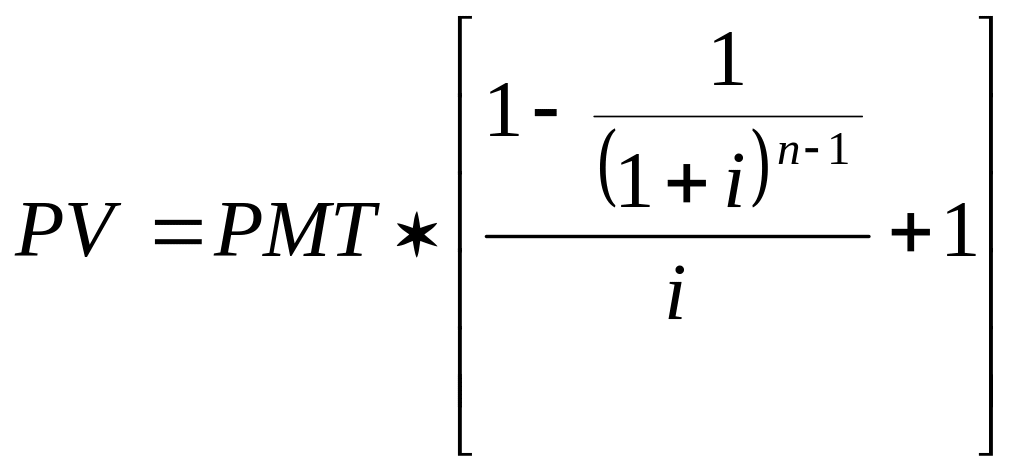(18)
б) при платежах, осуществляемых чаще, чем один раз в год, в начале каждого периода:
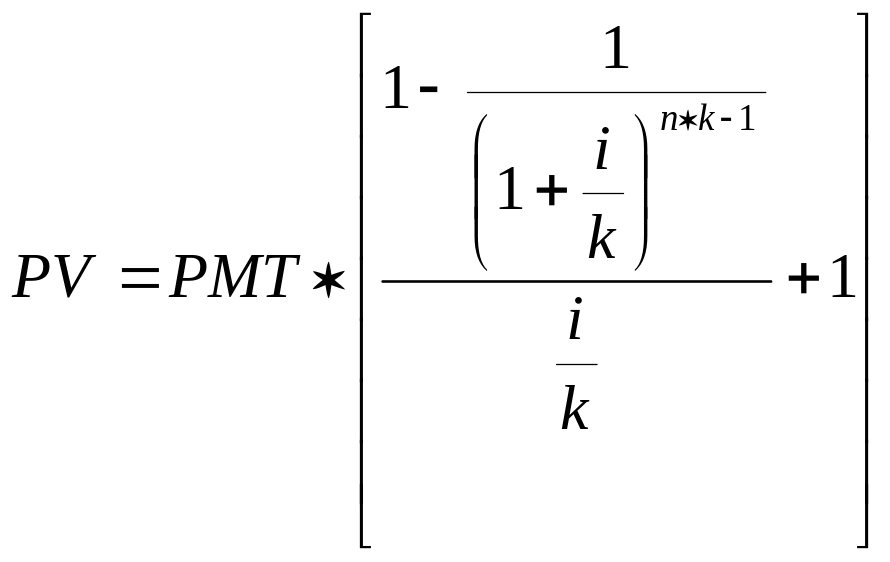(19)
Задача 6. Договор аренды квартиры составлен на 6 месяцев. Определить текущую стоимость арендных платежей при 27% ставке дисконтирования. Арендная плата выплачивается в размере 1600 рублей:
в начале каждого полугодия;
в конце каждого полугодия.
Решение:
1)
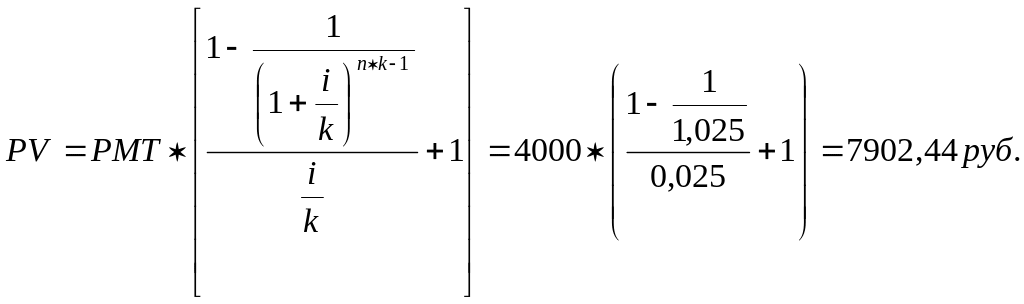
2)
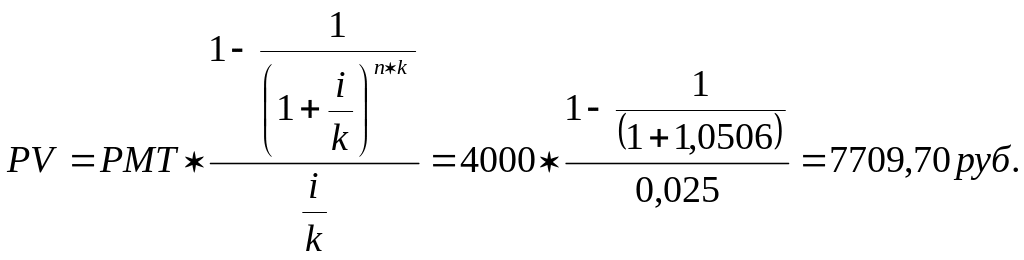
Ответ: 1) PV = 7902,44 руб.
PV = 7709,70 руб.