Приклад виконання завдання

1. Назва: ромбічна призма.

2. Формула симетрії: 3L₂3РС.

3. Кількість одиничних напрямків та їх орієнтування: три поодиноких напрямки паралельно осям L2, що проходять через центр симетрії.

Завдання

1. За моделями простих форм, виданих викладачем, визначити елементи симетрії багатогранника.

2. Записати назву простої форми.

3. Записати форму симетрії.

4. Визначити кількість одиничних напрямків та їх орієнтування.

Лабораторна робота № 2 визначення категорій та сигоній. Будування стереографічної проекції кристалу

Мета роботи - визначення категорій, сингоній та класу простих форм і будування її стереографічних проекцій.

([2], с.20-33, 41 - 44; [3], c. 21-29,42-48)

Теоретичні передумови

Перед початком роботи необхідно опрацювати теоретичні передумови в лабораторній роботі № 1.

Усе різноманіття форм кристалів розподіляється на три категорії, сім сингоній та 32 класи симетрії (табл. 1).

По кількості одиничних напрямків усі кристали поділяються на три категорії: вищу - відсутність одиничних напрямків; середню - один одиничний напрямок; нижчу - декілька одиничних напрямків.

Сингонією зветься сукупність елементів симетрії однієї категорії з однаковою кількістю осей симетрії одного і того ж порядку. Класифікація за cингоніями визначається вибором системи координат (табл. 4).

У вищій категорії є одна cингонія - кубічна. їй відповідає декартова система координат. Елементарна комірка - куб. У неї обов'язково є 4L₃.

До середньої категорії відносяться три сингонії: тригональна: а = в ≠ 0; α = β = 90°; γ = 120°. Елементарна комірка - прямокутна призма з основою у вигляді ромбу. Обов'язково має осі L₃ або L_3i;

тетрагональна;, а = в ≠ с; α = β = γ = 90°. Елементарна комірка -прямокутна призма з основою у вигляді квадрату. Обов'язково має L₄ або L_4i; гексогональна: а = в ≠ c; α = β = 90°; γ=120°. Елементарна комірка - прямокутна призма с основою у вигляді ромбу. Обов'язково має L₆ або L_6i.

До нижчої категорії належать три сингонії: ромбічна: а = в ≠ с; α = β = γ = 90°. Елементарна комірка — паралелепіпед. Обов'язково має 3L₂; моноклинна: а = в ≠ с; α = β = 90° ≠ γ. Елементарна комірка -прямокутна призма з основою у вигляді паралелограма. Має L₂ або Р, триклинна - а ≠ в ≠ с; α = β = γ. Елементарна комірка - косокутний паралелепіпед. Має тільки L₁ або С. Кількість одиничних напрямків - усі.

Класом (видом) симетрії простих тіл називають повну комбінацію елементів симетрії цього тіла. Всього існує 32 класи симетрії (табл. 1).

Більш повніше симетрія кристалу визначається за його стереографічною проекцією. Для побудови останньої навколо простого тіла описують сферу з центром, що знаходиться у центрі кристалу. За площину стереографічної проекції вибирають екваторіальну площину, на яку сфера проектується у вигляді кола проекцій. Полюс такої сфери проектується у вигляді точки у центрі кола Вертикальна вісь симетрії проектується у вигляді точки у центрі екваторіальної площини, горизонтальна - у вигляді прямої лінії, кінці якої лежать на екваторі, а похилена — у вигляді точки входу у середині проекцій:

Точки входу (виходу) осей різного порядку позначаються:

L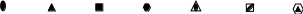 ₂ – ; L₃ – ; L₄ – ; L₆ – ; L_3i – ; L_4i – ; L_6i – .

Площина симетрії, що проходить через центр сфери та перетинає її, проектується на площину проекції у вигляді дуги великого кола. Площини симетрії позначаються подвійними лініями:

Центр симетрії, завжди проектується у центр кола проекцій та позначається маленьким колом.

Щоб не завантажувати креслення, проектують тільки перехрещення площин та осей симетрії з верхньою напівсферою. Для побудови стереографічної проекції багатогранник розміщують таким чином, щоб вісь вищого порядку була перпендикулярна до кола проекцій.