- •Лабораторна робота № 1 елементи симетрії, їх визначення. Формула симетрії
- •Теоретичні передумови
- •1. Геометрична кристалографія.
- •2. Фізична кристалографія
- •3. Хімічна кристалографія
- •Приклад виконання завдання
- •Завдання
- •Лабораторна робота № 2 визначення категорій та сигоній. Будування стереографічної проекції кристалу
- •Теоретичні передумови
- •Приклад виконання завдання
- •Завдання
- •Контрольні питання
- •Хід роботи
- •Завдання до лабораторної роботи
- •Теоретичні відомості.
- •I. Діелектричні матеріали
- •2. Поляризація діелектриків
- •3. Види поляризації діелектриків
- •4. Класифікація діелектриків по видах поляризації
- •5. Діелектричні втрати
- •6. Розрахунок потужності втрат і тангенса кута діелектричних втрат у діелектрику
- •7. Розподіл діелектриків по видах діелектричних втрат
- •Контрольні питання
- •Завдання до лабораторної роботи
- •Теоретичні відомості
- •I. Напівпровідникові матеріали
- •2. Параметри власних напівпровідників
- •3. Параметри домішкових напівпровідників
- •Контрольні питання
- •Література
Контрольні питання
Які матеріали відносяться до класу напівпровідників?
Основні характеристики напівпровідникових матеріалів?
Які фактори визначають електричну провідність напівпровідників?
Що таке власна й домішкова провідність?
Які параметри напівпровідників можна визначити з температурної залежності їхнього опору?
Чим відрізняється температурна залежність питомого опору власного напівпровідника від домішкового?
Що таке власний, донорний та акцепторний напівпровідник?
Що таке домішка заміщення та впровадження?
Як залежить рухомість носіїв заряду у власному напівпровіднику від температури?
Чим обумовлена темиературна залежність едектропровідності напівпровідника?
Які параметри характеризують домішкові напівпровідники?
Як змінюється рухомість носіїв заряду у домішкових напівпровідниках з температурою?
Як впливає температура на електропровідність домішковнх напівпровідників?
Таблиця 1
Номенклатура 32 класів (видні) симетрії кристалів
Сингонія |
Назва класів по номен- клатурі Федорівського інституту |
Формула симетрії |
Триклинна |
1. Примітивній |
L1 |
2. Центральнії |
С |
|
Моноклинна |
3. Аксіальній |
L2 |
4. Плавальний |
Р |
|
5. Планаксіальний |
L2PC |
|
Ромбічна |
6. Аксіальній |
3L2 |
7. Планальннй |
L22P |
|
8. Планаксіальний |
3L23PC |
|
Тригональна |
9. Примітивний |
L3 |
10. Центральний |
L3C = L3i |
|
11. Аксіальний |
L33L2 |
|
12. Планальний |
L33P |
|
13. План аксіальни й |
L33L23PC |
|
Тетрагональна |
14. Примітивний |
L4 |
15. Інверсіонно- |
L4i |
|
примітивний |
|
|
16. Центральний |
L4PC |
|
17. Аксіальний |
L44L2 |
|
I8. Плавальний |
L44P |
|
19.Iнверсіонно- |
L4i2L22P |
|
плавальний |
|
|
20. План аксіальни й |
L44L25PC |
|
Гексагональна |
21. Примітивний |
L6 |
22. Інверсіонно- |
L6i; L3P |
|
примітивний |
|
|
23. Центральний |
L6PC |
|
24. Аксіальний |
L66L2 |
|
25. Планальний |
L66P |
|
26.Інверсіонно- |
L6i3L23P; L33L24P |
|
планальний |
|
|
27. Планаксіальний |
L66L27PC |
|
Кубічна |
28.Примітивний |
4L33L2 |
29. Центральний |
4L33L23PC |
|
30. Аксіальний |
3L44L36L2 |
|
З1. Планальний |
4L33L26P |
|
32. Планаксіальний |
3L44L36L29PC |
Таблиця 2
Прості форми кристалів Нижча категорія
Назва |
Триклінна |
Сингонія |
|||
Моноклінна |
|||||
Моноедр |
|
|
|
|
|
Пінакоїд |
|
|
|
|
|
Діедр |
|
Осьовий (сфеноід), відкрита форма |
Площинний, (дома), закрита форма |
Осьовий (сфеноід), відкрита форма |
Р
Площинний (дома), Закрита форма |
Прості форми кристалів Нижча та середня категорії
Продовження табл.2
Назва |
Сингонія |
||||||
Ромбічна |
Тригональна |
Тетрагональна |
Гексагональна |
||||
Призми |
|
|
|
|
|
|
|
Піраміди |
|
|
|
|
|
|
|
Біпіраміди |
|
|
|
|
|
|
|
Форма поперечного перерізу |
|
|
|
|
|
|
|
Продовження табл.2
Прості форми кристалів
Нижча та середня категорії
Назва |
Сингонія |
|||||||
Ромбічна |
Тригональна |
Тетрагональна |
Гексагональна |
|||||
Трапецоедр |
|
|
лівий |
правий |
лівий |
правий |
лівий |
|
Скаленоедр (ромбоедр) |
|
ромбоедр |
тригональний скаленоедр
|
скаленоедр |
|
|||
Тетраедр |
лівий |
правий |
|
|
|
|||
Закінчення табл.2
Прості форми кристалів Вища категорія
Назва |
Кубічна сингонія |
||||||
Вихідна форма |
Ускладнені форми з числом граней |
||||||
Подвоєним |
Потроєним |
Учетвереним |
Ушестіреним |
||||
Тетраедр |
Тетраедр |
|
Тригонтри - тетраедр |
Тетрагонтри - тетраедр |
Пентагонтри- тетраедр |
|
Гексатетраедр |
Куб |
Гексаедр |
Ромбододекаедр |
|
|
Пентагон-додекаедр |
Тетрагекса-едр |
Дідодекаедр |
Октаедр |
Октаедр |
|
Тригонтри - октаедр |
Тетрагонтри - октаедр |
Пентагонтриоктаедр |
|
Гексаоктаедр |
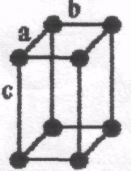
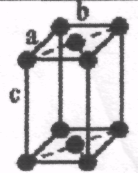
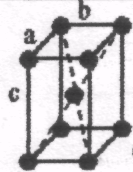
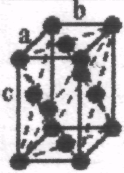
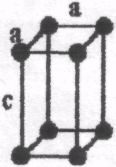
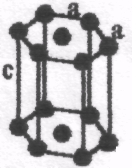
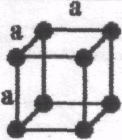
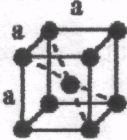
Гратки Браве
Таблиця З
|
Тип решітки |
|||
Сингонія |
Примітивна (Р) |
Базоцентрована (С) |
Об'ємно центрована (І) |
Гранецентро-вана (А, В, F) |
Триклінна |
|
|
|
|
Моноклінна |
|
|
|
|
Ромбічна |
|
|
|
|
Тригональна |
|
|
|
|
Тетрагональна |
|
|
|
|
Гексагональна |
|
|
|
|
Кубічна |
|
|
|
|
Таблиця 4
Основні характеристики категорій та сингоній
Категорія |
Сингонія |
Число одиничних нап- рямків |
Характерні елементи симетрії |
|
Нижча
Відсутні осі симетрії віще другого порядку, одиничних напрямків -більше двох. |
1. Триклінна |
Усі |
L1 або С |
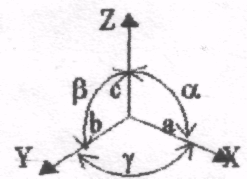
α ≠ β = γ = 90°; a ≠ b ≠ с. |
2. Моноклінна |
Безлічь |
L2 або Р |
α = β = 90° ≠ γ; a ≠ b ≠ с. |
|
3. Ромбічна |
Три |
3L2 або ЗР |
α = β = γ = 90°; a = b ≠ с. |
|
Середня
Одна вісь симетрії вище другого порядку, одиничний напрямок - один.
|
4. Тригональна |
Одне |
L3 або L3i |
α = β = 90°; γ =120°; a = b ≠ c. |
5. Тетрагональна |
Одне |
L4 або L4i |
α = β = γ = 90°; a = b ≠ с. |
|
6, Гексагональна |
Одне |
L6 або L6i |
α = β = γ = 90°; a = b ≠ с. |
|
Виша
Декілька осей симетрії вище другого порядку, одиничних напрямків -немає. |
7. Кубічна |
Немає |
4L3 |
α = β = γ = 90°; a = b = с. |



 L2
L2 P
P L2
L2





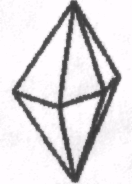
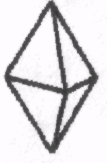

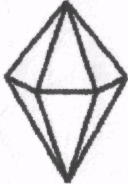






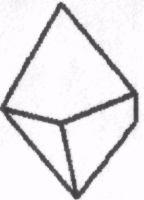
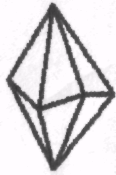
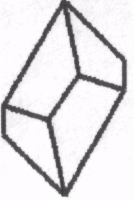
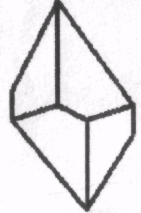
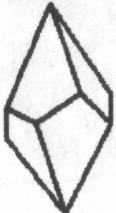
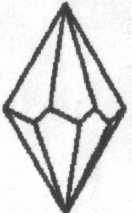
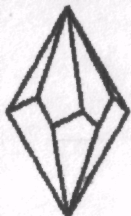
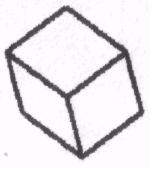

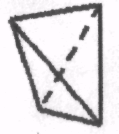

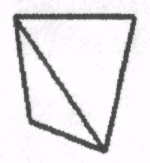
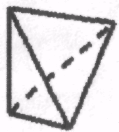
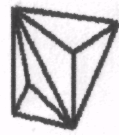
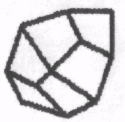
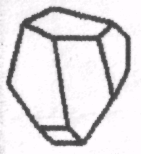

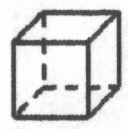
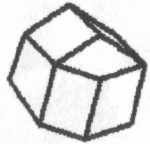
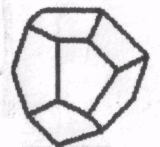





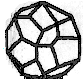

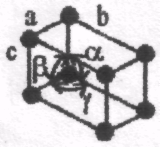 1.
1.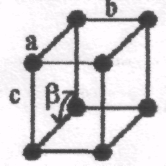 2.
2.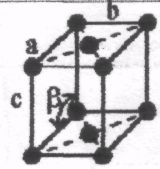 3.
3. 4.
4. 5.
5. 6.
6. 7.
7. 8.
8. 9.
9. 10.
10. 11.
11. 12.
12. 13.
13. 14.
14.