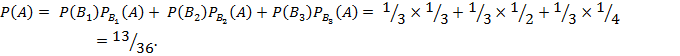1. Ймовірність подій ( сутність, властивості).

Ймовірністю події А називається кількісна оцінка можливості появи події А і позначається Р(А).

Властивості події:

1. Якщо подія А має ймовірність Р(А), то протилежна подія має ймовірність

.

2. Ймовірність неможливої події дорівнює нулю:

.

3. Ймовірність вірогідної події дорівнює одиниці:

.

4. Ймовірність випадкової події А є число, що належить сегменту [ 0 ;1]

1. Способи обчислення ймовірностей (класичний, геометричний,

статистичний).

Ми маємо або не маємо змоги провести дослід. Коли маємо – ймовірність має назву статистичної (Р * (А)) - не маємо – класичної(Р (А)).

Нехай провели n дослідів, у яких m раз відбулася подія А.Тоді статистичною ймовірністю Р *(А) події А називається відношення числа дослідів, за яких відбулась подія А, до загального числа всіх дослідів:

.

У дослідах статистична ймовірність коливається близько якогось сталого числа, змінюючись мало, причому тим менше,чим більше проведено дослідів. Якщо це число від досліду до досліду мало змінюється ,то

Класичний спосіб визначення імовірності події заснований на понятті рівноможливості чи рівновірогідності всіх можливих ісходів.

Якщо простір елементарних подій  можна подати у вигляді деякого геометричного образу, а множину елементарниx подій для події А — як частину цього геометричного образу, то ймовірність події Авизначається як відношення мір цих множин:   При цьому вважається, що ймовірність попадання в деяку частину геометричного образу пропорційна до міри цієї його частини

3.Теорема множення ймовірностей.

1] Теорема. Якщо події - несумісні,то

.

- ймовірність суми несумісних подій дорівнює сумі ймовірностей кожної події.

Наслідок. Нехай події - несумісні і одна з них вірогідна,тобто вони утворюють повну групу; тоді і .

Сума ймовірностей несумісних подій, що утворюють повну групу,дорівнює одиниці.

2] Теорема про додавання двох будь – яких ( або сумісних) подій.

- Ймовірність суми двох будь-яких подій дорівнює сумі ймовірностей кожної з них без імовірності добутку їх

5.Теорема додавання ймовірностей

Теорема. Ймовірність сумісної появи двох незалежних подій дорівнює добутку ймовірностей цих подій

Теорема. Ймовірність сумісної появи двох залежних подій дорівнює добутку ймовірності одного з них на умовну ймовірність другого

.

Події називаються незалежними в сукупності чи просто незалежними,якщо будь-яка їх комбінація незалежна.

Теорема. Ймовірність появи хоч би однієї з подій , незалежних у сукупності, дорівнює різниці між одиницею і добутком ймовірностей подій, протилежних даним.

6.Формула повної ймовірності.

Якщо В₁, В₂, …..В_n - попарно несумісні події (гіпотези), які утворюють повну групу подій, та А – випадкова подія, яка може відбутися лише при появі одного з В_i, то ймовірність події А дорівнює сумі добутків ймовірностей кожної з гіпотез на відповідну умовну ймовірність події А

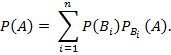
Приклад. У гаражі С групуються машини для забору вантажів з місць, позначених на рисунку точками. Машини в рівних кількостях відправляються за вантажом по магістралях . Машина з фіксованим номером може потрапити на кожну з цих магістралей. Яка ймовірність того, що саме ця машина потрапить до місця .

Розв‘язок. Висунемо гіпотези:

– « машина потрапила на магістраль » ;

– « машина потрапила на магістраль » ;

– « машина потрапила на магістраль » ;

За формулою повної ймовірності одержуємо