Кинематический анализ кулачкового механизма

Кинематический анализ кулачкового механизма может быть проведен любым из описанных выше методов. При исследовании кулачковых механизмов с типовым законом движения выходного звена наиболее часто применяется метод кинематических диаграмм. Для применения этого метода необходимо определить одну из кинематических диаграмм. Так как при кинематическом анализе кулачковый механизм задан, то известна его кинематическая схема и форма конструктивного профиля кулачка. Построение диаграммы перемещений проводится в следующей последовательности (для механизма с внеосным поступательно движущимся толкателем):

• строится, касательно к конструктивному профилю кулачка, семейство окружностей с радиусом, равным радиусу ролика; соединяются центры окружностей этого семейства плавной кривой и получается центровой или теоретический профиль кулачка

• в полученный центровой профиль вписываются окружности радиусов r0 и r0 +hAmax,определяется величина эксцентриситета е

• по величине участков, не совпадающих с дугами окружностей радиусов r0 и r0 +hAmax , определяются фазовые углы раб , у ,  дв и с

• дуга окружности r, соответствующая рабочему фазовому углу, разбивается на несколько дискретных участков; через точки разбиения проводятся касательно к окружности радиуса эксцентриситета прямые линии (эти линии соответствуют положениям оси толкателя в его движении относительно кулачка)

• на этих прямых измеряются отрезки расположенные между центровым профилем и окружностью радиуса r₀ ; эти отрезки соответствуют перемещениям центра ролика толкателя SВi по полученным перемещениям SВiстроится диаграмма функции положения центра ролика толкателя SВi= f(1)

Рис.17.4

На рис. 17.4 показана схема построения функции положения для кулачкового механизма с центральным (е=0) поступательно движущимся роликовым толкателем.

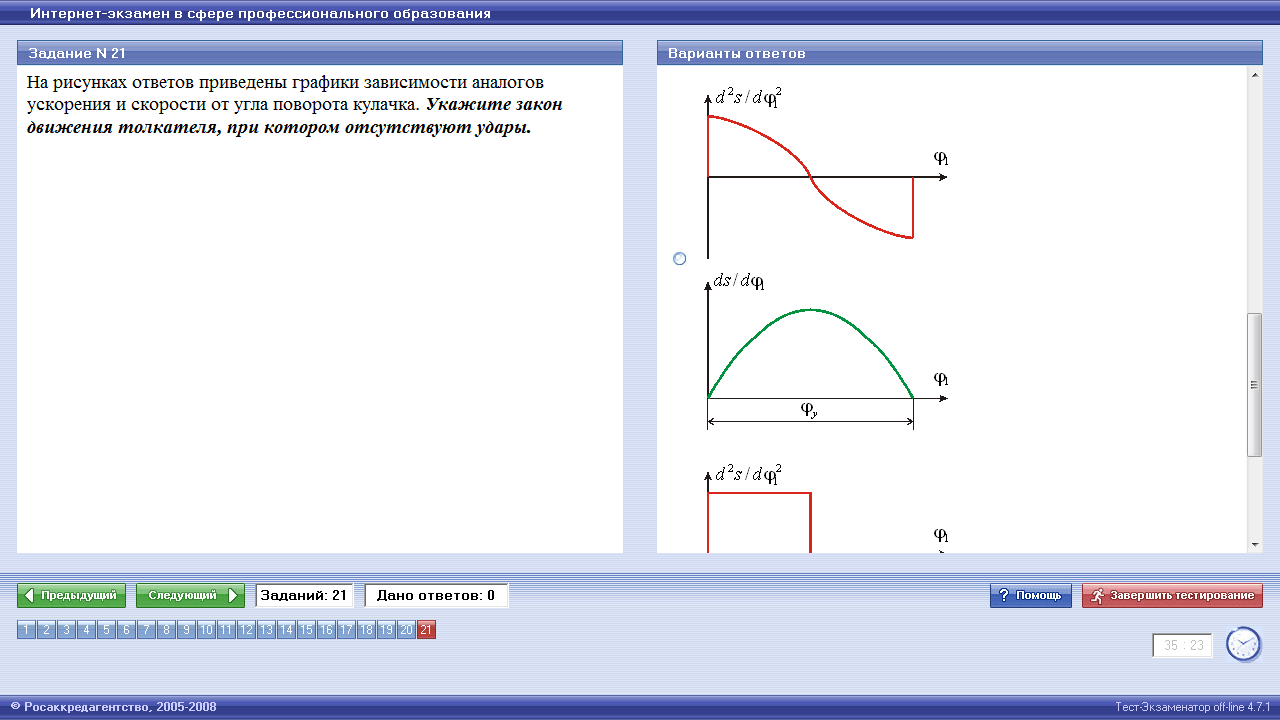
Типовые законы движения толкателя.

При проектировании кулачковых механизмов выбирается закон движения толкателя из набора типовых.

Типовые законы движения делятся на законы с жесткими и мягкими ударами и законы безударные. С точки зрения динамических нагрузок, желательны безударные законы. Однако кулачки с такими законами движения технологически более сложны, так как требуют более точного и сложного оборудования, поэтому из изготовление существенно дороже. Законы с жесткими ударами имеют весьма ограниченное применение и используются в неответственных механизмах при низких скоростях движения и невысокой долговечности. Кулачки с безударными законами целесообразно применять в механизмах с высокими скоростями движения при жестких требованиях к точности и долговечности. Наибольшее распространение получили законы движения с мягкими ударами, с помощью которых можно обеспечить рациональное сочетание стоимости изготовления и эксплуатационных характеристик механизма.

После выбора вида закона движения, обычно методом кинематических диаграмм, проводят геометро-кинематическое исследование механизма и определяют закон перемещения толкателя и закон изменения за цикл первой передаточной функции (см. лекцию 3 - метод кинематических диаграмм).

Таблица 17.1

№ п.п.	Типовой закон движения	Параметры  закона движения
1.	Линейный	с жесткими ударами при 1= 0  aqB= при 1= ур при 1= у
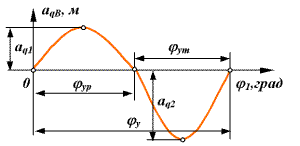
2.	параболический	с мягкими ударами aq1aq2; урур;  aq1ур = aq2ут или aq1 = aq2;  ур = ур;  aq1ур = aq2ут
3.	косинусоидальный	с мягкими ударами aq1 aq2; ур ут;  aq3 aq4 ;  (aq1+aq2)ур =  =(aq3+aq4)ут
4.	полинома	с мягкими ударами aq1 aq2; урут;  0.5 aq1ур= 0.5 aq2ут
5.	полинома	безударный aq1 aq2; урут;  0.5 aq1ур= 0.5 aq2ут
6.	Синусоидальный	безударный aq1  aq2; урут ;

Критерии работоспособности и угол давления при передаче движения в высшей кинематической паре.

Угол давления определяет положение нормали п-п в высшей КП относительно вектора скорости и контактной точки ведомого звена (рис. 3, а, б). Его величина определяется размерами механизма, передаточной функцией и перемещения толкателя S_.

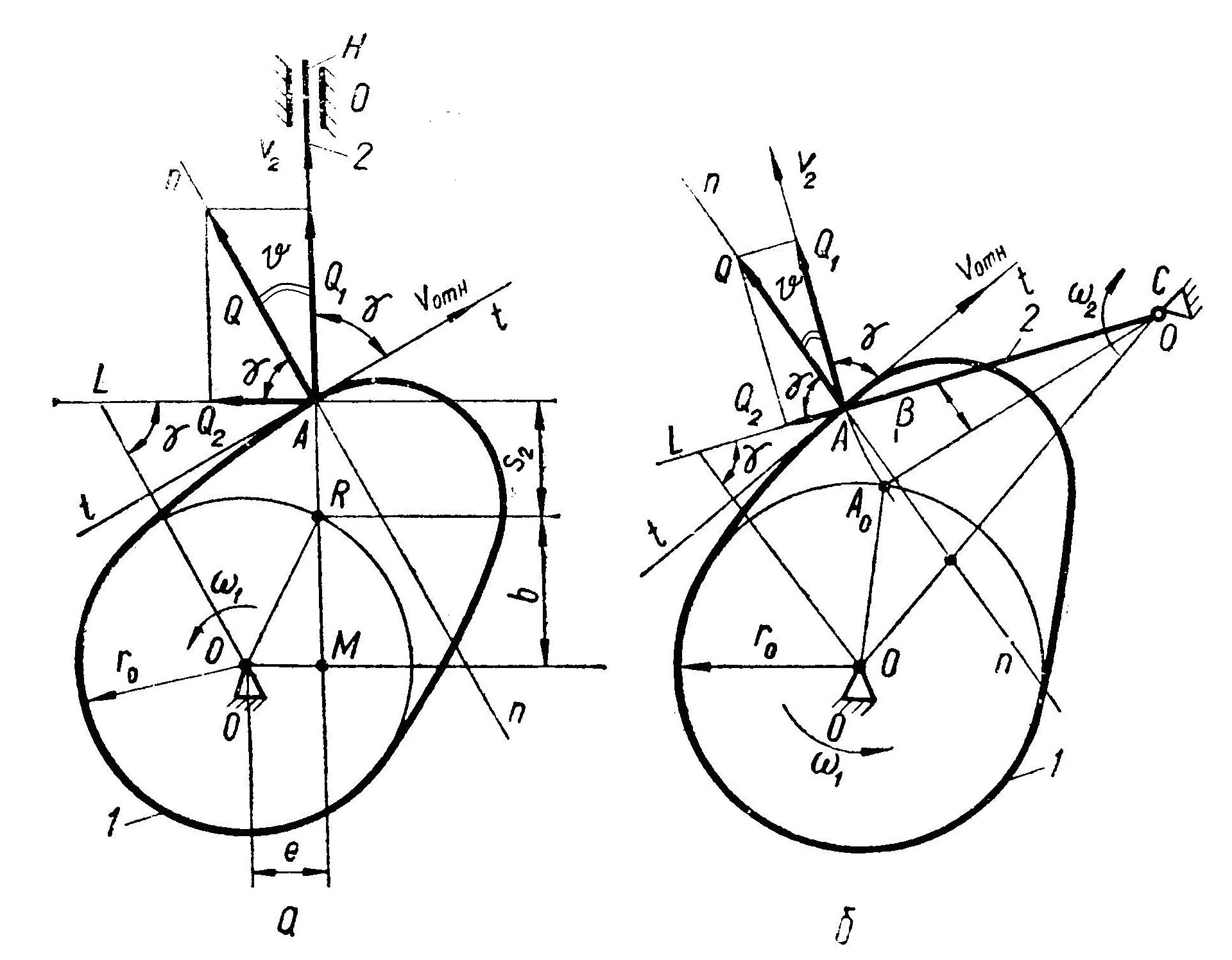
Угол передачи движения γ - угол между векторами υ₂ и υ_отн абсолютной и относительной (по отношению к кулачку) скоростей той точки толкателя, которая находится в точке контакта А (рис. 3, а, б):

.

Если пренебречь силой трения между кулачком и толкателем, то силой, приводящей в движение толкатель (движущей силой), является давление Q кулач­ка, приложенное к толкателю в точке А и направленное по общей нор­мали п-п к профилям кулачка и толкателя. Разложим силу Q на взаимно перпендикулярные составляющие Q₁ и Q₂, из которых первая направ­лена по направлению скорости υ₂. Сила Q₁ перемещает толкатель, преодолевая при этом все полезные (связанные с выполнением технологических задач) и вредные (силы тре­ния) сопротивления, приложенные к толкателю. Сила Q₂ увеличива­ет силы трения в кинематической паре, образованной толкателем и стойкой.

Очевидно, что с уменьшением угла γ сила Q₁ уменьшается, а сила Q₂ увеличивается. При некотором значении угла γ может оказаться, что сила Q₁ не сможет преодолеть все сопротивле­ния, приложенные к толкателю, и механизм не будет работать. Такое явление называют заклиниванием механизма, а угол γ, при котором оно имеет место, называют углом заклинивания γ_закл .

При проектировании кулачкового механизма задают допускаемое значение угла давления _доп , обеспечивающее выполнения условия γ ≥ γ _min > γ _закл , т. е. текущий угол γ ни в одном положении ку­лачкового механизма не должен быть меньше минимального угла передачи γ _min и значительно превосходить угол заклинивания γ_закл .

Для кулачковых механизмов с поступательно движущимся толкателем рекомендуется γ _min = 60° (рис. 3, а) и γ_min = 45° - механизмов с вращающимся толкателем (рис. 3, б).