2 Время сложной реакции

Для определения оптимальной величины интервала h используют формулу Стерджеса:

h = ,

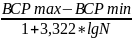где ВСР_max, ВСР_min-максимальное и минимальное значение времени простой реакции в исследуемом вариационном ряду, с.;

N- общее число наблюдений. N=29.

h = =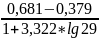 =0,052 с.

h = 0.05 c.

V_ср = 0,507 сек ;

Построение интервального вариационного ряда.

Таблица 3

Границы интервалов, с.	Середины интервалов Vci, с.	Опытные частоты, mi*	Опытные частости, Pi*	Накопленные частости, F(v)	mi* *Vci,	mi* *V2ci,	(Vci, - Vср)3 * Pi*	(Vci, - Vср)4 * Pi*
0,355-0,405	0,38	3	0,103	0,103	1,14	0,433	-0,00021		0,000027
0,405-0,455	0,43	5	0,172	0,275	2,15	0,925	-0,000079		0,0000061
0,455-0,505	0,48	8	0,276	0,551	3,84	1,843	-0,000005		0,00000013
0,505-0,555	0,53	7	0,241	0,792	3,71	1,966	0,000003		0,00000007
0,555-0,605	0,58	3	0,103	0,896	1,74	1,009	0,00004		0,000003
0,605-0,655	0,63	0	0	0,896	0	0	0		0
0,655-0,705	0,68	3	0,103	1,0	1,74	1,183	0,00053		0,000092
Сумма	-	29	1	-	14,32	7,359	0,000279		0,000128

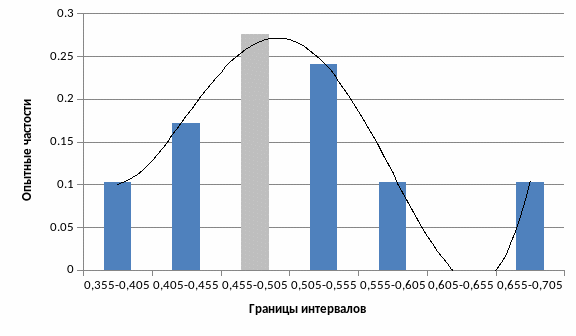
Рисунок 2 - Интервалы ВСР

Красным цветом обозначен интервал, в который входит значение ВСР студента.

Из графика видно, что данное распределение близко к нормальному.

Рассчитаем статистические параметры:

Математическое ожидание:

=

_вср = = 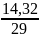= 0,49 сек;

Статическая дисперсия:

(V) = - ;

(V)_вср= - =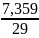 - 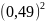= 0,014;

Несмещенная оценка дисперсии:

D(V) = * (V)_вср;

D(V)_вср = *0,014 = 0,0145;

Стандартное среднеквадратическое отклонение:

= ;

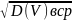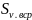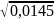= = 0,12 сек;

Коэффициент вариации:

ν= *100% ;

ν_вср= 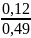* 100% =24,5%;

В данном случае коэффициент вариации менее 33%, следовательно это говорит об однородности информации.

Ассиметрия:

= ∑ * ;

A_sвср = *0,000279= 0,16 ;

В данном случае видно, что распределение правосторонее.

Эксцесс:

EK= *Pi – 3 ;

EK_вср = 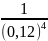* 0,000128– 3 = -2,38 ;

Данный график распределения имеет более плоскую вершину.

3 Время сложной реакции с помехой

Для определения оптимальной величины интервала h используют формулу Стерджеса:

h = ,

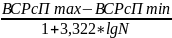где ВСРсП_max, ВСРсП_min-максимальное и минимальное значение времени простой реакции в исследуемом вариационном ряду, с.;

N- общее число наблюдений. N=29.

h = = =0,077 с.

h = 0,075 c.

V_ср = 0,481 сек ;

Построение интервального вариационного ряда.

Таблица 4

Границы интервалов, с.	Середины интервалов Vci, с.	Опытные частоты, mi*	Опытные частости, Pi*	Накопленные частости, F(v)	mi* *Vci,	mi* *V2ci,	(Vci, - Vср)3 * Pi*	(Vci, - Vср)4 * Pi*
0,165-0,24	0,2025	1	0,034	0,034	0,2025	0,041	-0,00073		0,000071
0,24-0,315	0,2775	0	0	0,034	0	0	0		0
0,315-0,39	0,3525	3	0,103	0,137	1,06	0,374	-0,00022		0,000028
0,39-0,465	0,4275	6	0,207	0,345	2,57	1,099	-0,000032		0,0000017
0,465-0,54	0,5025	13	0,448	0,794	6,53	3,281	0,0000045		0,0000001
0,54-0,615	0,5775	3	0,103	0,896	1,73	0,999	0,000093		0,000009
0,615-0,69	0,6525	3	0,103	1,0	1,96	1,279	0,00052		0,000089
Сумма	-	29	1	-	14,05	7,073	-0,000465		0,000199

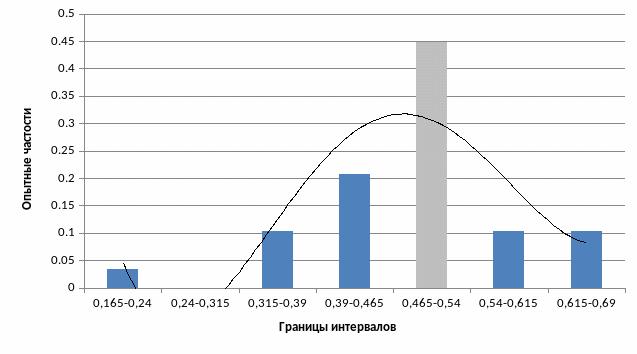
Рисунок 3 - Интервалы ВСРсП

Красным цветом обозначен интервал, в который входит значение ВСРсП студента.

Из графика видно, что данное распределение близко к нормальному.

Рассчитаем статистические параметры:

Математическое ожидание:

=

_всрсп = = 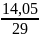= 0,48 сек;

Статическая дисперсия:

(V) = - ;

(V)_всрсп= - =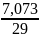 - 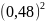= 0,013;

Несмещенная оценка дисперсии:

D(V) = * (V)_всрсп;

D(V)_всрсп = *0,013 = 0,0135;

Стандартное среднеквадратическое отклонение:

= ;

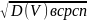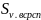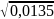= = 0,12 сек;

Коэффициент вариации:

ν= *100% ;

ν_всрсп= * 100% =24,2%;

В данном случае коэффициент вариации менее 33%, следовательно это говорит об однородности информации.

Ассиметрия:

= ∑ * ;

A_sвсрсп = *(-0,000465)= -0,27 ;

В данном случае видно, что распределение левосторонее.

Эксцесс:

EK= *Pi – 3 ;

EK_всрсп = * 0,000199– 3 = -2,04 ;

Данный график распределения имеет более плоскую вершину.