Задание 2

Согласно выданному варианту и, используя соотношения y³, y⁴, …, y¹⁴, построить и отформатировать графики функций принадлежности, приведенных ниже.

при a = 2, d₁ = 4, d₂ = 10, d₃ = 16, b = 20.

при a = 2, d₁ = 4, d₂ = 10, d₃ = 16, b = 20.

п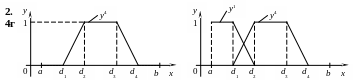 ри a = 2, d₁ = 4, d₂ = 10, d₃ = 16, b' = 20, d₄ = 22, b" = 26.

при a = 2, d₁ = 4, d₂ = 10, d₃ = 16, d₄ = 20, b = 24.

при a = 2, d₁ = 4, d₂ = 10, d₃ = 16, d₄ = 20, b = 24.

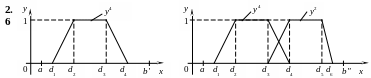
при a = 2, d₁ = 4, d₂ = 10, d₃ = 14, d₄ = 18, b' = 22, d₅ = 24, d₆ = 28, b" = 30.

при a = 2, d₁ = 4, d₂ = 10, d₃ = 16, b = 18.

при a = 2, d₁ = 4, d₂ = 10, d₃ = 16, b = 18.

при a = 2, d₁ = 4, d₂ = 10, d₃ = 16, b' = 18, d₄ =22, b" = 24.

при a = 1, d₁ = 2, d₂ = 4, d₃ = 6, d₄ = 8, d₅ = 10, d₆ = 12, b = 14.

при a = 1, d₁ = 2, d₂ = 4, d₃ = 6, d₄ = 8, d₅ = 10, d₆ = 12, b = 14.

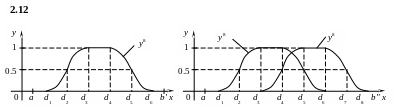
при a = 1, d₁ = 2, d₂ = 4, d₃ = 6, d₄ = 8, d₅ = 10, d₆ = 12, b' = 14, d₇ = 14, d₈ = 16,

b" = 18.

при d₁ = 4.5, d₂ = 5, d₃ = 5.5, Δd = 0.5, а = 3.

п ри d₁ = 4.5, d₂ = 5, d₃ = 5.5, Δd = 0.5, b = 8

при d₁ = 4.5, d₂ = 5, d₃ = 5.5 , d₄ = 5.3, d₅ = 5.8, , d₆ = 6.3, Δd = 0.5.

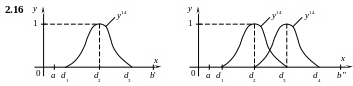
при a = 2, d₁ = 4, d₂ = 10, d₃ = 16, b' = 20, d₄ =22, b" = 26.

1.4.2.Трехмерные графики функций

1.5. Символьные вычисления

Для выполнения символьных вычислений предназначен Symbolic Math Toolbox. Ниже приводятся примеры выполнения символьных вычислений.

1.5.1. Классический метод решения дифференциальных уравнений

Классический метод решения будем применять к неоднородному линейному дифференциальному уравнению

,

приведенному к виду

путем деления на a₂ левой и правой части исходного дифференциального уравнения. Тогда a = a₀/a₂; b = a₀/a₂; с = b₀/a₂. Рассмотрим пример решения приведенного неоднородного дифференциального уравнения, у которого корни характеристического уравнения являются отрицательными и действительными.

Пример 1.5.1. Найти решение неоднородного линейного дифференциального уравнения

(1.2)

при нулевых начальных условиях y(0) = 0, (0) = 0 и единичном ступенчатом входном сигнале u(t) = 1(t).

Решение. Решение неоднородного дифференциального уравнения всегда равно сумме y(t) = y_о(t) + y_ч(t), где y_о(t) – общее решение соответствующего однородного дифференциального уравнения, полученного приравниванием нулю правой части (1.2)

, (1.3)

а y_ч(t) – частное решение, определяемое видом правой части (1.2). Решение однородного дифференциального уравнения (1.3) начинается с задания соответствующего характеристического уравнения

p² + 8p + 12 = 0

и определения его корней

p_1,2 = –4 ± ,

p₁ = – 4 + 2 = –2; p₂ = – 4 – 2 = – 6.

Общее решение однородного дифференциального уравнения запишется так

,

где С₁, С₂ – постоянные интегрирования.

Перейдем к определению частного решения y_ч. Правая часть уравнения (1.2) – константа. Частное решение ищется в форме y_ч = B, где B – константа. Для нахождения B подставим y_ч = B в уравнение (1.2)

12B = 48, B = 4.

Таким образом, полное решение неоднородного уравнения (1.2) имеет вид

. (1.4)

Исходя из нулевых начальных условий y(0) = 0, (0) = 0, запишем (1.4) в виде двух уравнений

y(0) = С₁ + С₂ + 4 = 0,

(0) = –2С₁ – 6С₂ = 0

и решим их относительно С₁ и С₂

С₁ = – 6, С₂ = 2.

Подставляя найденные значения С₁ и С₂ в (1.4), получим искомое решение

. (1.5)

Найдите в MATLAB и сравните с (1.5) решение неоднородного дифференциального уравнения, используя оператор dsolve. Наберите программу решения дифференциального уравнения (1.2) с нулевыми начальными условиями.

>> y=dsolve('D2y+8*Dy+12*y=48','y(0)=0','Dy(0)=0')

y = 2*exp(-6*t)-6*exp(-2*t)+4

Последнее выражение и будет решением линейного неоднородного дифференциального уравнения (1.2).

Постройте график переходного процесса при u(t) = 1(t) по программе

>> t = 0:0.1:10;

>> y = 2*exp(-6*t)-6*exp(-2*t)+4;

>> plot(t,y,'k'), grid on