4.33 Определить реакции опор a, b, c и шарнира d составной балки, изображенной на рисунке вместе с нагрузкой.

4.34 Определить реакции опор a, b, c и шарнира d составной балки, изображенной на рисунке вместе с нагрузкой.

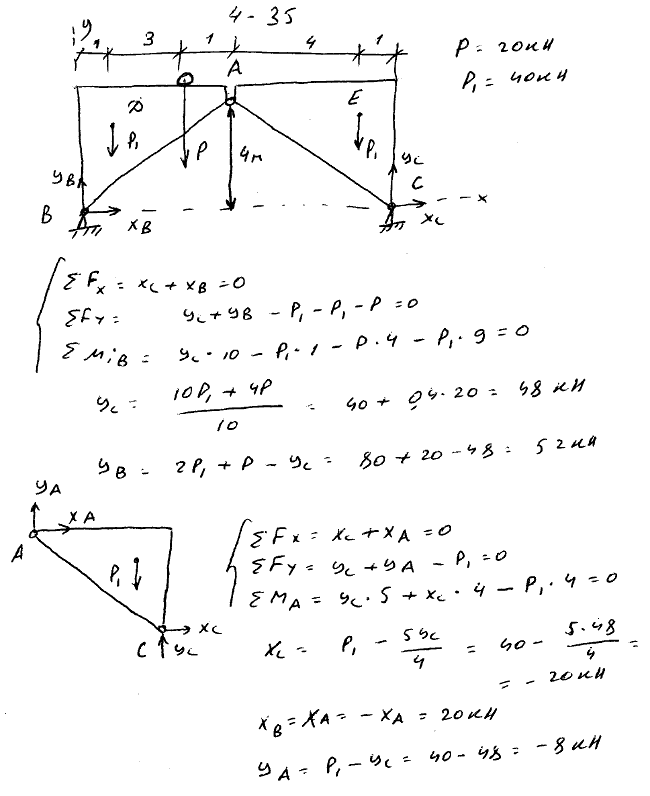
4.35 Мост состоит из двух частей, связанных между собой шарниром A и прикрепленных к береговым устоям шарнирами B и C. Вес каждой части моста 40 кН; их центры тяжести D и E; на мосту находится груз P=20 кН; размеры указаны на рисунке. Определить силу давления в шарнире A и реакции в точках B и C.

4.36 На гладкой горизонтальной плоскости стоит передвижная лестница, состоящая из двух частей AC и BC, длины 3 м, веса 120 Н каждая, соединенных шарниром C и веревкой EF; расстояние BF=AE=1 м; центр тяжести каждой из частей AC и BC находится в ее середине. В точке D на расстоянии CD=0,6 м стоит человек, весящий 720 Н. Определить реакции пола и шарнира, а также натяжение T веревки EF, если угол BAC=ABC=45°.

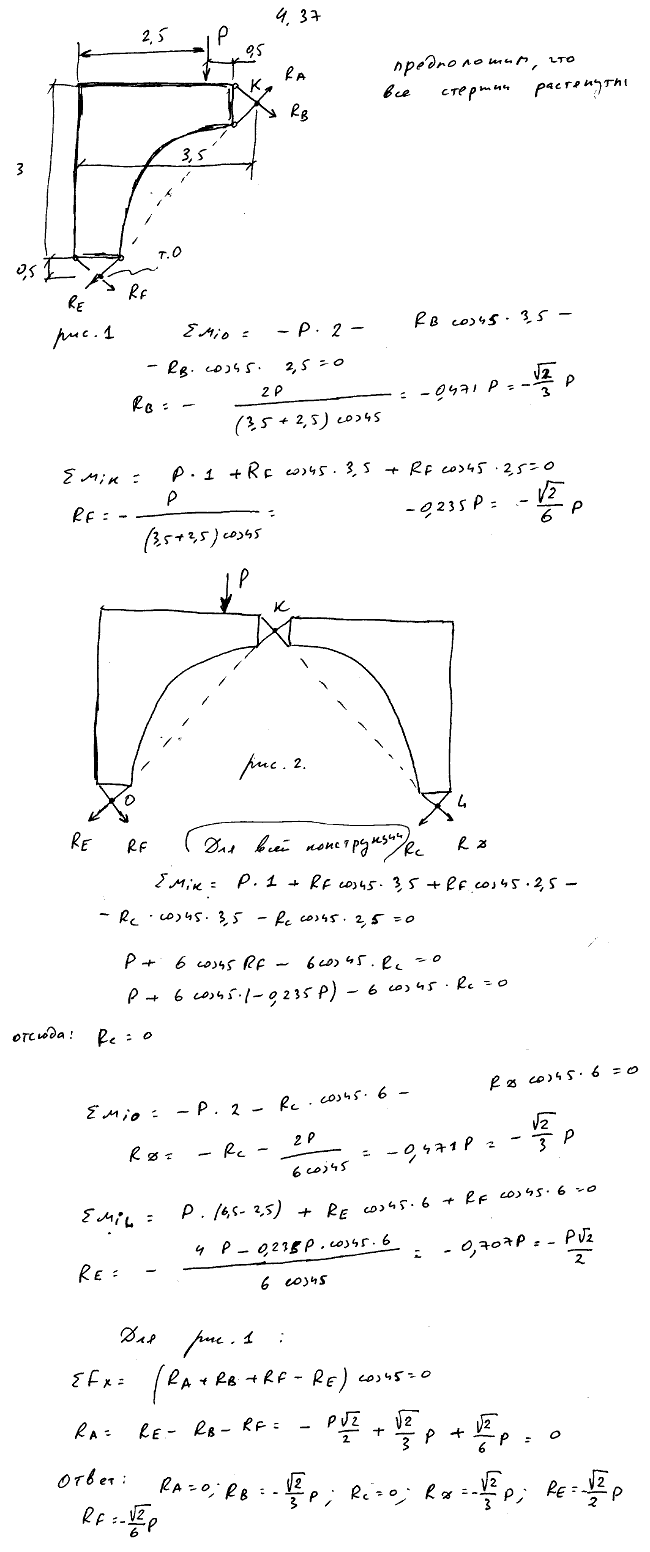
4.37 Мост состоит из двух одинаковых частей M и N, соединенных между собой и с неподвижными опорами посредством шести стержней, наклоненных к горизонту под углом 45° и снабженных на концах шарнирами. Размеры указаны на рисунке. В точке G помещен груз веса P. Определить те усилия в стержнях, которые вызваны действием этого груза.

4.38 Мост состоит из двух одинаковых горизонтальных балок, соединенных шарниром A и прикрепленных шарнирно к основанию жесткими стержнями 1, 2, 3, 4, причем крайние стержни вертикальны, а средние наклонены к горизонту под углом α=60°. Соответствующие размеры равны: BC=6 м; AB=8 м. Определить усилия в стержнях и реакцию шарнира A, если мост несет вертикальную нагрузку P=15 кН на расстоянии a=4 м от точки B.

4.39 Вдоль мастерской, здание которой поддерживается трехшарнирной аркой, ходит по рельсам мостовой кран. Вес поперечной балки, передвигающейся по рельсам, 12 кН; вес крана 8 кН (кран не нагружен); линия действия веса крана отстоит от левого рельса на расстоянии 0,25 длины балки. Вес каждой половины арки равен 60 кН и приложен на расстоянии 2 м от вертикали, проходящей через соответствующую опору A или B; опорные рельсы мостового крана расположены на расстоянии 1,8 м от этих вертикалей. Высота здания 12 м, ширина пролета 16 м. Равнодействующая сил давления ветра равна 12 кН и направлена параллельно AB, линия ее действия отстоит от AB на 5 м. Определить реакции шарниров A и B и силу давления в шарнире C.

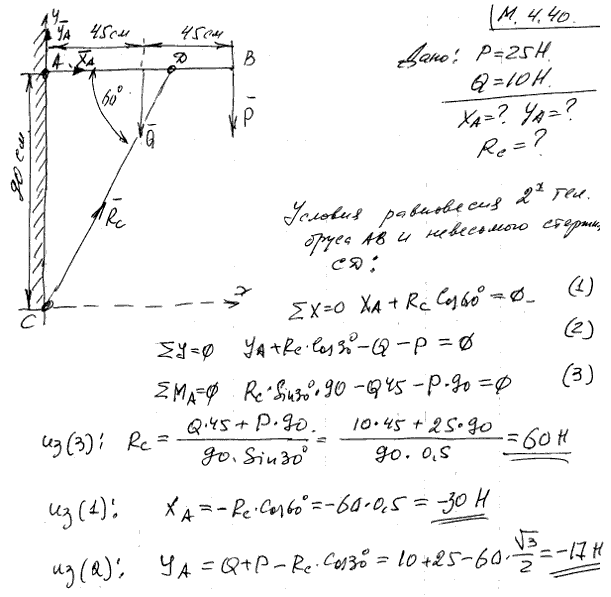
4.40 Груз P=25 Н подвешен к концу горизонтального бруса AB. Вес бруса Q=10 Н и приложен в точке E. Брус прикреплен к стенке посредством шарнира A и подперт стержнем CD, с которым скреплен тоже посредством шарнира. Весом стержня CD пренебрегаем. Размеры указаны на рисунке. Определить реакции шарниров A и C.

4.41 Два однородных бруса одинаковой длины соединены шанирно в точке C, а в точках A и B также шарнирно прикреплены к опорам. Вес каждого бруса равен P. В точке C подвешен груз Q. Расстояние AB=d. Расстояние точки С до горизонтальной прямой AB равно b. Определить реакции шарниров A и B.

4.42 Два стержня AC и BD одинаковой длины шарнирно соединены в точке D и так же прикреплены к вертикальной стене в точках A и B. Стержень AC расположен горизонтально, стержень BD образует угол 60° с вертикальной стеной. Стержень AC в точке E нагружен вертикальной силой P1=40 Н и в точке C силой Q=100 Н, наклоненной к горизонту под углом 45°. Стержень BD в точке F нагружен вертикальной силой P2=40 Н. Дано: AE=EC, BF=FD. Определить реакции шарниров A и B.

4.43 Подвеска состоит из двух балок AB и CD, соединенных шарнирно в точке D и прикрепленных к потолку шарнирами A и C. Вес балки AB равен 60 Н и приложен в точке E. Вес балки CD равен 50 Н и приложен в точке F. В точке B к балке AB приложена вертикальная сила P=200 Н. Определить реакции в шарнирах A и C, если заданы следующие размеры: AB=1 м; CD=0,8 м; AE=0,4 м; CF=0,4 м; углы наклона балок AB и CD к горизонту соответственно равны: α=60° и β=45°.

4.44 Горизонтальная балка AB длины 2 м, прикрепленная к вертикальному столбу AC в точке A и подпертая подкосом DE, несет на конце груз Q веса 500 Н; столб AC укреплен подкосом FG, причем AE=CG=1 м; подкосы DE и FG наклонены под углом 45° к горизонту. Найти усилия SE и SF в подкосах DE и FG и реакцию грунта в точке C, предполагая, что крепления шарнирные, и пренебрегая весом балки, столба и подкосов.

4.45 В мостовой ферме, изображенной на рисунке, на узлы C и D приходится одинаковая вертикальная нагрузка P=100 кН; наклонные стержни составляют углы 45° с горизонтом. Найти усилия в стержнях 1, 2, 3, 4, 5 и 6, вызываемые данной нагрузкой.

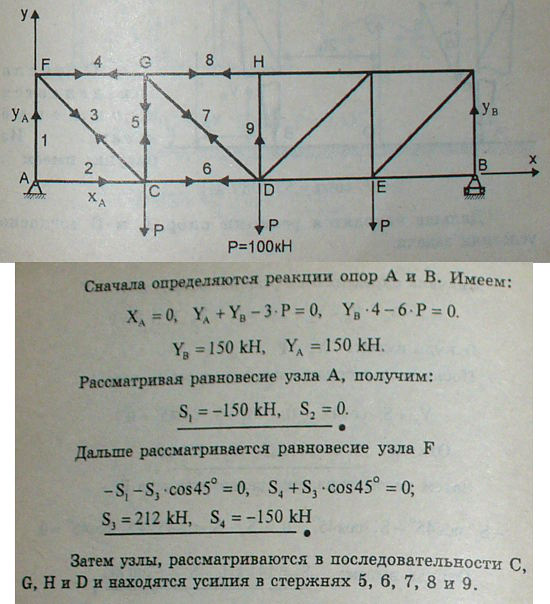
4.46 В мостовой ферме, изображенной на рисунке, узлы C, D и E загружены одинаковой вертикальной нагрузкой P=100 кН. Наклонные стержни составляют углы 45° с горизонтом. Найти усилия в стержнях 1, 2, 3, 4, 5, 6, 7, 8 и 9, вызываемые данной нагрузкой.

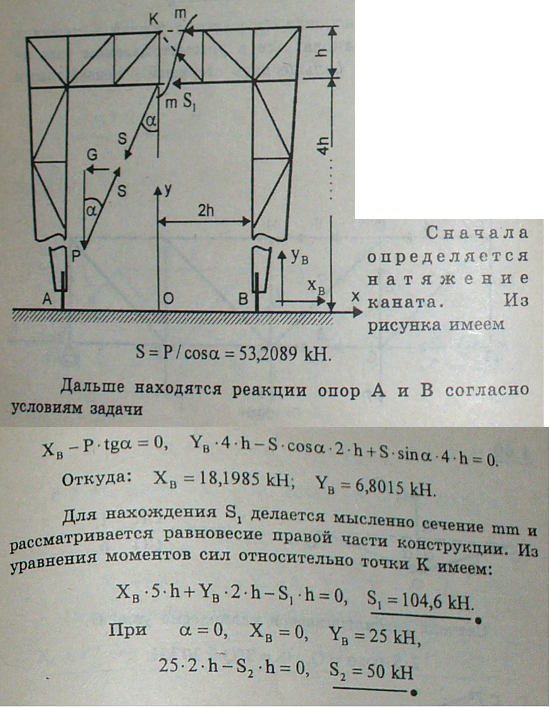
4.47 Для сборки моста устроен временный деревянный кран, перемещающийся по рельсам A и B на колесах. К среднему узлу C нижнего пояса DE крана прикреплен блок, служащий для поднятия тяжести с помощью цепи. Вес поднимаемого с подмостей груза P=50 кН, причем в момент отделения его от подмостей направление цепи составляет с вертикалью угол α=20°; во избежание колебаний груза он оттягивается горизонтальным канатом GH.

Предполагая, что горизонтальная составляющая натяжения цепи воспринимается одним правым рельсом B, определить усилие S1 в горизонтальном стержне CF в момент отделения груза от подмостей и сравнить его с тем усилием S2, которое получилось бы при угле α=0. Размеры указаны на рисунке.

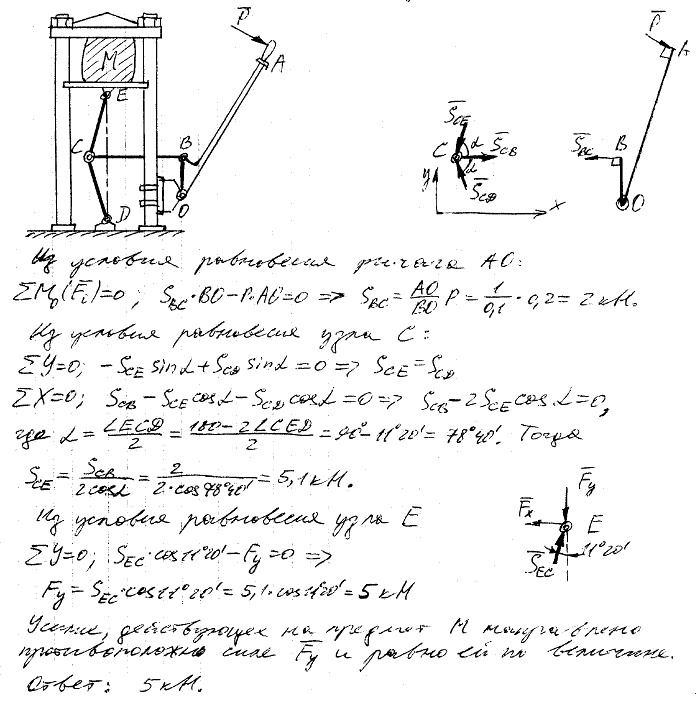
4.48 Найти величину усилия, сжимающего предмет M в прессе, при следующих условиях: усилие P=0,2 кН и направлено перпендикулярно рычагу OA, имеющему неподвижную ось O; в рассматриваемом положении пресса тяж BC перпендикулярен OB и делит ∠ECD пополам, причем ∠CED=arctg 0,2=11°20'; длина OA=1 м; OB=10 см.

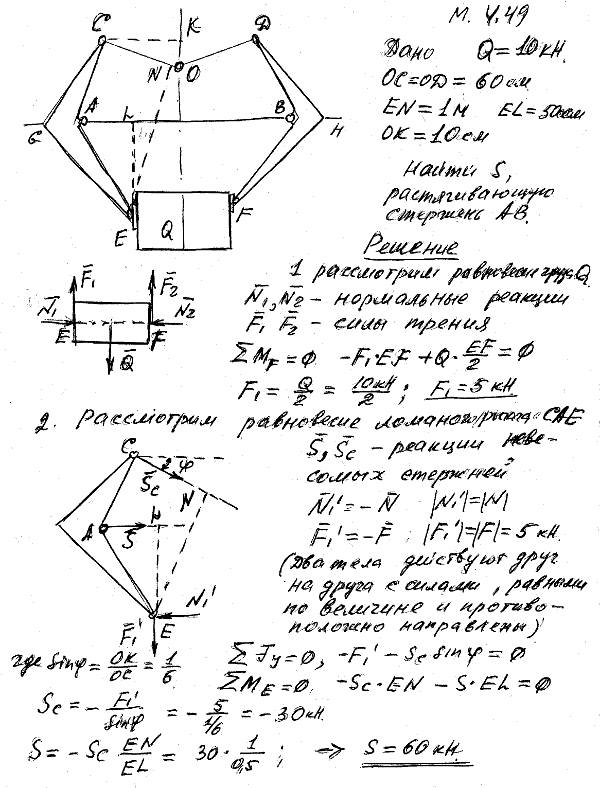
4.49 Цепь OO1 самозахватывающего грузы приспособления соединена шарниром O со стержнями OC=OD=60 см. Стержни соединены шарнирами же с двумя равными ломаными рычагами CAE и DBF, которые могут вращаться вокруг точек A и B соединительного стержня GH. В шарнирах E и F особые колодки удерживают груз Q=10 кН трением. Расстояние точки E от стержня GH равно EL=50 см, а расстояние ее от стержня OC равно EN=1 м. Высота треугольника COD равна OK=10 см. Найти силу, растягивающую соединительный стержень GH, пренебрегая весом частей механизма.

4.50 Определить реакции шарниров A, C, D, E и H в стержневой системе, изображенной на рисунке, если CE=EH=HD и AC=CB.

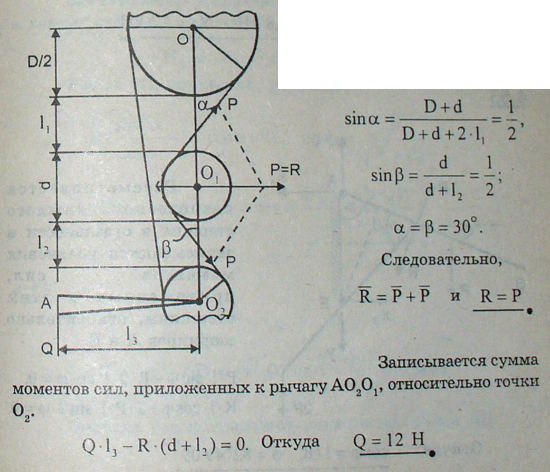
4.51 Натяжение приводного ремня, осуществляемое при помощи ломаного рычага AO2O1 и натяжного ролика O1, равно по ту и другую сторону ролика P Н. Найти величину груза Q при равновесии системы, если дано: ∠AO2O1=90°, D=55 см, d=15 см, l1=35 см, l2=15 см, l3=45 см, P=18 Н.

4.52 Груз P веса 4,8 кН удерживается на гладкой наклонной плоскости посредством веревки, параллельной плоскости и намотанной на неподвижный вал лебедки ABC. Угол наклона плоскости к горизонту 60°. Вес лебедки Q=2,4 кН, ее центр тяжести находится на прямой CO; лебедка опирается в точке A на гладкий пол, а в точке B прикреплена к полу болтом. Найти опорные реакции, пренебрегая расстоянием веревки от плоскости.

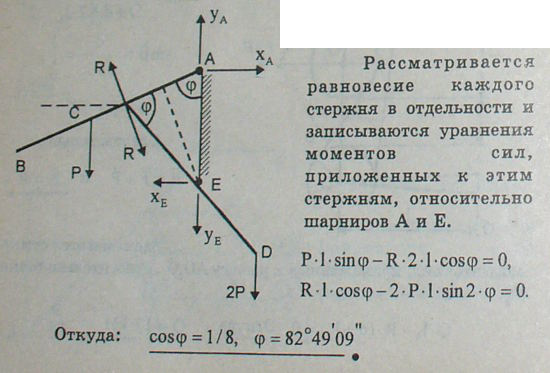
4.53 Однородный стержень AB длины 2l и веса P может вращаться вокруг горизонтальной оси на конце A стержня. Он опирается на однородный стержень CD той же длины 2l, который может вращаться вокруг горизонтальной оси, проходящей через его середину E. Точки A и E лежат на одной вертикали на расстоянии AE=l. К концу D подвешен груз Q=2P. Определить угол φ, образуемый стержнем AB с вертикалью в положении равновесия, пренебрегая трением.

4.54 Два однородных стержня AB и AC опираются в точке A на гладкий горизонтальный пол и друг на друга по гладким вертикальным плоскостям, а в точках B и C на гладкие вертикальные стены. Определить расстояние DE между стенами, при котором стержни находятся в положении равновесия, образуя друг с другом угол в 90°, если дано: длина AB равна a, длина AC равна b, вес AB равен P1, вес AC равен P2.

4.55 Однородный брусок AB, который может вращаться вокруг горизонтальной оси A, опирается на поверхность гладкого цилиндра радиуса r, лежащего на гладкой горизонтальной плоскости и удерживаемого нерастяжимой нитью AC. Вес бруска 16 Н; длина AB=Зr, AC=2r. Определить натяжение нити T и силу давления бруска на шарнир A.

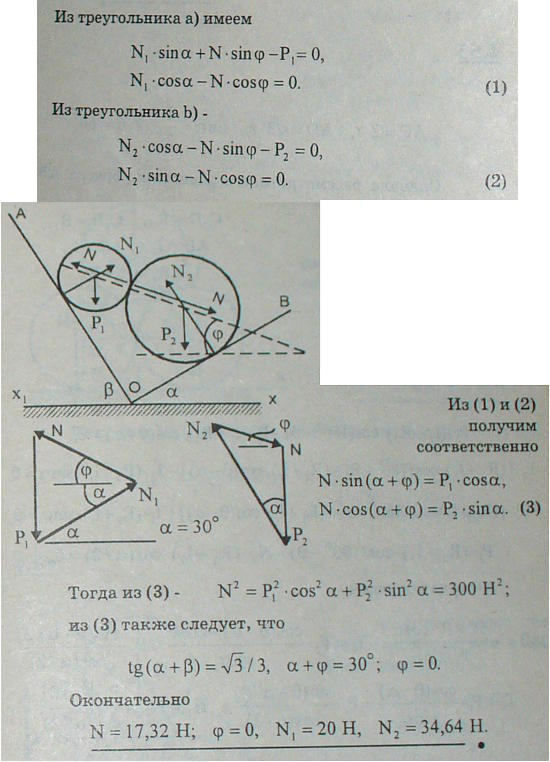
4.56 Между двумя гладкими наклонными плоскостями OA и OB положены два гладких соприкасающихся однородных цилиндра: цилиндр с центром C1 веса P1=10 Н и цилиндр с центром C2 веса P2=30 Н. Определить угол φ, составляемый прямой C1C2 с горизонтальной осью xOx1, давления N1 и N2 цилиндров на плоскости, а также силу N взаимного давления цилиндров, если угол AOx1=60°, а угол BOx=30°.

4.57 Два гладких однородных шара C1 и C2, радиусы которых R1 и R2, а веса P1 и P2, подвешены на веревках AB и AD в точке A; AB=l1; AD=l2; l1+R1=l2+R2; угол BAD=α. Определить угол θ, образуемый веревкой AD с горизонтальной плоскостью AE, натяжения веревок T1, T2 и силу давления одного шара на другой.

4.58 На двух одинаковых круглых однородных цилиндрах радиуса r и веса P каждый, лежащих на горизонтальной плоскости и связанных за центры нерастяжимой нитью длины 2r, покоится третий однородный цилиндр радиуса R и веса Q. Определить натяжение нити, давление цилиндров на плоскость и взаимное давление цилиндров. Трением пренебречь.

4.59 Три одинаковых трубы веса M=120 Н каждая лежат, как указано на рисунке. Определить давление каждой из нижних труб на землю и на удерживающие их с боков стенки. Трением пренебречь.

4.61 Механизм робота-манипулятора представляет собой шарнирный трехзвенник; звенья поворачиваются в вертикальной плоскости. Найти моменты сил приводов в шарнирах A и B механизма робота-манипулятора, необходимые для того чтобы удерживать звенья механизма в горизонтальном положении. Масса объекта манипулирования mC=15 кг. Длины звеньев: l1=0,7 м, l2=0,5 м. Звенья однородные и их массы соответственно равны: m1=35 кг, m2=25 кг.

4.62 Найти моменты сил приводов в шарнирах механизма робота-манипулятора, находящегося в равновесии, когда второе звено поднято под углом 30° к горизонту. Масса объекта манипулирования mC=15 кг. Длины звеньев: l1=0,7 м, l2=0,5 м. Массы звеньев: m1=35 кг, m2=25 кг.

4.63 Механизм робота-манипулятора в положении равновесия расположен в вертикальной плоскости. Длины звеньев: l1=0,8 м, l2=0,5 м, l3=0,3 м. Массы звеньев: m1=40 кг, m2=25 кг, m3=15 кг. Найти моменты сил приводов в шарнирах, если рука CD манипулятора несет груз, масса которого mD=15 кг. Звенья считать однородными стержнями.

4.64 Рука механизма робота-манипулятора удерживает в равновесии груз, масса которого mD=15 кг. Пружина разгрузочного устройства, предназначенного для уменьшения нагрузки на привод, действует на первое звено силой F=3000 Н, приложенной на расстоянии AE=0,2 м от шарнира A. Найти моменты сил в шарнирах. Длины звеньев: l1=0,8 м, l2=0,5 м, l3=0,3 м. Массы звеньев: m1=40 кг, m2=25 кг, m3=15 кг. Звенья считать однородными стержнями.