Два груза, в 10 Н и 5 Н, висящие на одной веревке, укреплены на ней в разных местах, причем больший груз висит ниже меньшего. Каково натяжение веревки, если верхний конец ее прикреплен к неподвижной точке?
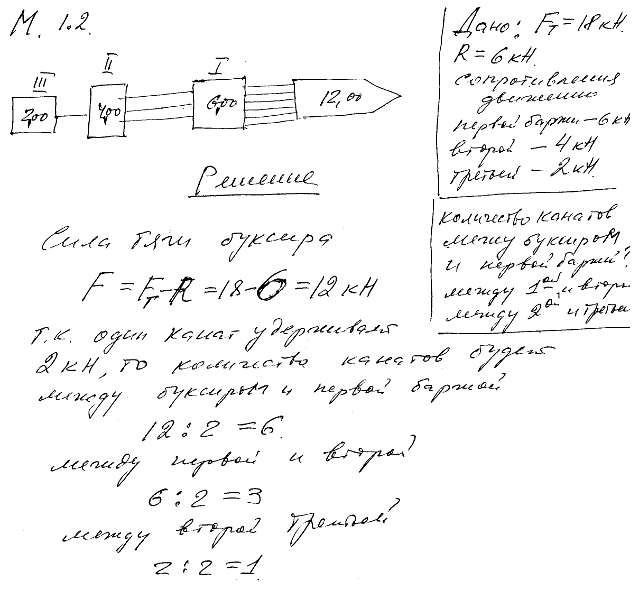
Буксир тянет три баржи различных размеров, следующие одна за другой. Сила тяги винта буксира в данный момент равна 18 кН. Сопротивление воды движению буксира равно 6 кН; сопротивление воды движению первой баржи — 6 кН, второй баржи — 4 кН и третьей — 2 кН. Имеющийся в распоряжении канат выдерживает безопасно растягивающую силу в 2 кН. Сколько канатов надо протянуть от буксира к первой барже, от первой ко второй и от второй к третьей, если движение — прямолинейное и равномерное?
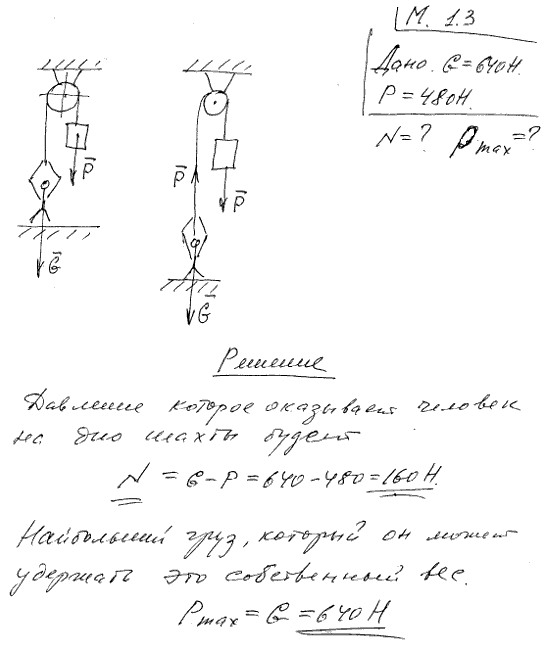
На дне шахты находится человек веса 640 Н; посредством каната, перекинутого через неподвижный блок, человек удерживает груз в 480 Н.
1) Какое давление оказывает человек на дно шахты?
2) Какой наибольший груз он может удержать с помощью каната?
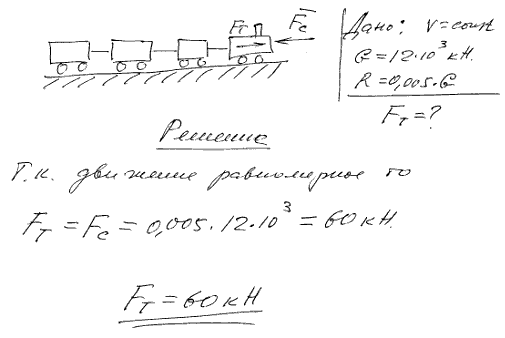
Поезд идет по прямолинейному горизонтальному пути с постоянной скоростью; вес поезда, не считая электровоза, 12*103 кН. Какова сила тяги электровоза, если сопротивление движению поезда равно 0,005 давления поезда на рельсы?
Пассажирский поезд состоит из электровоза, багажного вагона веса 400 кН и 10 пассажирских вагонов веса 500 кН каждый. С какой силой будут натянуты вагонные стяжки и какова сила тяги электровоза, если сопротивление движению поезда равно 0,005 его веса? При решении задачи принять, что сопротивление движению распределяется между составом поезда пропорционально весу и что движение поезда равномерное.
В центре правильного шестиугольника приложены силы 1, 3, 5, 7, 9 и 11 Н, направленные к его вершинам. Найти величину и направление равнодействующей и уравновешивающей.
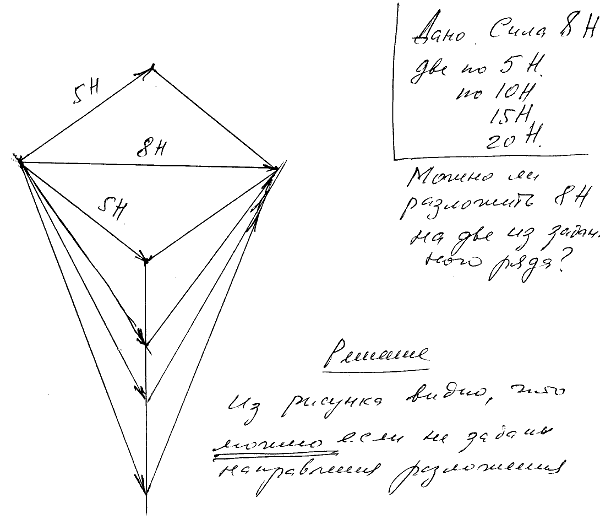
Силу в 8 Н разложить на две по 5 Н каждая. Можно ли ту же силу разложить на две по 10 Н, 15 Н, 20 Н и т.д.? На две по 100 Н?
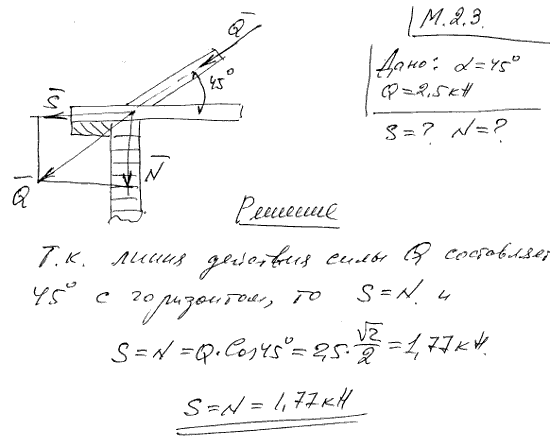
По направлению стропильной ноги, наклоненной к горизонту под углом α=45°, действует сила Q=2,5 кН. Какое усилие S возникает при этом по направлению горизонтальной затяжки и какая сила N действует на стену по отвесному направлению?
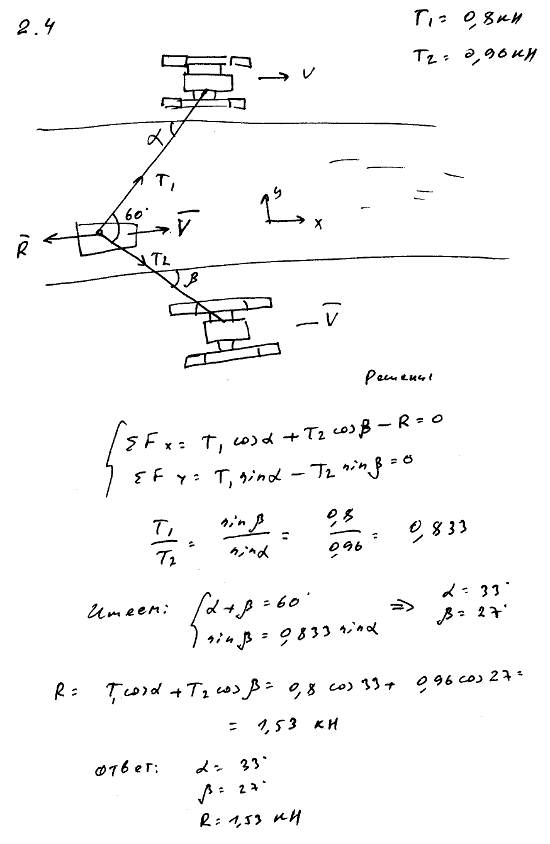
Два трактора, идущих по берегам прямого канала с постоянной скоростью, тянут барку при помощи двух канатов. Силы натяжения канатов равны 0,8 кН и 0,96 кН; угол между ними равен 60°. Найти сопротивление воды P, испытываемое баркой при ее движении, и углы α и β, которые должны составлять канаты с берегами канала, если барка движется параллельно берегам.
Кольца A, B и C трех пружинных весов укреплены неподвижно на горизонтальной доске. К крючкам весов привязаны три веревки, которые натянуты и связаны в один узел D. Показания весов: 8, 7 и 13 Н. Определить углы α и β, образуемые направлениями веревок, как указано на рисунке.
Стержни AC и BC соединены между собой и с вертикальной стеной посредством шарниров. На шарнирный болт C действует вертикальная сила P=1000 Н.
Определить реакции этих стержней на шарнирный болт C, если углы, составляемые стержнями со стеной, равны: α=30° и β=60°.
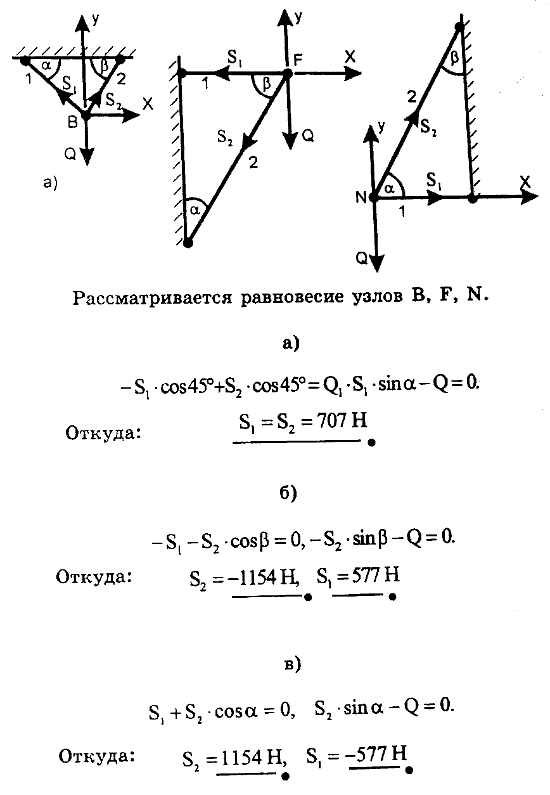
2.7 На рисунках а, б и в, как и в предыдущей задаче, схематически изображены стержни, соединенные между собой, с потолком и стенами посредством шарниров. К шарнирным болтам B, F и K подвешены грузы Q=1000 Н.
Определить усилия в стержнях для случаев: а) α=β=45°; б) α=30°, β=60°; в) α=60°, β=30°.
2.8 Уличный фонарь подвешен в точке B к середине троса ABC, прикрепленного концами к крюкам A и C, находящимся на одной горизонтали. Определить натяжения T1 и T2 в частях троса AB и BC, если вес фонаря равен 150 Н, длина всего троса ABC равна 20 м и отклонение точки его подвеса от горизонтали BD=0,1 м. Весом троса пренебречь.
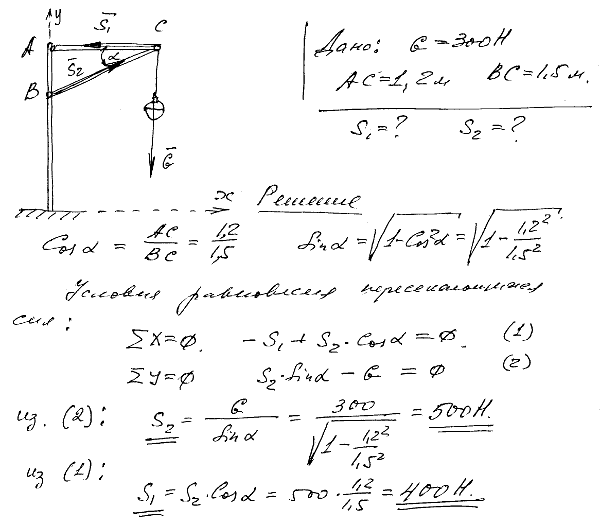
2.9 Уличный фонарь веса 300 Н подвешен к вертикальному столбу с помощью горизонтальной поперечины AC=1,2 м и подкоса BC=1,5 м. Найти усилия S1 и S2 в стержнях AC и BC, считая крепления в точках A, B и C шарнирными.
2.10 Электрическая лампа веса 20 Н подвешена к потолку на шнуре AB и затем оттянута к стене веревкой BC. Определить натяжения: TA шнура AB и TC веревки BC, если известно, что угол α=60°, а угол β=135°. Весом шнура и веревки пренебречь.
2.11 Мачтовый кран состоит из стрелы AB, прикрепленной шарниром A к мачте, и цепи CB. К концу B стрелы подвешен груз P=2 кН; углы BAC=15°, ACB=135°. Определить натяжение T цепи CB и усилие Q в стреле AB
2.12 На одной железной дороге, проведенной в горах, участок пути в ущелье подвешен так, как показано на рисунке. Предполагая подвеску AB нагруженной силой P=500 кН, найти усилия в стержнях AC и AD.
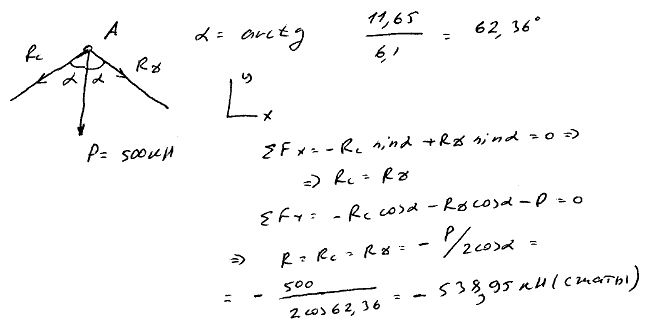
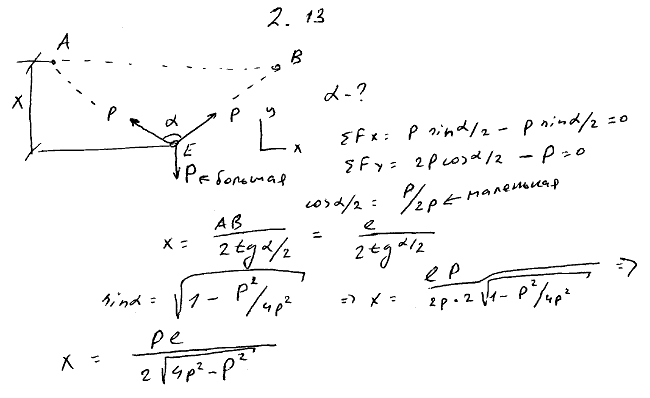
2.13 Через два блока A и B, находящихся на одной горизонтальной прямой AB=l, перекинута веревка CAEBD. К концам C и D веревки подвешены гири веса p каждая, а к точке E — гиря веса P. Определить, пренебрегая трением на блоках и их размерами, расстояние x точки E от прямой AB в положении равновесия. Весом веревки пренебречь.
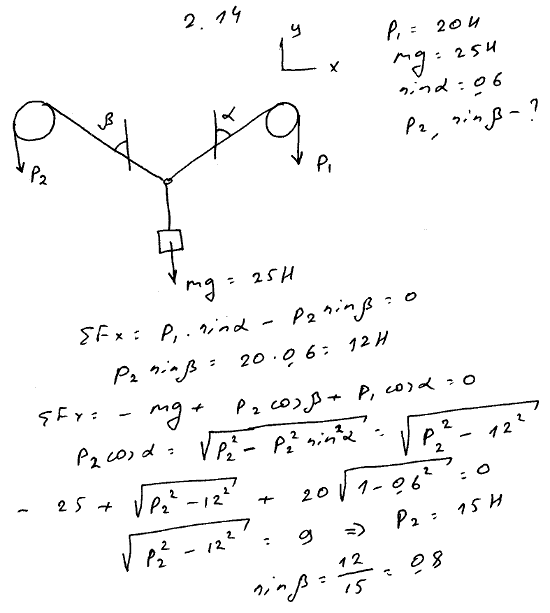
2.14 Груз веса 25 Н удерживается в равновесии двумя веревками, перекинутыми через блоки и натягиваемыми грузами. Один из этих грузов весит 20 Н; синус угла, образуемого соответствующей веревкой с вертикалью, равен 0,6. Пренебрегая трением на блоках, определить величину p второго груза и угол α, образуемый второй веревкой с вертикальной линией. Весом веревки пренебречь.
2.15 К веревке AB, один конец которой закреплен в точке A, привязаны в точке B груз P и веревка BCD, перекинутая через блок; к концу ее D привязана гиря Q веса 100 Н. Определить, пренебрегая трением на блоке, натяжение T веревки AB и величину груза P, если в положении равновесия углы, образуемые веревками с вертикалью BE, равны: α=45°, β=60°.
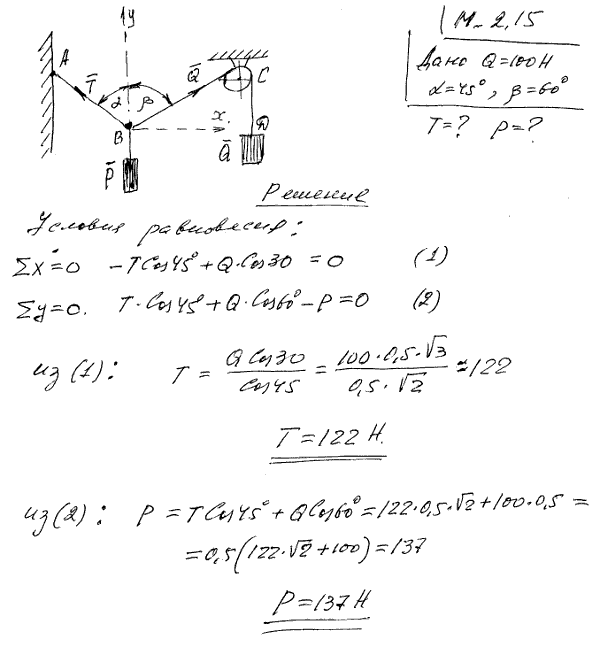
2.16 Груз P=20 кН поднимается магазинным краном BAC посредством цепи, перекинутой через блок A и через блок D, который укреплен на стене так, что угол CAD=30°. Углы между стержнями крана: ABC=60°, ACB=30°. Определить усилия Q1 и Q2 в стержнях AB и AC.
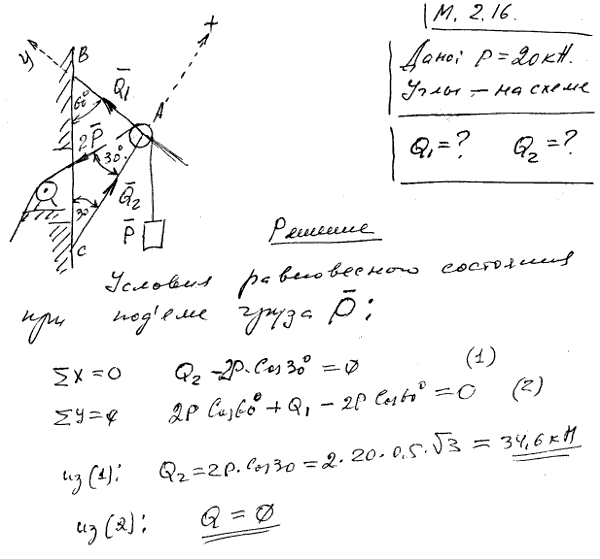
2.17 Два одинаковых цилиндра I веса P каждый подвешены на нитях к точке O. Между ними лежит цилиндр II веса Q. Вся система находится в равновесии. Цилиндры I не касаются друг друга. Определить зависимость между углом α, образованным нитью с вертикалью, и углом β, образованным прямой, проходящей через оси цилиндров I и II, с вертикалью.
2.18 На двух взаимно перпендикулярных гладких наклонных плоскостях AB и BC лежит однородный шар O веса 60 Н. Определить давление шара на каждую плоскость, зная, что плоскость BC составляет с горизонтом угол 60°.
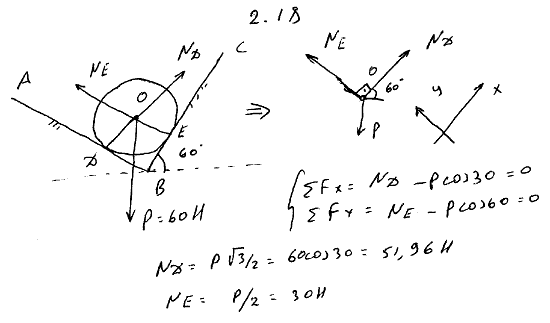
2.19 К вертикальной гладкой стене AB подвешен на тросе AC однородный шар O. Трос составляет со стеной угол α, вес шара P. Определить натяжение троса T и давление Q шара на стену.
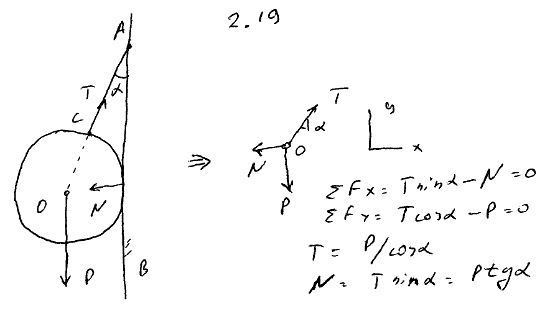
2.20 Однородный шар веса 20 Н удерживается на гладкой наклонной плоскости тросом, который привязан к пружинным весам, укрепленным над плоскостью; показание пружинных весов 10 Н. Угол наклона плоскости к горизонту равен 30°. Определить угол α, составляемый направлением троса с вертикалью, и давление Q шара на плоскость. Весом пружинных весов пренебречь.
2.21 Шарик B веса P подвешен к неподвижной точке A посредством нити AB и лежит на поверхности гладкой сферы радиуса r; расстояние точки A от поверхности сферы AC=d, длина нити AB=l, прямая AO вертикальна. Определить натяжение T нити и реакцию Q сферы. Радиусом шарика пренебречь.
2.22 Однородный шар веса 10 Н удерживается в равновесии двумя тросами AB и CD, расположенными в одной вертикальной плоскости и составляющими один с другим угол 150°. Трос AB наклонен к горизонту под углом 45°. Определить натяжение тросов.
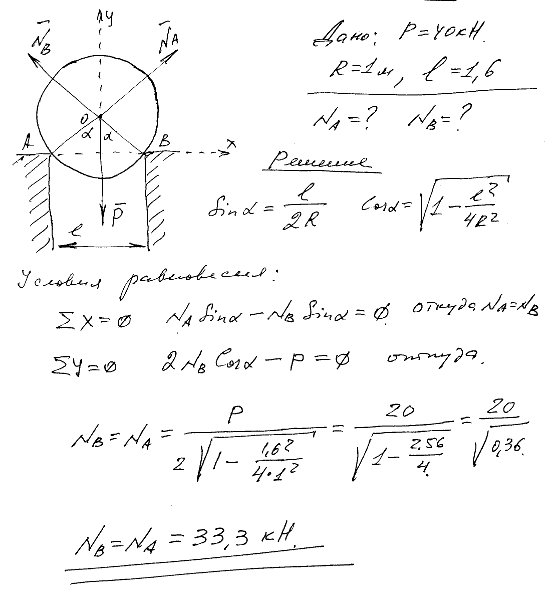
2.23 Котел с равномерно распределенным по длине весом P=40 кН и радиуса R=1 м лежит на выступах каменной кладки. Расстояние между стенками кладки l=1,6 м. Пренебрегая трением, найти давление котла на кладку в точках A и B.
2.24 Вес однородного трамбовочного катка равен 20 кН, радиус его 60 см. Определить горизонтальное усилие P, необходимое для перетаскивания катка через каменную плиту высоты 8 см, в положении, указанном на рисунке.
2.25 Однородный стержень AB веса 160 Н, длины 1,2 м подвешен в точке C на двух тросах AC и CB одинаковой длины, равной 1 м. Определить натяжения тросов.
2.26 Однородный стержень AB прикреплен к вертикальной стене посредством шарнира A и удерживается под углом 60° к вертикали при помощи троса BC, образующего с ним угол 30°. Определить величину и направление реакции R шарнира, если известно, что вес стержня равен 20 Н.
2.27 Верхний конец A однородного бруса AB, длина которого 2 м, а вес 50 Н, упирается в гладкую вертикальную стену. К нижнему концу B привязан трос BC. Найти, на каком расстоянии AC нужно прикрепить трос к стене для того, чтобы брус находился в равновесии, образуя угол BAD=45°. Найти натяжение T троса и реакцию R стены.
2.28 Оконная рама AB, изображенная на рисунке в разрезе, может вращаться вокруг горизонтальной оси шарнира A и своим нижним краем B свободно опирается на уступ паза. Найти реакции опор, если дано, что вес рамы, равный 89 Н, приложен к середине C рамы и AD=BD.
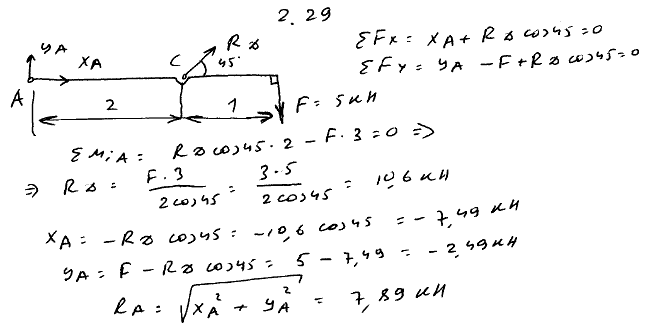
2.29 Балка AB поддерживается в горизонтальном положении стержнем CD; крепления в A, C и D шарнирные. Определить реакции опор A и D, если на конце балки действует вертикальная сила F=5 кН. Размеры указаны на рисунке. Весом пренебречь.
2.30 Балка AB шарнирно закреплена на опоре A; у конца B она положена на катки. В середине балки, под углом 45° к ее оси, действует сила P=2 кН. Определить реакции опор для случаев а и б, взяв размеры с рисунков и пренебрегая весом балки.
2.31 На рисунках изображены балки AB, удерживаемые в горизонтальном положении вертикальными стержнями CD. На концах балок действуют силы F=30 кН под углом 60° к горизонту. Взяв размеры с рисунков, определить усилия S в стержнях CD и давления Q балок на стену, если крепления в A, C и D шарнирные. Весом стержней и балок пренебречь.
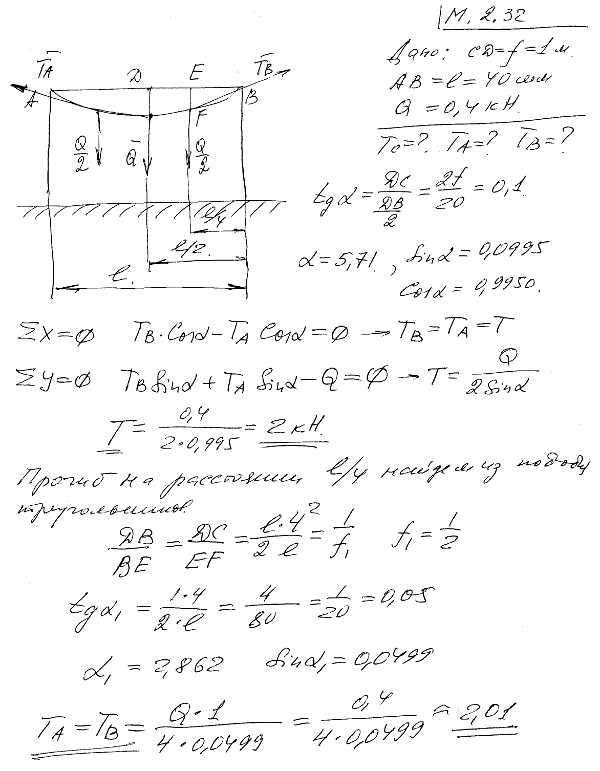
2.32 Электрический провод ACB натянут между двумя столбами так, что образует пологую кривую, стрела провисания которой CD=f=1 м. Расстояние между столбами AB=l=40 м. Вес провода Q=0,4 кН. Определить натяжения провода: TC в средней точке, TA и TB на концах.
При решении задачи считать, что вес каждой половины провода приложен на расстоянии l/4 от ближнего столба.
