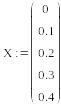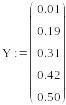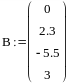Побудова графіка функції, заданої таблично.

Якщо функція у(х) задана своїми значеннями в виді таблиці:

	x	0	0,1	0,2	0.3	0,4
	y	0,01	0,19	0,31	0,42	0,50

то для побудови її графіка необхідно створити два вектори: вектор Х, заповнивши його значеннями аргумента х і вектор У, заповнивши його значеннями фнкції у.

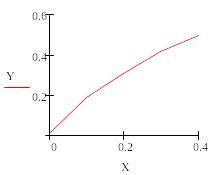
А потім, вставивши графічну область, в заповнювач під віссю х вставити вектор Х, а в заповнювач біля осі у – вектор У.

Контрольні питання:

1. Що таке плоский графік?

2. Які способи побудови плоских графіків в середовищі Mathcad ви знаєте?

3. Можливості форматування графіка.

4. Як будується графік поверхні?

Лекція № 4 Тема 1: Розв’язання системи лінійних рівнянь у програмі MathCad.

Мета роботи: Освоїти спосіб реалізації матричного методу рішення системи лінійних рівнянь в середовищі MathCAD.

Постановка задачі.

Задана система лінійних рівнянь.

Знайти розв’язок системи матричним методом в середовищі MathCAD.

Рішення системи рівнянь у матричному виді проводиться за формулою

X=A^-1B,

де:

A - матриця, що складається з коефіцієнтів при невідомих,

А^-1 - обернена матриця до матриці А,

B - вектор вільних членів,

X - вектор розвязків системи.

Приклад.

Розв’язати систему рівнянь:

7 .5x - 3y +2z -t = 0,

3x - 9.1y +z +2t = 2.3,

x + 3.1y + 7z -3t = - 5.5,

0.3x + 2.1y - 3z +8t = 3.

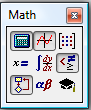
Для реалізації розрахунків в системі MathCAD необхідно скористатися панеллю інструментів Математика (Math):

,

яка визивається командою ViewToolbarsMath:

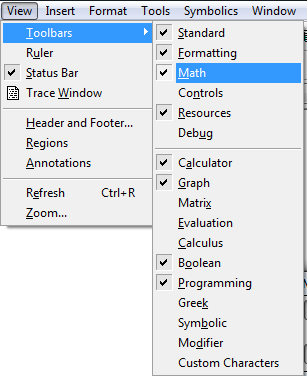
Кнопками панелі Математика необхідно визвати панелі:

• Калькулятор (кнопкою ):

• Матриця (кнопкою ):

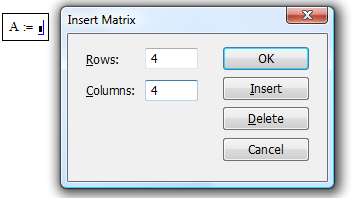
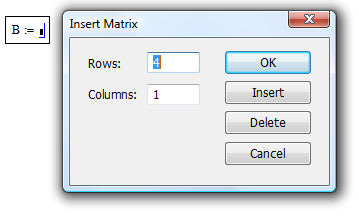
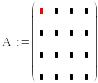
А потім виконати наступні дії: Створимо матрицю А:	Пояснення до виконуваних дій: Використавши кнопку панелі Matrix: Задаємо 4 рядки і 4 стовпці. А потім заповнюємо шаблон матриці коефіцієнтами системи:
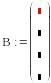
Створюємо вектор В:	Задаємо 4 рядки 1 стовпець: Після чого заповнюємо маркери шаблону значеннями вільних членів системи:
3. Обраховуємо вектор Х :	Знак присвоєння := вибираємо на панелі Calculator, обернену матрицю до матриці А створюємо за допомогою кнопки на панелі Matrix.
4. Виводимо результат розрахунків:	Результати рішення системи: x = 0.091 y = -0.243 z = -0,601 t = 0.210
5. Робимо перевірку:	Розв’язок вірний, оскільки результат перемноження матриці А на вектор Х дорівнє вектору В.