Циклічна обробка елементів вектора та матриці.

Часто виникають задачі, які потребують виконання однотипних операцій над елементами вектора або матриці. В цьому випадку доцільно однотипні операції не повторювати а «зациклити», що забеспечить їх багатократне виконання. Для цього можна використати ранжирувану змінну. Прийоми розв’язання таких задач розглянемо на прикладах.

Приклади циклічного опрацювання елементів вектора та матриці

1. Нехай заданий деякий вектор . Створити вектор В, елементами якого були би елементи вектора А, збільшені на 3.

Очевидно, що кожний елемент вектора В необхідно обчислити за формулою: b_і = 3а_і. (і = 1, 2, …,5).

Обчислення за цією формулою треба провести 5 разів, оскільки вектор А містить 5 елементів. Щоб не створювати 5 однотипних формул, можна цю формулу зациклити на п’ятикратне виконання. Для цього необхідно описати ранжовану змінну, яка буде відігравати роль індексу індексованих змінних для звернення до елементів векторів А та В:

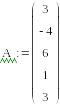
2. Створити матрицю М наступного виду: .

Раніше ми розглядали спосіб створення матриці за допомогою вставки шаблону, який треба було заповнювати елементами матриці. Тепер розглянемо інший спосіб. А саме за допомогою індексованої змінної. Оскільки для звернення до елементів матриці індексована змінна повинні мати два індекси, необхідно ввести дві ранжовані змінні: і – буде приймати значення номерів рядків і j – буде пробігати значення номерів стовпців:

і:= 1 .. 4 j:= 1 .. 4.

Далі необхідно виявити закономірності побудови елементів матриці, якщо вони є:

1. Очевидно, що в кожному рядку елементи одинакові, тобто не залежать від номеру стовпця.

2. Елементи в рядках рівні номеру рядка піднесеного до квадрату:

• в 1-му рядку елемент рівний 1² = 1,

• в 2-му рядку елемент рівний 2² = 4,

• в 3-му рядку елемент рівний 3² =6,

• в 4-му рядку елемент рівний 4² =16.

Виявивши цю закономірність, можна побудувати формулу обчислення елементів матриці:

М_{і,j =} і².

Зацикливши таку формулу, отримаємо бажаний результат.

3. Створити вектор .

Спочатку потрібно виявити закономірність в значеннях елементів вектору, тобто чи значення елементу залежить якимось чином від його номеру. Трохи помізкувавши, можна побачити, що кожний елемент дорівнює його номеру, збільшеного в 5 разів і потім ще збільшеного на 1:

6 = 51 + 1,

11 = 52 + 1,

16 = 53 +1,

21 = 54 + 1,

26 = 55 + 1.

Таким чином отримуємо формулу для обчислення елементів вектора:

Р_і = 5і + 1.

Організовуємо обчислення наступним чином:

.

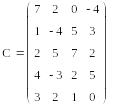
4. Задана матриця . Створити матрицю D, переставивши в матриці С перший і останній рядки.

На перший погляд здається, що для цього необхідно провести обчислення за формулами:

C_1,j = C_5,j – першому рядку матриці присвоїти елементи п’ятого рядка (де j – номер стовпця),

C_5,j = C_1,j – пятому рядку матриці присвоїти елементи першого рядка.

Але першою дією C_1,j = C_5,j ми втратимо елементи першого рядка. Тому для цього необхідно скористатись деяким проміжним вектором, наприклад Р, в якому тимчасово зберегти ці елементи:

Рj = C_1,j ,

і тільки після цього замінити елементи першого рядка елементами останнього

C_1,j = C_5,j.

А елементи останнього рядка замінити елементами першого, взявши їх з вектора Р:

C_5,j = Р.

Обчислення матимуть вигляд:
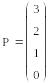