Вбудовані функції для роботи з векторами та матрицями.

Вбудовані функції можна вставити командою Вставка функції (Insert  Function), або за допомогою кнопки стандартної панелі інструментів . Після чого буде виведено вікно з переліком категорій функцій та відповідних їм імен вбудовних функцій:

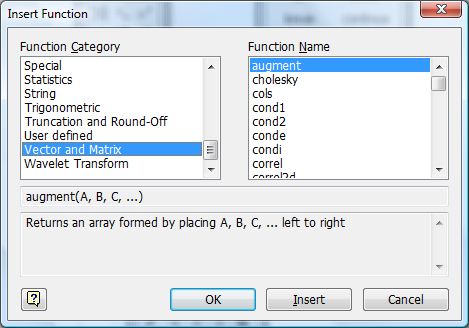
Вибравши категорію Vector and Matrix, отримаємо перелік необхідних функцій:

Назва функцій	Призначення
augment (M1, M2)	Об'єднує в одну дві матриці M1, M2, що мають однакове число рядків ( під'єднування справа)
identity(n)	створює одиничну квадратну матрицю розміром n*n
stack(M1,M2)	Об'єднує в одну дві матриці M1, M2, що мають однакове число стовпців ( під'єднування знизу)
submatrix(M, ri, rj, i,cj)	Виділяє підматрицю з матриці ri, rj – номери початкової і кінцевих рядків матриці ci, cj – номера початкового і кінцевого стовпців матриці
min(V/M)	Повертає мінімальний елемент вектора або матриці
max(V/M)	Повертає максимальний елемент вектора або матриці
rows(M)	Повертає число рядків матриці
cols(M)	Повертає число стовпців матриці
Приклади дій з матрицями

Лекція № 2

Тема: Організація циклічних обчислень.

План лекції:

1. Поняття про ранжирувану змінну. Опис ранжованої змінної.

2. Циклічна обробка елементів вектора та матриці.

3. Стандартні функції та функція користувача.

Ранжовані змінні. Основні поняття.

У математиці часто виникає необхідність в завданні ряду значень – частіше всього впорядкованого. Наприклад, ряд значень змінної (x) потрібний для побудови графіка функції. MathCad будує графіки функцій по точках, сполучаючи їх прямими. Для створення рядів значень в MathCad використовуються так звані ранжовані змінні .

Ранжована змінна – це змінна, яка приймає діапазон зміни значень. Кожне використання такої змінної сприймається, як необхідність провести обчислення по всіх її значеннях. Для створення ранжованої змінної в загальному випадку використовують вираз:

х:= а,a+h .. b,

де

х - ім'я змінної,

а - початкове значення змінної,

h – крок зміни значення змінної,

b - кінцеве значення змінної,

. . – символ перерахування значень, цей символ з'являється при наборі на клавіатурі символу - ;, або з набірної панелі Matrix кнопкою м .

Якщо крок зміни значення h=1, то для створення ранжованої змінної використовують вираз х:= а .. b.

Ранжовані змінні широко застосовуються для представлення функцій у вигляді таблиць виводу. Якщо після деякого виразу з ранжованою змінною втавити знак дорівнює (=), то на екрані буде виведена таблиця значень (мал. 12).

Мал. 12. Приклади опису ранжируваних змінних

Основне призначення ранжованої змінної – організація циклічних обчислень. Тобто за допомогою цієї змінної можна провести багатократне обчислення заданного виразу.

Вираз, який містить ранжовану змінну, обчислюватиметься таку кількість раз, яку кількість значень прийматиме ранжована змінна.

Тобто, якщо ми описали ранжовану змінну i:= 1 .. 5, а потім її використали в певному виразі, наприклад:

і+2 ,

то вставивши знак дорівнює (=) після цього виразу (команду обчислити вираз), отримаємо 5 значень виразу:

Приклад.

Протабулювати функцію, тобто обрахувати значення функції f(x) = х² + 2х -3 на відрізку [0 ; 1] в рівновіддалених точках на відстані 0,05.

Очевидно, що для обрахунку необхідно мати координати точок заданого відрізку, які відіграватимуть роль необхідних значень аргументу х функції f(x) .

Обчислення цих значень можна організувати, використавши ранжовану змінну:

х:= 0, 0+0.05 .. 1

Реалізація обрахунку матиме вид: