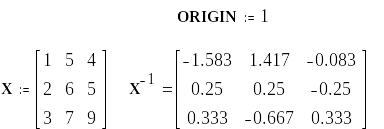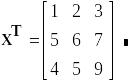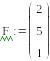3.3. Масиви

Массив- набір однотипних змінних, що мають загальне ім'я і що розрізняються між собою своїми номерами ( індексами).

Ім'я масиву утворюється також як і ім'я змінної.

MathCad працює з масивами:

вектор – (одновимірний масив, місцеположення елементу задається одним індексом);
матриця – (двовимірний масив, місцеположення елементу задається двома індексами ).

Змінні, складові масиву називаються елементами масиву.

Для створення масиву та опрацювання елементів масиву викову ристовується панель інструментів Матриці.

Приклади.

Створити вектор з пяти елементів.

Для цього іменуємо вектор ідентифікатором А, вставляємо знак привласнення (:=) і клацаємо кнопку на панелі Матриці. В вікні Вставити Матрицю вказуємо кількість рядків (5) і кількість стовпців (1):

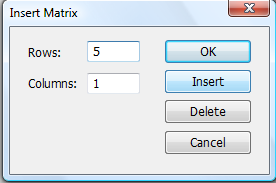
Далі отримаємо шаблон вектора :

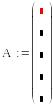
, який заповнюємо значеннями елементів вектора:

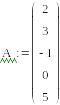
Аналогічно створюється матриця.

Для того щоб провести розрахунки над елементами вектора або матриці необхідно звертатися до їх окремих елементів. Звернення до елементів вектора або матриці проводиться за допомогою індексованої змінної.

Індексована змінна складється з імені вектора (матриці) і індексу – одного для вектора і двох для матриці. Для того щоб добавити індекс необхідно скориставтися кнопкою на панелі Матриці. Якщо наприклад необхідно змінній d присвоїти деякий елемент вектора А, то необхідно:

Після чого вказуємо номер елемента:

Командою (=) виводимо значення змінної d і бачимо, що d присвоєно значення -1, тобто значення елементу, який знаходиться на третьому місці в векторі А. Все вірно. За замовчуванням нумерація елементів вектора розпочинається з нуля. Тому значення -1 має номер 2.

Для звернення до елементів матриці необхідно вказати два індекси, які відділяються комою (,). Наприклад:

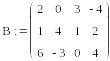
Змінній с присвоєно значення елементу матриці В, який розташований в другому рядку і першому стовпці.

Причому знову ж таки нумераці номерів рядків і стовпців розпочинається з нуля. Якщо потрібно змінити початок нумерації, то, використовується так звана попередньо визначена змінна ORIGIN (її імя складається виключно з великих букв).

Якщо задати змінній ORIGIN значення 1, то отримаємо:

Окрім вибору окркмих елементів можна також міняти значення елементів вектора або матриці:

Як бачимо значення 0 замінено на значення 8.

Робота з векторами і матрицями.

При роботі з матрицями доводиться застосовувати такі операції, як складання (віднімання) з константою, множення матриць на константу, множення матриці на вектор і так далі.

Для роботи з векторами і матрицями Система MathCad містить ряд операторів і функцій.

Ділення всіх елементів вектора а на скаляр.
Ділення матриці В на скаляр.
Створення матриці X і обернення матриці. Команда на панелі Матриці. Оберненою матрицею називається X^-1, добуток якої на задану матрицю X дає одиничну матрицю.
Транспонування матриці X. Командою на панелі Матриці. Транспонованою матрицею X^Т називається квадратна матриця, у якої стовпці відповідають рядкам квадратної матриці X
Виділення n-го стовпця матриці X Командою .
Обчислення визначника. Командою .
Обчислення суми елементів вектора. Командою на панелі Матриці.