Лекція №6 Тема: Розв’язання задаx оптимізації.

План:

1. Задача одновимірної оптимізації і її рішення.

2. Задача багатовимірної оптимізації і її рішення.

Завдання оптимізації.

Основною метою вирішення завдань управління системою є досягнення деякого оптимального режиму роботи. Багато досліджуваних процесів вимагають оптимізації. Під оптимізацією мають на увазі знаходження max або min функції. Завдання оптимізації діляться на:

• - завдання одновимірної оптимізації

• - завдання багатовимірної оптимізації.

Одновимірна оптимізація розглядає функції, залежні від однієї змінної.

Багатовимірна оптимізація розглядає функції, залежні від багатьох змінних.

Задача одновимірної оптимізації.

Постановка завдання:

Дана функція y=f(x)

Потрібно визначити мінімальне значення функції min f(x)

Методи мінімізації дозволяють визначити точку мінімуму функції, тобто таке значення x*, при якому функція досягає min значення . f_min=((x*). При цьому задається точність, яка визначає наближене значення точки мінімуму функції.

Ця задача розвязується в два етапи:

1. Графічним методом проводиться пошук початкового значення точки мінімума.

Для цього необхідно побудувати графік функції f(x).

Проаналізувати чи має вона мінімум і, якщо так,

то з графіку наближено визначити при якому значенні аргументу х

цей мінімум досягається.

2. Потім початкове значення точки мінімума уточнюється до заданого ступена точності .

У MathCad цю задачу можна вирішити за допомогою вирішального блоку. У тілі блоку записуємо необхідну умову екстремуму функції, що диференціюється.

Приклад.

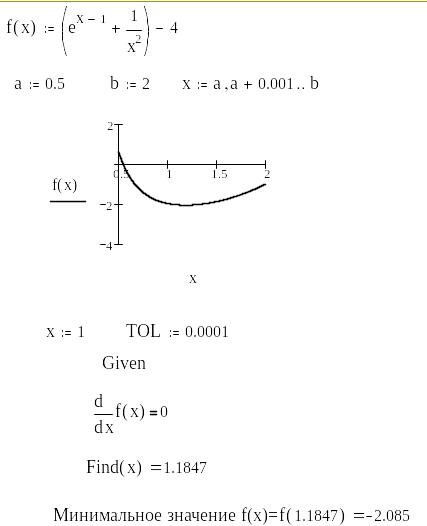
Знайти мінімальне значення функції

Функція має мінімум на відрізку ( 0,5; 2)

Рішення задачі багатовимірної оптимізації.

Багато інженерних завдань зводяться до знаходження мінімуму або максимуму функції декілька змінних. Основною метою вирішення завдань управління деякими галузями промисловості зазвичай є досягнення деякого оптимального режиму роботи. У цих випадках вирішення таких завдань моделюється знаходженням оптимуму функції декілька змінних.

Розглянемо рішення даної задачі на прикладі функції два змінних.

Постановка завдання.

Хай задана функція z=f(x, у). Потрібно знайти мінімальне або максимальне значення даної функції. Дане завдання вирішується приблизно. Причому заздалегідь потрібно визначити точку мінімуму (x*,y*) з точністю (, а потім значення в крапці мінімуму і буде шукане оптимальне значення функції. Метод рішення вимагає попереднього визначення початкових значень точки мінімуму (x0,y0). Початкові значення можна визначити графічно. Для цього потрібно в деякій області на плоскості XOY побудувати графік функції z=f(x, у).

Розглянемо рішення даної задачі на конкретному прикладі.

Задана функція

.

Потрібно визначити координати початкової точки мінімуму. Функція нелінійна і її графічною інтерпретацією є якась поверхня в тривимірному просторі. Побудуємо графік даної функції в деякій прямокутній області на плоскості Хоy, яку визначимо двома інтервалами по осі OX і OY відповідно: (а, b) і (з, d). У даній області потрібно визначити координати крапок, по яких буде побудований графік початкової функції. Для цього інтервали (а, b) і (з, d) розіб'ємо на n частин і створимо вектора X, Y, що містять координати x, у всіх точок області.

Опишемо задану функцію як функцію користувача.

Створимо матрицю Z, що містить значення функції в точках певної області.

Викликаємо графічну область для побудови графіків поверхонь за допомогою команди Insert(Graph(Surface Plot.

У область індикатора потрібно ввести ім'я матриці Z. Після форматування графік поверхні прийме вигляд:

Графік поверхні дозволяє визначити тільки якісну поведінку функції, але не кількісне. Очевидно, що функція має точку екстремуму – точку мінімуму. Щоб кількісно оцінити положення цієї крапки на плоскості необхідно побудувати контурний графік.

Графік поверхні можна перетворити в контурний графік (Contour Plot), на якому представлена безліч ліній рівня функції z(x,y). При побудові контурного графіка необхідно потім у вікні форматування задати координати інтервалів по осі OX і OY, які визначили область побудови графіка.

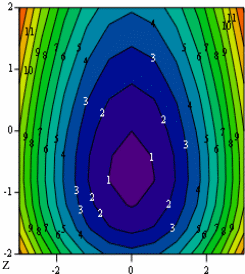
На лініях рівня виведені значення функції, яких досягає функція в точках кожної з ліній. Очевидно, що точка мінімуму знаходиться в самій внутрішній замкнутій лінії.

Тому початкове наближення координат точки мінімуму можна вибрати рівне:

Для уточнення координат точки мінімуму застосуємо функцію мінімізації minimize:

- координати точки мінімуму.

Підставляючи координати точки мінімуму в початкову функцію, визначаємо мінімальне значення функції zmin.

Контрольні питання:

1. Що є завдання оптимізації?

2. У чому полягає постановка завдання одновимірної і багатовимірної оптимізації?

3. Як можна знайти мінімум функції однієї змінної в середовищі Mathcad?

4. Як вирішується завдання багатовимірної оптимізації в середовищі Mathcad

41