4. Суждение

Суждение – норма мышления, в которой что-либо утверждается или отрицается о существовании предметов, связях между предметом и его свойствами или об отношении между предметами.

Если то, о чем говорится в суждении, соответствует действительному положению вещей, то суждение истинно. Традиционная логика является двузначной, так как в ней суждение имеет одно из 2-х значений истинности: оно либо истинно, либо ложно. В трехзначных логиках суждение может быть либо истинным, либо ложным, либо неопределенным. Так, многие суждения о будущих единичных событиях являются неопределенными. Об этом писал еще Аристотель: «Завтра необходимо будет морское сражение».

А) Простые суждения

Простым называется суждение, в котором нельзя выделить правильную часть, т.е. часть, не совпадающую с целым, в свою очередь, являющуюся суждением.

Среди простых суждений выделяют (1) атрибутивные суждения и (2) суждения об отношениях.

Атрибутивные суждения – это суждения, в которых выражается принадлежность предметам или отсутствие у предметов каких – либо свойств («Мед сладкий», «Шопен не является драматургом»).

(«S» есть «P» или «S» не есть «P»).

В каждом атрибутивном суждении есть субъект (логическое подлежащее), предикат (логическое сказуемое) и связка (связка иногда лишь подразумевается) а в некоторых имеются кванторные (количественные) слова («некоторые», «все», «ни один» и др.)

Субъект («S») и предикат («Р») называются терминами суждения.

Пример: «Некоторые (- кванторное слово) науки («S») не являются (- связка) гуманитарными («P»).

Атрибутивные суждения делятся на виды:

- «по количеству»: единичные, общие, частные,

- «по качеству»: утвердительные, отрицательные.

В утвердительных атрибутивных суждениях выражается полное или частичное включение класса предметов в класс предметов или же принадлежность некоторого предмета к классу предметов.

В отрицательных - выражается невключение класса предметов, части класса, предмета в некоторый класс предметов. («Иванов не является юристом», «Сидоров является юристом»).

В единичных суждениях выражается принадлежность или непринадлежность предмета классу предметов. («Москва – столица Российской Федерации»).

В общих – включение или невключение класса предметов в класс. («Все сделки, не соответствующие требованиям закона, являются не действительными»).

В частных суждениях – выражается частичное включение или невключение в класс предметов. («Некоторые преступления не являются преднамеренными»).

При решении вопроса о правильности и неправильности рассуждений и в некоторых других случаях используется так называемое объединенное деление атрибутивных суждений по качеству и количеству:

Общеутвердительные – суждения, которые одновременно и общие, и утвердительные. Структура: «Все S суть P», обозначается: А.

Общеотрицательные – являются одновременно и общими, и отрицательными. Структура: «Ни одно S не суть P», обозначается: E.

Частноутвердительное - является одновременно частным и утвердительным. Структура: «Некоторые S суть P», обозначается: I.

Частноотрицательное - является одновременно и частным, и отрицательным. Структура: «Некоторые S не суть P», обозначается О.

Б) Распределенность терминов в категорически суждениях

Так как простое суждение состоит из терминов S и P, которые являются понятиями, могут рассматриваться со стороны объема, то любое отношение между S и P в простых суждениях может быть изображено при помощи круговых схем Эйлера, отражающих отношения между понятиями.

В суждениях термины S и P могут быть распределены, либо не распределены. Термин считается распределенным, если его объем полностью включается в объем другого термина или частично исключается из него.

А («Все S суть P») ® истинно при следующих отношениях между S и P:

S – распределен Объем S полностью распределен

P – распределен,

т.к. их объемы

полностью совпадают

Если P > S, то P не распределен.

Суждение I («Некоторые S суть P»): «Некоторые юристы – спортсмены».

Т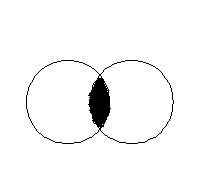 ермины: S – «юристы»;

P – «спортсмены»;

Кванторные суждения – «некоторые».

S – не распределен, так как в нем мыслится часть

S P юристов, т.е. объем субъекта лишь частично включается

в объем предиката и наоборот.

Если понятия S и P перекрещиваются, то P не распределен.

Субъект не распределен, т.к. в нем мыслится только часть

писателей. Предикат распределен, ибо объем предиката

полностью входит в объем субъекта.

Т.о. P распределен, если объем P < объема S, что бывает в

частных выделяющихся суждениях.

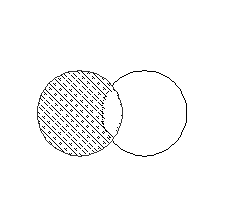
E («Ни одно S не суть P»): «Ни один юрист не есть шахтер»

Объем S и P не распределены, так как объем S исключается из объема P.

Суждение О («Некоторые S не суть P»): «Некоторые юристы не являются адвокатами». Субъект не распределен¹².

P S P

Итак, S распределен в общих суждениях и не распределен в частных; P всегда распределен в отрицательных суждениях, в утвердительных же он распределен тогда, когда по объему P £ S.

Распределенный термин «+»,

нераспределенный «-».

«Все S⁺ суть P ^-»; «Ни одно S⁺ не суть P^-»; «некоторые S^- суть P^-»; «некоторые S^- не суть P⁺».

Суждения об отношениях

– это суждения, в которых говорится о том, что определенное отношение имеет место (или не имеет места) между элементами пар, троек, и т.д. предметов.

Они делятся на:

Утвердительные – в них говорится о том, что предметы находятся в определенном отношении.

В отрицательных суждениях сообщается о том, что предметы не находятся в определенном отношении.

«Каждый следователь знает некоторого адвоката лучше, чем некоторого прокурора».

«Некоторые студенты нашей группы не знают некоторых чемпионов мира».

В) Сложные суждения

Сложные суждения образуются из простых суждений с помощью логических связок: конъюнкции, дизъюнкции, импликации, эквиваленции и отрицания.

Таблица истинности этих логических связок:

а	в	аÙв	аÚв	а ύ в	а®в	а º в
И	И	И	И	Л	И	И
И	Л	Л	И	И	Л	Л
Л	И	Л	И	И	И	Л
Л	Л	Л	Л	Л	И	И

Конъюнкция аÙв – истинна, если а – истинна и в - истинна.

Нестрогая дизъюнкция аÚв – истинна, если истинно хотя бы одно суждение; ложна, если ложны оба суждения.

Строгая дизъюнкция а ύ в – в которой члены дизъюнкции исключают друг друга. Истинна тогда, когда лишь одно из 2-х простых суждений истинно, и только одно.

Импликация - а®в истинна всегда, кроме 1 случая, когда первое суждение истинно, а второе ложно.

Эквиваленция а º в истинна в тех и только в тех случаях, когда и а, и в либо оба истинны, либо оба ложны.

Тождественно-истинной формулой называется формула, которая при любых комбинациях значений для входящих в неё переменных принимает значение «истина».

Тождественно-ложная формула – та, которая принимает только значение «ложь».

Выполнимая формула может принимать значение как «истина», так и «ложь».

Тождественно-истинная, и тождественно-ложная, и выполнимая формулы состоят из 3 и более переменных.

Виды сложных суждений

Соединительные суждения – это суждения, в которых утверждается наличие двух или более ситуаций.

Пример: «Понятые присутствуют, и протокол составляется». Чаще всего такие утверждения выражаются посредством предложений, содержащих союз «и».

Примеры: «Идет дождь и идет снег», или «Я вышел на улицу и сломал ногу».

Союз «И» обозначается символом Ù (читается «и»), называемым знаком (коммутативной) конъюнкции. Суждения с этим союзом называется (коммутативно) конъюнктивным.

Форма конъюнктивного суждения:

(А ÙВ)

Таблица истинности:

А	В	А ÙВ
И	И	И
И	Л	Л
Л	И	Л
Л	Л	Л

Суждения, в которых утверждается последовательное возникновение или существование двух или более ситуаций, называются некоммутативно-конъюктивными. Они образуются из двух или более суждений при помощи союзов, обозначаемых символами Т₂, Т₃ и т.д. в зависимости от числа суждений, из которых они образуются. Эти знаки называются знаками некоммутативной конъюнкции: «а затем,…затем, а затем…» и т. д. Форма суждения с 2-х местным союзом Т: Т₂ (А,В), или (АТВ). Примеры: «Были приглашены понятые, а затем составлен протокол». Вместо выражения: «а затем» чаще всего употребляется союз «и». «Были приглашены понятые и был составлен протокол».

Форма суждения с 3-х местным союзом - Т: Т₃ (А,В,С). Пример: «Петров вышел на улицу, затем остановил такси, а затем направился в центр города».

Разделительные суждения – это суждения, в которых утверждается наличие одной из 2-х, 3-х и т.д. ситуаций.

Если утверждается наличие по крайней мере одной из 2-х ситуаций, суждение называется (нестрого) разделительным, или дизъюнктивным.

Если утверждается наличие ровно одной из 2-х или более ситуаций, то суждение называется строго-дизъюнктивным.

Союз: «или» применяется в дизъюнктивном; «или…, или…», «либо…либо» и т.д. в строго-дизъюнктивном.

Союз «или», посредством которого выражается утверждение 1-го типа обозначается символом Ú (читается «или») - знаком нестрогой дизъюнкции.

Союз «или…, или…» - утверждение 2-го типа, обозначается символом Ú - знаком строгой дизъюнкции.

Примеры:

А	В	АÚВ
И	И	И
И	Л	Л
Л	И	Л
Л	Л	Л

«Иванов является юристом или Иванов является спортсменом»

А	В	А Ú В
И	И	Л
И	Л	И
Л	И	И
Л	Л	Л

«Иванов совершил это преступление или Иванов не совершал этого преступления»

Знаки 2-х, 3-х и т.д. строгой дизъюнкции: Ú _2, Ú ₃ и т. д. «Или Иванов совершил это преступление, или Петров, или Сидоров».

Итак, строго-дизъюнктивное суждение, Ú _n (А1, …А_n), где n ³ 2: это суждение, которое истинно тогда и только тогда, когда истинно одно и только одно суждение из составляющих его суждений.

Условные и импликативные суждения

Суждение, в котором утверждается, что наличие одной ситуации обуславливает наличие другой, - называется условным («если…, то). Условие называется необходимым для данного события, если при его отсутствии это событие не происходит. («Наличие атмосферы является условием для возникновения на Земле существующих видов высокообразованных животных»).

Условие называется достаточным, если всякий раз, когда имеется это условие, событие происходит. («Выпадение дождя – достаточное условие для того, чтобы крыши домов были мокрыми»).

Условия могут быть: «достаточными, но не необходимыми; «необходимыми, но не достаточными» и т. д.

В условном суждении выделяют основание («антецедент») и следствие («консеквент»). Основание – та часть условного суждения, которая располагается между «если» и «то»; следствие – после «то».

Условным называется суждение, в котором ситуация, описываемая основанием, является достаточным условием для ситуации, описываемой следствием.

Союз «если…то» обозначается: ® (знаком импликации).

В построениях современной логики находит распространение «союз», если…то». Он обозначается: «É» - знаком материальной импликации, а суждение с этим союзом называется импликативным. Знак É - используется вместо слова «следовательно» в рассуждениях. Логический союз É передает общий смысл этих союзов, заключенных в определенной зависимости истинности сложного суждения от истинности составляющих.

Суждения эквивалентности и материальной эквивалентности

Суждения эквивалентности - это суждение, в котором утверждается взаимная обусловленность 2-х ситуаций. Союзы – «если и только если…, то…» («тогда и только тогда…, когда…»).

Основание в этих суждениях выражает достаточное и необходимое условие для ситуации, описываемой следствием. Следствие – также является достаточным и необходимым условием для события, описываемого основанием.

А	В	А º В
И	И	И
И	Л	Л
Л	И	Л
Л	Л	И

Суждение с союзом «если и только если…, то…» - суждение материальной эквивалентности.

Суждение с внешним отрицанием

– суждение, в котором утверждается отсутствие некоторой ситуации.

Словосочетание: «неверно, что», обозначается «ù » - знаком отрицания.

А	ù А
И	Л
Л	И

Особенно важно различать союзы Ù, T, Ú, Ú и т.д. в документах, имеющих юридическое значение.¹³